Властивості логічного слідування
- Якщо
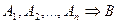 і
і 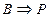 , то
, то 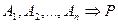 (властивість транзитивності).
(властивість транзитивності). - Якщо
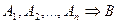 і Р – довільна формула алгебри висловлень, то
і Р – довільна формула алгебри висловлень, то
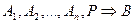 (приєднання довільної формули алгебри висловлень до числа посилок не порушує даного логічного слідування).
(приєднання довільної формули алгебри висловлень до числа посилок не порушує даного логічного слідування).
- Якщо
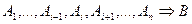 і
і 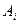 є тавтологією, то
є тавтологією, то
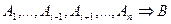 (вилучення з числа посилок формули, яка є тавтологією, не порушує даного логічного слідування)
(вилучення з числа посилок формули, яка є тавтологією, не порушує даного логічного слідування)
Схеми логічного слідування (правила виведення) в логіці висловлювань
8. Modus ponens (МР) (правило висновку): p 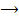 q, p
q, p 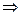 q
q
(Modus– лат. спосіб , ponens – що стверджує);
“Якщо з висловлення p прямує висловлення q і висловлення p істинно, то істинно і q ”.
9. Modus tollens (МТ): p 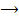 q,
q, 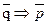 (tollens - заперечувальний)
(tollens - заперечувальний)
10. Введення диз’юнкції: p 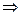 p
p 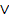 q;
q;
Похолоднішало.Отже похолоднішало, або почав падати дощ.
11. Вилучення кон’юнкції: p, q 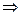 p;
p;
Похолоднішало і почав падати дощ, отже похолоднішало.
12. Правило силогізму: p 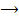 q, q
q, q 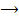 r
r 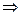 p
p 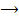 r;
r;
Якщо сьогодні падатиме дощ, то сьогодні ми не поїдемо на пікнік.
Якщо ми не поїдемо на пікнік сьогодні, то поїдемо завтра.
Отже, якщо сьогодні падатиме дощ, то поїдемо на пікнік завтра.
13. Диз’юнктивний силогізм: p 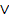 q,
q, 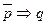 ;
;
14. Резолюція: p 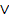 q,
q, 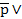 r
r 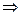 q
q 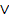 r.
r.
Множина формул 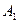 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 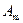 (p1,p2,...,pn), називається сумісною(несуперечною), якщо існує такий розподіл істинісних значень p1,p2,...,pn, ,
(p1,p2,...,pn), називається сумісною(несуперечною), якщо існує такий розподіл істинісних значень p1,p2,...,pn, ,
при якому 
Множина формул, яка не є сумісною, називається суперечною.
Множина формул 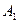 (p1,p2,...,pn), … ,
(p1,p2,...,pn), … , 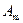 (p1,p2,...,pn), називається сумісною(суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень p1,p2,...,pn,, всі формули (хоча б одна з формул) набувають (набуває ) значення 1 (0).
(p1,p2,...,pn), називається сумісною(суперечною) тоді і тільки тоді, коли хоча б на одному наборі (на всіх наборах) значень p1,p2,...,pn,, всі формули (хоча б одна з формул) набувають (набуває ) значення 1 (0).
Теорема Якщо Г – суперечна множина формул логіки висловлювань, то для довільної формули А має місце слідування 
Дата добавления: 2016-04-22; просмотров: 877;
