Производная по направлению.
Пусть скалярное поле 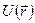 имеет в некоторой точке М0 значение U0, и пусть при перемещении
имеет в некоторой точке М0 значение U0, и пусть при перемещении 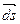 по направлению вектора
по направлению вектора 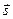 мы приходим из точки М0 в точку М, где скалярное поле имеет значение Us. Приращение U при этом перемещении равно
мы приходим из точки М0 в точку М, где скалярное поле имеет значение Us. Приращение U при этом перемещении равно 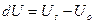 . Предел отношения этого приращения dU к численной величине перемещения ds называется производной скаляра U в точке М0 по направлению
. Предел отношения этого приращения dU к численной величине перемещения ds называется производной скаляра U в точке М0 по направлению 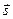 :
:
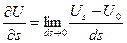
Значение этой производной существенно зависитот выбора направления 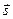 и ее ни в коем случае нельзя смешиватьс обыкновенной частной производной по скалярному параметру s. Чтобы подчеркнуть это обстоятельство, часто такую производную обозначают:
и ее ни в коем случае нельзя смешиватьс обыкновенной частной производной по скалярному параметру s. Чтобы подчеркнуть это обстоятельство, часто такую производную обозначают: 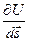
12.Градиент.
Градиентом поля 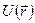 называется вектор, определяемый в каждой точке поля соотношением:
называется вектор, определяемый в каждой точке поля соотношением: 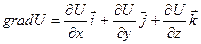
Тогда 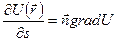 , где
, где 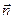 - единичный вектор в направлении
- единичный вектор в направлении 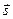 .
.
Часто вектор gradU обозначают также 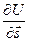 или
или 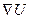 , где
, где 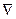 ("набла") обозначает символический вектор, называемый оператором Гамильтона или набла-оператором:
("набла") обозначает символический вектор, называемый оператором Гамильтона или набла-оператором:

13.Поток поля через поверхность.
Разобьем данную поверхность S на n элементарных площадок размером 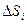 . Внутри каждой площадки выберем точку
. Внутри каждой площадки выберем точку 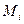 - и в этой точке построим нормальный к поверхности единичный вектор
- и в этой точке построим нормальный к поверхности единичный вектор 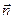 и вектор
и вектор 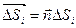 направление которого
направление которого 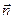 а модуль
а модуль 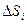 . Тогда мы определяем:
. Тогда мы определяем:
1) Поток скалярного поля: 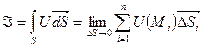
2) Скалярный поток векторного поля: 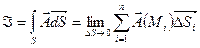
3) Векторный поток векторного поля: 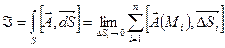
14.Производная по объему.
Под производными по объему скалярного или векторного полей в точке М понимают величины трех типов, которые получают следующим образом.
(1) Точка М окружается замкнутой поверхностью S, которая охватывает область с объемом V. (2) Вычисляется интеграл 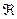 по поверхности S:
по поверхности S:

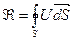 , или
, или  , или
, или 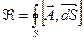 . (3) Определяется предел
. (3) Определяется предел 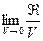
отношения этого интеграла к объему V, когда S стягивается в точку М, так что V стремится к нулю.
15. Дивергенция векторного поля.
Дивергенцией(обозначается 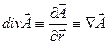 ) векторного поля
) векторного поля 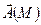 называют следующую производную по объему поля в точке М:
называют следующую производную по объему поля в точке М:
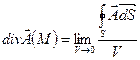
Величина 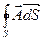 есть скалярный поток векторного полячерез замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.
есть скалярный поток векторного полячерез замкнутую поверхность S, которая окружает точку М и охватывает область G с объемом V.
Дивергенция  есть мера источников поля
есть мера источников поля 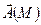 . Если в области G
. Если в области G 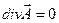 , то векторное поле
, то векторное поле 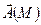 называется свободным от источников. Те точки поля, в которых
называется свободным от источников. Те точки поля, в которых 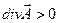 принято называть источникамиполя, а те, в которых
принято называть источникамиполя, а те, в которых 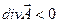 — стокамиполя. 16.Формула Гаусса-Остроградского.
— стокамиполя. 16.Формула Гаусса-Остроградского.
Для пространственной области G, ограниченной замкнутой поверхностью S:
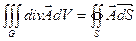
17.Оператор Лапласа.
Пусть U(M) — скалярное поле, тогда оператор Лапласа 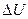 определяется следующим образом:
определяется следующим образом:
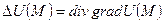
или в декартовых координатах:
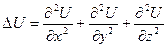
Оператор Лапласа векторного поля: 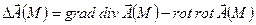
18.Ротор векторного поля.
Ротором (вихрем) векторного поля 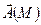 называют следующую производную по объему поля в точке М:
называют следующую производную по объему поля в точке М:
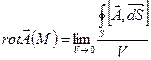
Обозначается: 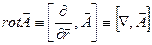
19.Теорема Стокса.
Циркуляция векторного поля 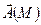 по замкнутой кривой L равна потоку ротора этого поля черезповерхность S , опирающуюся на кривую L:
по замкнутой кривой L равна потоку ротора этого поля черезповерхность S , опирающуюся на кривую L:

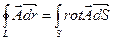
Примечание.
В этом приложении приведены определения некоторых математических понятий, часто используемых в курсе физики. Материал носит справочный характер, поскольку предполагается, что данные понятия известны читателю.

ГРЕЧЕСКИЙ АЛФАВИТ
| Прописные | Строчные | Название | Прописные | Строчные | Название | Прописные | Строчные | Название |
| Α | α | Альфа | Ι | ι | Йота | Ρ | ρ | Ро |
| Β | β | Бэта | Κ | Κ | Каппа | Σ | σ,ς | Сигма |
| Γ | γ | Гамма | Λ | Λ | Лямбда | Τ | τ | Тау |
| Δ | δ | Дэльта | Μ | Μ | Мю | Υ | Υ | И-псилон |
| Ε | ε | Э-псилон | Ν | Ν | Ню | Φ | Φ | Фи |
| Ζ | ζ | Дзэта | Ξ | ξ | Кси | Χ | Χ | Хи |
| Η | η | Эта | Ο | Ο | О-микрон | Ψ | Ψ | Пси |
| Θ | θ | Тэта | Π | Π | Пи | Ω | Ω | О-мега |
Дата добавления: 2016-04-22; просмотров: 906;
