Частная производная, полный дифференциал ФНП. Связь дифференцируемости функции с существованием частных производных
Для функции одной вещественной переменной после изучения тем «Пределы» и «Непрерывность» (Введение в математический анализ) изучались производные и дифференциалы функции. Перейдем к рассмотрению аналогичных вопросов для функции нескольких переменных. Заметим, что если в ФНП зафиксировать все аргументы, кроме одного, то ФНП порождает функцию одного аргумента, для которой можно рассматривать приращение, дифференциал и производную. Их мы будем называть соответственно частным приращением, частным дифференциалом и частной производной. Перейдем к точным определениям.
Определение 1. Пусть задана функция 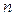 переменных
переменных 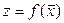 где
где 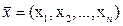 - элемент евклидова пространства и соответствующие приращения аргументов
- элемент евклидова пространства и соответствующие приращения аргументов 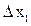 ,
, 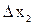 ,…,
,…, 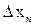 . При
. При 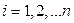 величины
величины 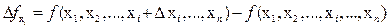 , называются частными приращениями функция
, называются частными приращениями функция 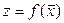 . Полное приращение функции
. Полное приращение функции 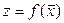 - это величина
- это величина 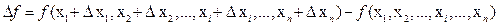 .
.
Например, для функции двух переменных 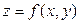 , где
, где 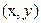 - точка на плоскости и
- точка на плоскости и 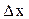 ,
, 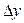 соответствующие приращения аргументов, частными будут приращения
соответствующие приращения аргументов, частными будут приращения 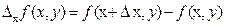 ,
, 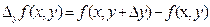 . При этом величина
. При этом величина 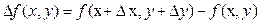 является полным приращениями функции двух переменных
является полным приращениями функции двух переменных 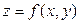 .
.
Определение 2. Частной производной функции 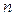 переменных
переменных 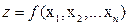 по переменной
по переменной 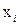 называется предел отношения частного приращения функции по этой переменной к приращению соответствующего аргумента
называется предел отношения частного приращения функции по этой переменной к приращению соответствующего аргумента 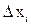 , когда
, когда 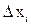 стремится к 0.
стремится к 0.
Запишем определение 2 в виде формулы 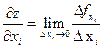 или развернуто
или развернуто 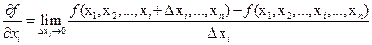 . Для функции двух переменных
. Для функции двух переменных 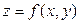 определение 2 запишется в виде формул
определение 2 запишется в виде формул 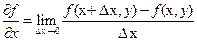 ,
, 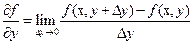 . С практической точки зрения данное определение означает, что при вычислении частной производной по одной переменной все остальные переменные фиксируются и мы рассматриваем данную функцию как функцию одной выбранной переменной. По этой переменной и берется обычная производная.
. С практической точки зрения данное определение означает, что при вычислении частной производной по одной переменной все остальные переменные фиксируются и мы рассматриваем данную функцию как функцию одной выбранной переменной. По этой переменной и берется обычная производная.
Пример 1. Для функции 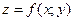 , где
, где 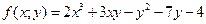 найдите частные производные и точку, в которой обе частные производные равны 0.
найдите частные производные и точку, в которой обе частные производные равны 0.
Решение. Вычислим частные производные 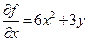 ,
,  и систему
и систему 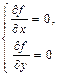 запишем в виде
запишем в виде 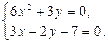 Решением этой системы являются две точки
Решением этой системы являются две точки 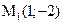 и
и 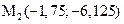 .
.
Рассмотрим теперь, как понятие дифференциала обобщается на ФНП. Функция одной переменной 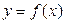 называется дифференцируемой, если ее приращение
называется дифференцируемой, если ее приращение 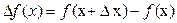 представляется в виде
представляется в виде 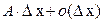 , при этом величина
, при этом величина 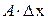 является главной частью приращения функции и называется ее дифференциалом. Величина
является главной частью приращения функции и называется ее дифференциалом. Величина 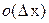 является функцией от
является функцией от 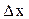 , обладает тем свойством, что
, обладает тем свойством, что 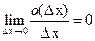 , т. е.
, т. е. 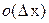 является функцией, бесконечно малой по сравнению с
является функцией, бесконечно малой по сравнению с 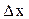 . Функция одной переменной дифференцируема в точке тогда и только тогда, когда имеет производную в этой точке. При этом константа
. Функция одной переменной дифференцируема в точке тогда и только тогда, когда имеет производную в этой точке. При этом константа 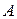 и равна этой производной, т. е. для дифференциала справедлива формула
и равна этой производной, т. е. для дифференциала справедлива формула 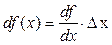 .
.
Если рассматривается частное приращение ФНП 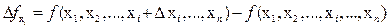 , то меняется только один из аргументов, и это частное приращение можно рассматривать как приращение функции одной переменной, т. е. работает та же теория. Следовательно, условие дифференцируемости
, то меняется только один из аргументов, и это частное приращение можно рассматривать как приращение функции одной переменной, т. е. работает та же теория. Следовательно, условие дифференцируемости 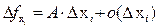 выполнено тогда и только тогда, когда существует частная производная
выполнено тогда и только тогда, когда существует частная производная 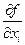 , и в этом случае частный дифференциал определяется формулой
, и в этом случае частный дифференциал определяется формулой 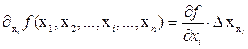 .
.
А что же такое дифференциал ФНП?
Определение 3. Функция 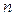 переменных
переменных 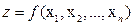 называется дифференцируемой в точке
называется дифференцируемой в точке 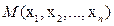 , если ее приращение
, если ее приращение 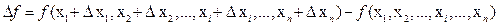 представляется в виде
представляется в виде 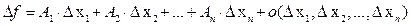 . При этом главная часть приращения называется дифференциалом ФНП.
. При этом главная часть приращения называется дифференциалом ФНП.
Итак, дифференциалом ФНП является величина 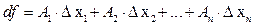 . Уточним, что мы понимаем под величиной
. Уточним, что мы понимаем под величиной 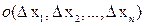 , которую мы будем называть бесконечно малой по сравнению с приращениями аргументов
, которую мы будем называть бесконечно малой по сравнению с приращениями аргументов 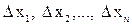 . Это функция, которая обладает тем свойством, что если все приращения, кроме одного
. Это функция, которая обладает тем свойством, что если все приращения, кроме одного 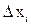 , равны 0, то справедливо равенство
, равны 0, то справедливо равенство 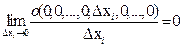 . По сути это означает, что
. По сути это означает, что 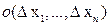 = =
= = 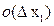 +
+ 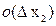 +…+
+…+ 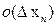 .
.
А как связаны между собой условие дифференцируемости ФНП и условия существования частных производных этой функции?
Теорема 1. Если функция 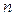 переменных
переменных 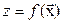 дифференцируема в точке
дифференцируема в точке 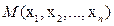 , то у нее существуют частные производные по всем переменным в этой точке и при этом
, то у нее существуют частные производные по всем переменным в этой точке и при этом 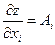 .
.
Доказательство. Равенство 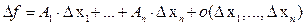 запишем при
запишем при 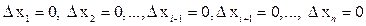 и
и 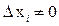 в виде
в виде 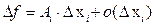 и раздели обе части полученного равенства на
и раздели обе части полученного равенства на 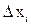 . В полученном равенстве
. В полученном равенстве 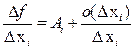 перейдем к пределу при
перейдем к пределу при 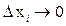 . В итоге мы и получим требуемой равенство
. В итоге мы и получим требуемой равенство 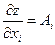 . Теорема доказана.
. Теорема доказана.
Следствие. Дифференциал функции 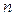 переменных
переменных 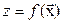 вычисляется по формуле
вычисляется по формуле 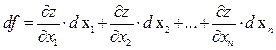 .
.
В примере 1 дифференциал функции 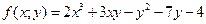 был равен
был равен 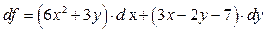 . Заметим, что этот же дифференциал в точке
. Заметим, что этот же дифференциал в точке 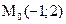 равен
равен 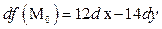 . А вот если мы его вычислим в точке
. А вот если мы его вычислим в точке 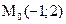 с приращениями
с приращениями 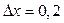 ,
, 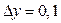 , то дифференциал будет равен
, то дифференциал будет равен 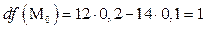 . Заметим, что
. Заметим, что 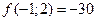 , точное значение заданной функции в точке
, точное значение заданной функции в точке 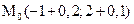 равно
равно 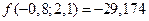 , а вот это же значение, приближенно вычисленное с помощью 1-го дифференциала, равно
, а вот это же значение, приближенно вычисленное с помощью 1-го дифференциала, равно 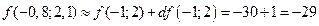
А будет ли функция нескольких переменных дифференцируема в точке, если она имеет частные производные в этой точке. В отличии от функции одной переменной ответ на этот вопрос отрицательный. Точную формулировку взаимосвязи дает следующая теорема.
Теорема 2. Если у функции 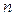 переменных
переменных 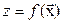 в точке
в точке 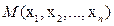 существуют непрерывные частные производные по всем переменным, то функция
существуют непрерывные частные производные по всем переменным, то функция 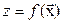 дифференцируема в этой точке.
дифференцируема в этой точке.
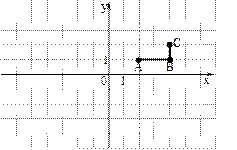
Доказательство. Для наглядности рассмотрим функцию двух переменных 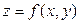 и точки и точки 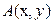 , , 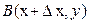 , , 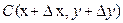 . Полное приращение функции в точке . Полное приращение функции в точке 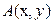 представим в виде представим в виде 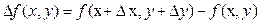 и запишем и запишем
| 
|
в виде 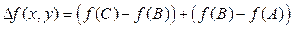 . В каждой скобке меняется только одна переменная, поэтому мы можем и там и там применить формулу конечных приращений Лагранжа. Суть этой формулы в том, что для непрерывно дифференцируемой функции одной переменной разность значений функции в двух точках равна значению производной в некоторой промежуточной точке, умноженному на расстояние между точками. Применяя эту формулу к каждой из скобок, получим
. В каждой скобке меняется только одна переменная, поэтому мы можем и там и там применить формулу конечных приращений Лагранжа. Суть этой формулы в том, что для непрерывно дифференцируемой функции одной переменной разность значений функции в двух точках равна значению производной в некоторой промежуточной точке, умноженному на расстояние между точками. Применяя эту формулу к каждой из скобок, получим 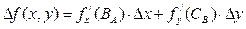 . В силу непрерывности частных производных производная
. В силу непрерывности частных производных производная 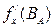 в точке
в точке 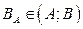 и производная
и производная 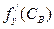 в точке
в точке 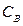 отличаются от производных
отличаются от производных 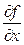 и
и 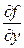 в точке
в точке 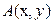 на величины
на величины 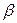 и
и 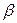 , стремящиеся к 0 при
, стремящиеся к 0 при 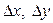 , стремящихся к 0. Но тогда
, стремящихся к 0. Но тогда 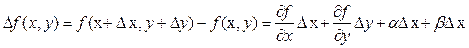 и, очевидно,
и, очевидно, 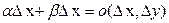 . Теорема доказана.
. Теорема доказана.
| <== предыдущая лекция | | | следующая лекция ==> |
| | | ОСНОВЫ ТЕОРИИ ПРОГНОЗИРОВАНИЯ |
Дата добавления: 2016-02-27; просмотров: 3887;
