Производная давления.
Использование производной давления вместе с типовыми кривыми на одном графике позволяет устранить недостаток типовых кривых, связанный с логарифмическим представлением данных. Это происходит благодаря тому, что производная – более чувстительный инструмент.
Использование производной стало возможным с изобретением высокоточных манометров в середине 80-х годов.
В нефтяной литературе были предложены различные формы производной. В 1983 году Бурде предложил использование логарифмической производной давления:
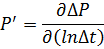
Таким образом, 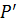 - скорость изменения давления по отношению к логарифму времени, а значит равна тангенсу угла наклона кривой
- скорость изменения давления по отношению к логарифму времени, а значит равна тангенсу угла наклона кривой  на полулогарифмическом графике.
на полулогарифмическом графике.
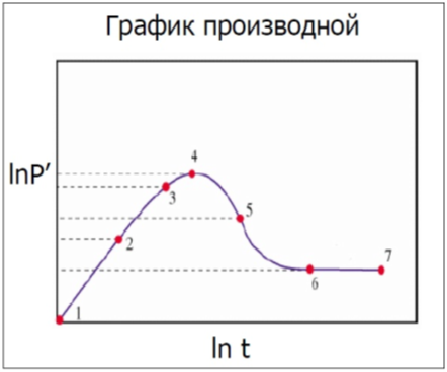
Основная идея производной – вычислить наклон в каждой точке кривой давления на полулогарифмическом графике и нанести точки на график в билогарифмических координатах (рисунок 1 и 2).
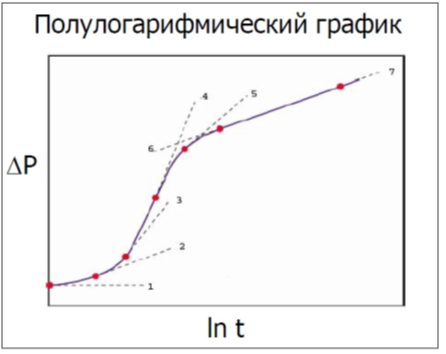
Обычно кривая производной давления представляется на билогарифмическом графике вместе с кривой давления.
Для возможности диагностирования режимов потока на билогарифмическом графике, производную находят для безразмерных параметров 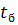 и
и 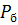 .
.
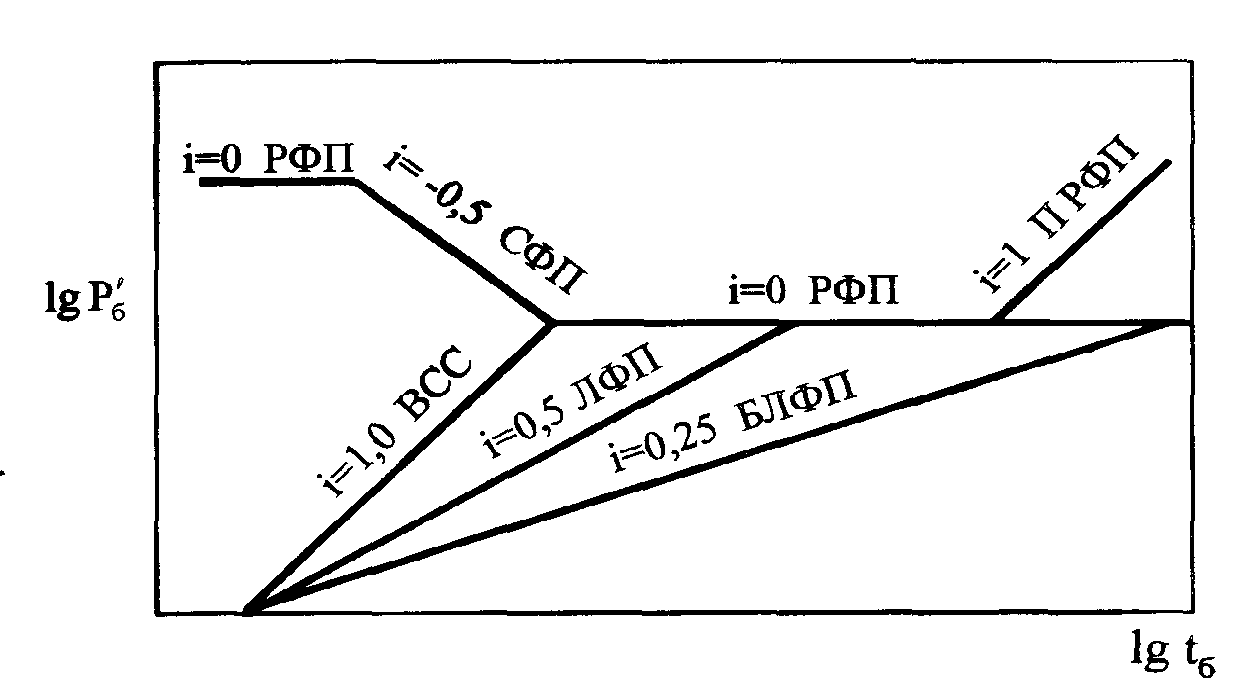
Если в билогарифмических диагностических координатах 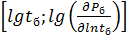 нанести соответствующие кривые простейших одномерных фильтрационных потоков по специальным зависимостям, то все эти графики представятся характерными прямолинейными графиками (рисунок 3) с соответствующими клонами.
нанести соответствующие кривые простейших одномерных фильтрационных потоков по специальным зависимостям, то все эти графики представятся характерными прямолинейными графиками (рисунок 3) с соответствующими клонами.
Процесс дифференцирования может дать очень зашумленную производную, поэтому необходимо сглаживать данные. Существует множество алгоритмов сглаживания данных. В основе этих алгоритмов лежит понятие интервала дифференцирования 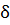 .
.
Для того, чтобы найти значение производной в точке 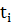 , рассматривают интервал
, рассматривают интервал 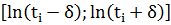 .
.
К наиболее распространенным алгоритмам сглаживания относятся:
1. Многоточечная регрессия.
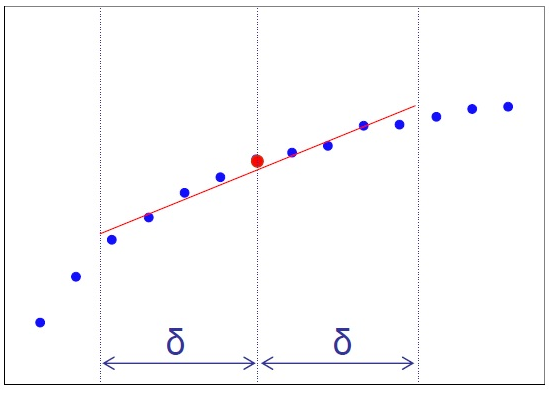
Через точки, попавшие в интервал 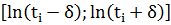 , проводится регрессионная прямая. Наклон этой прямой линии есть значение производной в точке
, проводится регрессионная прямая. Наклон этой прямой линии есть значение производной в точке 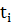 .
.
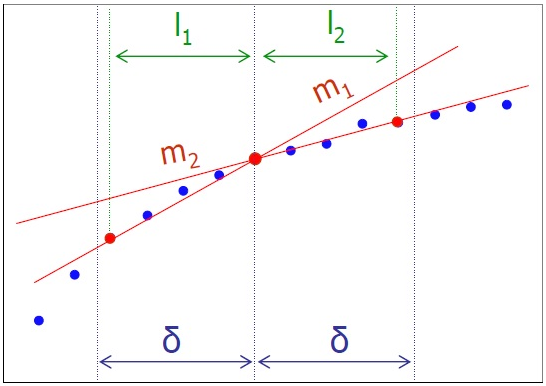
2. Скользящее окошко.
Через точки 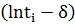 и
и 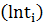 проводят прямую линию, определяют ее наклон
проводят прямую линию, определяют ее наклон 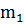 . Через точки
. Через точки 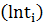 и
и 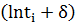 проводят прямую линию, определяют ее наклон
проводят прямую линию, определяют ее наклон 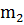 . Производная в точке
. Производная в точке 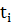 есть среднее арифметическое наклонов
есть среднее арифметическое наклонов 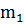 и
и 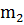 . В общем случае, если точки расположены неравномерно по времени, прямые строятся через точку
. В общем случае, если точки расположены неравномерно по времени, прямые строятся через точку 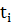 и самые дальние от нее точки, попадающие в интервал
и самые дальние от нее точки, попадающие в интервал 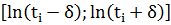 . В данном случае производная равна средневзвешенному наклонов
. В данном случае производная равна средневзвешенному наклонов 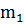 и
и 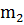 .
.
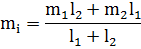
Тема №2. Прямой анализ с помощью производной.
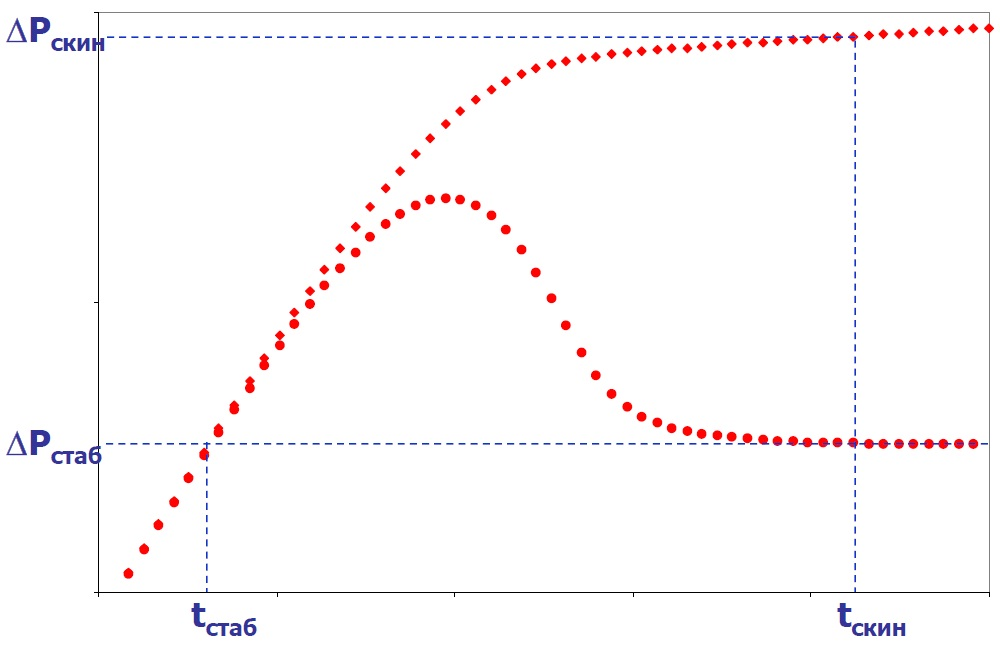
С момента достижения радиального притока производная давления стабилизируется, а безразмерное значение давления равно 0,5. Отсюда:
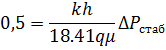
Во время периода ВСС давление линейно зависит от времени:
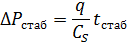
Значение скин-фактора можно найти из соотношения:
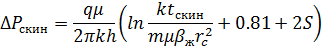
| <== предыдущая лекция | | | следующая лекция ==> |
| Внутренняя энергия, работа и теплота в термодинамике. | | | РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ |
Дата добавления: 2016-04-19; просмотров: 5987;
