Частная производная, полный дифференциал ФНП. Связь дифференцируемости функции с существованием частных производных

Для функции одной вещественной переменной после изучения тем «Пределы» и «Непрерывность» (Введение в математический анализ) изучались производные и дифференциалы функции. Перейдем к рассмотрению аналогичных вопросов для функции нескольких переменных. Заметим, что если в ФНП зафиксировать все аргументы, кроме одного, то ФНП порождает функцию одного аргумента, для которой можно рассматривать приращение, дифференциал и производную. Их мы будем называть соответственно частное приращение, частный дифференциал и частная производная. Сумма частных приращений и частных дифференциалов по всем переменным (аргументов ФНП) будут соответственно называться полными приращениями и полными дифференциалами. Что касается производной, то понятия полной производной для ФНП нет.

Определение 1. Система векторов 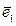, ,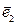…, 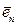называется линейно независимой системой векторов, если из равенства 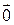ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.

Ввв