Дифференцирование сложной функции многих переменных.

Частные и полные приращения функции двух и нескольких переменных.

Множество элементов произвольной природы называется векторным пространством или линейным векторным пространством, если для этих элементов введены операции сложения и умножения на действительное число, причем для этих операций справедливы 8 свойств, указанных для операций с геометрическими векторами.

определим скалярное произведение этих векторов формулой . Несложно проверить, что все свойства скалярного

Определение 2. Система векторов 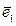, ,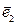…, 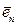называется линейно независимой системой векторов, если из равенства 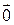ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.

Определение 3. Линейно независимая система векторов линейного векторного пространства 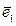, ,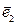…, 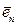называется базисом этого векторного пространства, если каждый его вектор является линейной комбинацией векторов 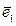, ,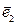…, 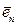. При этом коэффициенты этой линейной комбинации определяются однозначно и называются координатами вектора в этом базисе.