Функции многих переменных. Предел и непрерывность ФМП
Под функцией мы понимаем отображение одного множества на другое. До сих пор мы рассматривали функцию вида 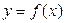 , которая реализовывала отображение множества на оси абсцисс (область определения функции) на множество на оси ординат (множество значений функции
, которая реализовывала отображение множества на оси абсцисс (область определения функции) на множество на оси ординат (множество значений функции 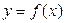 ).
).
Под функцией нескольких переменных мы будем понимать отображение множества в 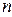 -мерном евклидовом пространстве
-мерном евклидовом пространстве  (область определения функции) на множество на оси (множество значений функции). Тем самым функция нескольких переменных может быть записана в виде
(область определения функции) на множество на оси (множество значений функции). Тем самым функция нескольких переменных может быть записана в виде 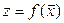 , где
, где  - элемент евклидова пространства. Можно использовать запись
- элемент евклидова пространства. Можно использовать запись 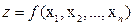 .
.
Изучая функцию одной переменной 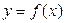 , мы изучали числовые последовательности, предел числовой последовательности, предел функции, непрерывность функции, точки экстремума функции.
, мы изучали числовые последовательности, предел числовой последовательности, предел функции, непрерывность функции, точки экстремума функции.
Наша цель – построить и изучить аналогичную теорию для ФМП. Этот раздел посвящен вопросам, связанным с пределами и непрерывностью функций.
Давайте вспомним, что такое предел функции одной переменной. Предел функции 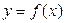 (по Коши) при
(по Коши) при  , стремящимся к
, стремящимся к 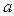 , равен
, равен  , если для каждого, сколь угодно малого положительного числа
, если для каждого, сколь угодно малого положительного числа 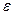 найдется положительное число
найдется положительное число 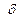 , обладающее следующим свойством. Если расстояние от точки
, обладающее следующим свойством. Если расстояние от точки  до не равной ей точки
до не равной ей точки 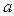 меньше
меньше 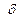 , то модуль разности чисел
, то модуль разности чисел  и
и  меньше наперед заданного числа
меньше наперед заданного числа 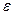 (
( 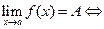
 ).
).
Для того, чтобы дать это и аналогичные определения для ФМП, надо ввести расстояние между точками – аргументами ФНП (=ФМП). Это делают следующим образом. Пусть начало координат с ортонормированным базисом находится в точке  и заданы две точки
и заданы две точки  и
и 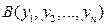 . Рассмотрим векторы
. Рассмотрим векторы  ,
,  и определим скалярное произведение этих векторов формулой
и определим скалярное произведение этих векторов формулой  . Несложно проверить, что все свойства скалярного произведения выполнены. Именно так и принято вводить скалярное произведение в евклидовом пространстве.
. Несложно проверить, что все свойства скалярного произведения выполнены. Именно так и принято вводить скалярное произведение в евклидовом пространстве.
При наличии скалярного произведения, которое гарантированно есть в евклидовом пространстве, можно ввести длину вектора и расстояние между точками евклидова пространства, что позволяет обобщить понятия предела последовательности, предела функции, непрерывности функции на случай ФНП.
Длиной вектора 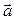 мы назовем квадратный корень из его скалярного квадрата, т. е.
мы назовем квадратный корень из его скалярного квадрата, т. е. 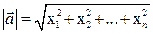 . Расстоянием между точками
. Расстоянием между точками  и
и 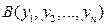 равно длине вектора
равно длине вектора 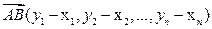 , их соединяющего, т. е.
, их соединяющего, т. е. 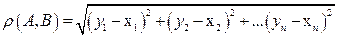 .
.
Заметим, что это определение обобщает обычное расстояние между точками на плоскости и в пространстве, известные нам из школы.
Пример 1. Расстояние между точками 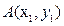 и
и 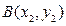 на плоскости равно длине вектора
на плоскости равно длине вектора  , их соединяющего, т. е.
, их соединяющего, т. е. 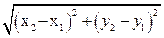 . Расстояние между точками
. Расстояние между точками 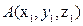 и
и 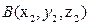 в пространстве равно длине вектора
в пространстве равно длине вектора 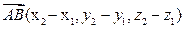 , их соединяющего, т. е.
, их соединяющего, т. е. 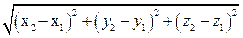 .
.
Сформулируем определение предела для последовательности точек в евклидовом пространстве.
Определение 1. Пусть задана последовательность точек 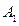 ,
, 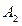 ,…,
,…, 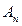 ,…. Мы будем говорить, что число
,…. Мы будем говорить, что число  является пределом этой последовательности, т. е.
является пределом этой последовательности, т. е. 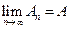 , если для каждого, сколь угодно малого положительного числа
, если для каждого, сколь угодно малого положительного числа 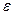 найдется номер
найдется номер 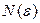 , зависящий от
, зависящий от 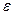 , такой что при выполнении условия
, такой что при выполнении условия  выполнено условие
выполнено условие 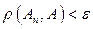 . (
. ( 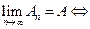
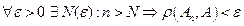 ).
).
Пример 2. Заметим, что условию  удовлетворяют точки
удовлетворяют точки 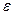 -окрестности точки
-окрестности точки 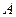 . В одномерном случае для функции одной переменной окрестностью точки на оси является интервал длины
. В одномерном случае для функции одной переменной окрестностью точки на оси является интервал длины 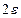 . Для плоскости – пространства размерности 2 такой
. Для плоскости – пространства размерности 2 такой 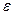 -окрестностью является внутренность круга радиуса
-окрестностью является внутренность круга радиуса 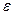 . Для реально пространства – пространства размерности 3 такой
. Для реально пространства – пространства размерности 3 такой 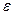 -окрестностью является внутренность шара радиуса
-окрестностью является внутренность шара радиуса 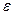 .
.
Сформулируем определение предела для ФНП.
Определение 2. Пусть задана функция 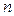 переменных
переменных 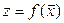 где
где  - элемент евклидова пространства. Мы будем говорить, что число
- элемент евклидова пространства. Мы будем говорить, что число  является пределом этой функции, т. е.
является пределом этой функции, т. е. 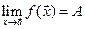 , если для каждого, сколь угодно малого положительного числа
, если для каждого, сколь угодно малого положительного числа 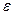 найдется положительное число
найдется положительное число 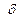 , обладающее следующим свойством. Если расстояние от точки
, обладающее следующим свойством. Если расстояние от точки 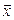 до не равной ей точки
до не равной ей точки 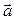 меньше
меньше 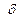 , то модуль разности чисел
, то модуль разности чисел 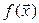 и
и  меньше
меньше 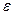 . Формально это записывается в виде:
. Формально это записывается в виде: 
 .
.
Это определение соответствует определению предела функции одной переменной по Коши, которое эквивалентно определению предела функции по Гейне. Формулировка определения предела функции по Гейне, которая сохраняется для функции нескольких переменных, заключается в записи 
 . Смысл этого в том, что
. Смысл этого в том, что 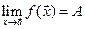 означает с учетом области определения, что из того, что предел последовательности аргументов равен
означает с учетом области определения, что из того, что предел последовательности аргументов равен 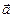 , следует, что предел соответствующих значений функции равен
, следует, что предел соответствующих значений функции равен 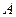 .
.
Перейдем к определению непрерывности ФНП. Здесь полностью сохраняются формулировки определения непрерывности для функции одной переменной. Функция непрерывна в точке, если предел функции при подходе к этой точке равен значению функции в этой точке. Запишем это формально.
Определение 3. Пусть задана функция 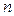 переменных
переменных 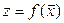 где
где  - элемент евклидова пространства. Мы будем говорить, что функция
- элемент евклидова пространства. Мы будем говорить, что функция 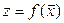 непрерывна в точке
непрерывна в точке 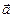 , если
, если 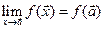 .
.
Соответственно функция непрерывна на множестве, если она непрерывна в каждой точке этого множества.
Пример 3. Найдите пределы функций: а) 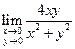 , б)
, б) 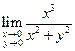 и исследуйте функции в)
и исследуйте функции в) 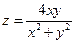 , г)
, г) 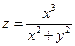 на непрерывность.
на непрерывность.
Докажем, что 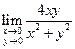 не существует. В самом деле, пусть мы приближаемся к предельной точке
не существует. В самом деле, пусть мы приближаемся к предельной точке 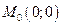 по прямой
по прямой 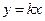 . На этой прямой значение функции
. На этой прямой значение функции 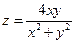 равно
равно 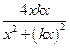 , т. е. во всех точках, кроме предельной, равно
, т. е. во всех точках, кроме предельной, равно  . Эта величина зависит от
. Эта величина зависит от 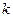 , следовательно,
, следовательно, 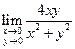 не существует.
не существует.
Дата добавления: 2016-02-20; просмотров: 2453;
