Евклидово пространство
Вспомним некоторые важные понятия, изученные в 1 семестре. Мы познакомились с векторами на плоскости и в пространстве. Векторы на плоскости обладают рядом важных свойств. Для них введены операции сложения векторов и умножения вектора на число. Результатом этих операций являются вектора на плоскости, причем справедливы следующие 8 свойств: 1) 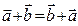 - коммутативность, 2)
- коммутативность, 2) 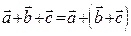 - ассоциативность, 3)
- ассоциативность, 3) 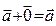 - существование нулевого элемента, 4)
- существование нулевого элемента, 4)  существование противоположного элемента
существование противоположного элемента 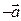 , 5)
, 5)  ,
,
6) 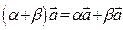 дистрибутивность для числовых коэффициентов,
дистрибутивность для числовых коэффициентов,
7) 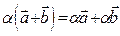 - дистрибутивность для векторов, 8)
- дистрибутивность для векторов, 8) 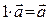 .
.
Определение 1. Множество элементов произвольной природы называется векторным пространством или линейным векторным пространством, если для этих элементов введены операции сложения и умножения на действительное число, причем для этих операций справедливы 8 свойств, указанных для операций с геометрическими векторами.
Пусть заданы векторы 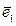 ,
, 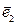 ,…,
,…, 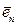 векторного пространства и числа
векторного пространства и числа 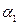 ,
,  ,…,
,…, 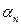 . Величина
. Величина  (1)
(1)
называется линейной комбинацией заданных векторов 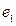 ,
, 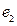 ,…,
,…,  . При этом числа
. При этом числа 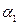 ,
,  ,…,
,…, 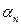 называются коэффициентами линейной комбинации (1). Очевидно, что линейная комбинация векторов равна
называются коэффициентами линейной комбинации (1). Очевидно, что линейная комбинация векторов равна 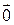 (нулевому вектору), если все коэффициенты линейной комбинации равны 0.
(нулевому вектору), если все коэффициенты линейной комбинации равны 0.
Определение 2. Система векторов 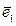 ,
, 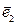 ,…,
,…, 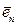 называется линейно независимой системой векторов, если из равенства
называется линейно независимой системой векторов, если из равенства 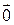 ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.
ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.
Определение 3. Линейно независимая система векторов линейного векторного пространства 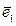 ,
, 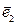 ,…,
,…, 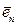 называется базисом этого векторного пространства, если каждый его вектор является линейной комбинацией векторов
называется базисом этого векторного пространства, если каждый его вектор является линейной комбинацией векторов 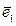 ,
, 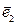 ,…,
,…, 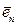 . При этом коэффициенты этой линейной комбинации определяются однозначно и называются координатами вектора в этом базисе.
. При этом коэффициенты этой линейной комбинации определяются однозначно и называются координатами вектора в этом базисе.
Мы знаем, что для геометрических векторов справедливы следующие свойства скалярного произведения:
1) 
2) 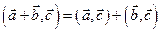
3) 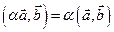
4) 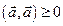 ,
,  .
.
Определение 4. Пусть в линейном векторном пространстве введена операция, ставящая в соответствие двум векторам число. Такое соответствие, удовлетворяющее условиям 1) – 4) называется скалярным произведением векторов и обозначается символом  или
или 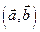 .
.
Определение 5. Линейное векторное пространство 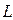 с введенным скалярным произведением называется евклидовым пространством
с введенным скалярным произведением называется евклидовым пространством 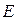 .
.
Можно доказать, что элементов базиса линейного векторного пространства не зависит от выбора базиса. Это число и называется размерностью такого пространства. Линейное пространство может быть бесконечно мерным.
Отметим, что 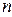 -мерные векторные и евклидовы пространства обозначаются соответственно символами
-мерные векторные и евклидовы пространства обозначаются соответственно символами 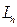 и
и  .
.
Мы знаем, что наиболее удобными базисами на плоскости и в пространстве являются системы взаимно перпендикулярных векторов единичной длины. Евклидовы пространства замечательны тем, что при наличии произвольного базиса из 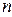 векторов можно с помощью разрешенных линейных операций создать ортонормированный базис.
векторов можно с помощью разрешенных линейных операций создать ортонормированный базис.
Определение 6. Базис в евклидовом линейного векторного пространства 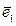 ,
, 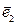 ,…,
,…, 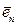 называется ортонормированным базисом, если
называется ортонормированным базисом, если 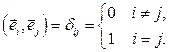
Дата добавления: 2016-02-20; просмотров: 571;
