Поняття про критерії подібності. Кількість лінійно незалежних критеріїв подібності
В теорії подібності велике значення мають безрозмірні комплекси величин, які є добутком різних степенів цих величин. Їх називають критеріями подібності і позначають 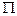 . Критерії подібності використовуються як параметри, так і змінні досліджуваної системи. Скільки незалежних між собою критеріїв можна утворити з
. Критерії подібності використовуються як параметри, так і змінні досліджуваної системи. Скільки незалежних між собою критеріїв можна утворити з 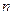 розмірних величин? Незалежність
розмірних величин? Незалежність 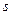 величин
величин 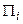 означає, що
означає, що
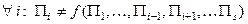 .
.
Будемо розглядати електромеханічні системи з їх основними одиницями 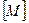 ,
, 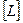 ,
, 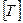 ,
, 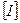 . Нехай задано
. Нехай задано 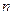 величин
величин 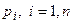 . Тоді
. Тоді
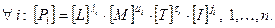
Будь-який критерій подібності – це деяка комбінація величин 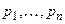 :
:
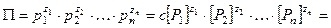
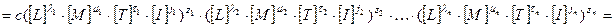
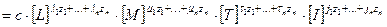 .
.
Оскільки критерії подібності – величини нульової розмірності, то всі степені повинні бути рівні нулю, тобто:
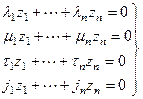 . (3.1)
. (3.1)
Таким чином, отримано систему з 4-х рівнянь, які містять 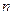 невідомих
невідомих 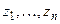 . Як відомо, така система має
. Як відомо, така система має 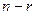 лінійно незалежних розв’язків, де
лінійно незалежних розв’язків, де 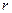 - ранг матриці системи (5.1). Кожний розв'язок дає змогу отримати один критерій подібності
- ранг матриці системи (5.1). Кожний розв'язок дає змогу отримати один критерій подібності
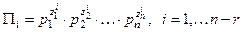 . (3.2)
. (3.2)
Ці 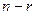 незалежних критеріїв називають фундаментальними. Будь-який інший розв’язок системи (3.1) буде лінійно залежним та буде породжувати відповідний критерій подібності, який також буде залежним від фундаментальних критеріїв (3.2).
незалежних критеріїв називають фундаментальними. Будь-який інший розв’язок системи (3.1) буде лінійно залежним та буде породжувати відповідний критерій подібності, який також буде залежним від фундаментальних критеріїв (3.2).
Отже, з заданих 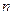 величин можна побудувати
величин можна побудувати 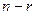 незалежних критеріїв подібності, де
незалежних критеріїв подібності, де 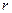 - ранг матриці системи (3.1). Причому ранг матриці не може бути більшим від кількості основних одиниць. Загальне правило визначення рангу
- ранг матриці системи (3.1). Причому ранг матриці не може бути більшим від кількості основних одиниць. Загальне правило визначення рангу 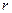 можна сформулювати так: якщо серед заданих
можна сформулювати так: якщо серед заданих 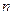 величин вибрано
величин вибрано 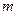 первинних з незалежними розмірностями, то
первинних з незалежними розмірностями, то 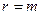 , у протилежному випадку
, у протилежному випадку 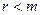 . Кількість незалежних критеріїв подібності можна зменшити шляхом збільшення числа основних одиниць вимірювання, але лише при умові, розмірний коефіцієнт, що з’являється при цьому, не входить в рівняння, що описують систему.
. Кількість незалежних критеріїв подібності можна зменшити шляхом збільшення числа основних одиниць вимірювання, але лише при умові, розмірний коефіцієнт, що з’являється при цьому, не входить в рівняння, що описують систему.
Поняття подібності
Конкретизуємо зміст понять, які розглядалися раніше в широкому змісті. Під системою будемо розуміти сукупність фізичних об’єктів (елементів системи), об’єднаних на основі деякої ознаки, що надає системі певні властивості. Будемо мати на увазі такі системи, стан яких є однозначною функцією станів окремих її елементів. Параметрами системи називатимемо величини, які характеризують її елементи і впливаючі на систему зовнішні фактори. Параметри дають змогу індивідуалізувати конкретний об’єкт з множини інших об’єктів тієї ж фізичної природи. Узагальненими координатами системи називають величини, які описують поведінку системи. Їх кількість рівна числу ступенів свободи системи.
З множини параметрів виділяємо мінімально можливу кількість параметрів, яких достатньо для однозначного визначення стану системи. Ці параметри є незалежними між собою і називаються основними (визначальними). Розглянемо дві системи однакової фізичної природи, які складаються з однакової кількості елементів, причому відповідні елементи в цих системах відіграють однакову роль. Одну систему назвемо модель, а іншу – оригінал. Кожна система визначається 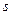 основними параметрами
основними параметрами 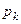 та має
та має 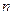 незалежних узагальнених координат
незалежних узагальнених координат 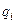 . Узагальнені координати цих систем мають однакову функціональну залежність від параметрів:
. Узагальнені координати цих систем мають однакову функціональну залежність від параметрів:
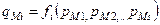 ,
, 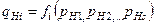 .
.
Дві системи називаються подібними, якщо будь-які дві відповідні узагальнені координати для будь-яких схожих моментів часу пропорційні, тобто:
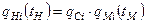 ,
,
де 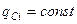 - коефіцієнт подібності,
- коефіцієнт подібності, 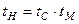 ,
, 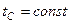 ,
, 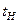 ,
, 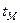 - схожі моменти часу.
- схожі моменти часу.
Таким чином, якщо відомо, що дві системи подібні і можна знайти коефіцієнти подібності 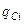 , то знаючи поведінку однієї системи (моделі), можна визначити, як буде вести себе інша (натура).
, то знаючи поведінку однієї системи (моделі), можна визначити, як буде вести себе інша (натура).
Розглянемо ряд прикладів застосування теорії подібності. Зокрема, якщо для двох механічних систем, виконуються рівності: 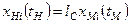 ,
, 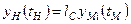 ,
, 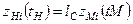 , то такі системи будуть кінематично подібні. Окрім того, якщо між точками систем має місце ще й матеріальна подібність, тобто
, то такі системи будуть кінематично подібні. Окрім того, якщо між точками систем має місце ще й матеріальна подібність, тобто 
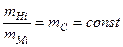 , то такі системи будуть динамічно подібними. У цьому випадку, дуже легко встановити зв’язок між усіма кінематичними та динамічними характеристиками систем. Так, для швидкості:
, то такі системи будуть динамічно подібними. У цьому випадку, дуже легко встановити зв’язок між усіма кінематичними та динамічними характеристиками систем. Так, для швидкості:
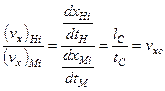 ,
, 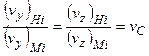 ,
,
для прискорень: 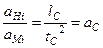 ,
,
для сили: 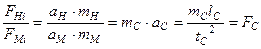 ,
,
для роботи: 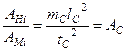 ,
,
для потужності: 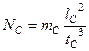 .
.
При наявності динамічної подібності коефіцієнти подібності різних величин виражаються через вихідні коефіцієнти подібності 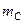 ,
, 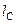 ,
, 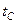 за допомогою формул розмірності цих величин.
за допомогою формул розмірності цих величин.
Досить часто коефіцієнти подібності одних вторинних величин зручно виражати через коефіцієнти подібності інших вторинних величин. Так, наприклад,
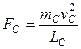 .
.
Якщо густина відповідних частин обох систем однакова, тобто 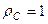 , то
, то 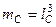 і
і 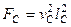 . Якщо системи – дві динамічно подібні машини однакових розмірів (або одна і та ж машина в різних режимах роботи), тобто
. Якщо системи – дві динамічно подібні машини однакових розмірів (або одна і та ж машина в різних режимах роботи), тобто 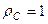 ,
, 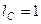 , то
, то 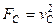 , тобто прикладені до певних точок машини сили співвідносяться як квадрати швидкостей цих точок машини. Відношення потужностей у цьому випадку
, тобто прикладені до певних точок машини сили співвідносяться як квадрати швидкостей цих точок машини. Відношення потужностей у цьому випадку 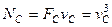 , тобто, якщо швидкість машини збільшиться вдвічі, то сили збільшаться у 4 рази, а потужність – у 8 разів.
, тобто, якщо швидкість машини збільшиться вдвічі, то сили збільшаться у 4 рази, а потужність – у 8 разів.
Дата добавления: 2016-04-22; просмотров: 1612;
