Упражнение I. Измерение линейной дисперсии и разрешающей способности спектрографа.

Основными характеристиками спектральных аппаратов являются дисперсия и разрешающая сила. Линейная дисперсия 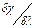показывает, сколько миллиметров длины спектра в данном месте его приходится на один ангстрем. Разрешающей силой, либо способностью, спектрального аппарата называется отношение наблюдаемой длины волны λ к той наименьшей разности δλ двух длин волн, которые ещё могут быть разрешены с помощью данного аппарата.

Для определения дисперсии и разрешающей способности спектрогра­фа необходимо сфотографировать известный спектр. В качестве такого в данном случае используют спектр ртути, длины волн линий которого хорошо известны. Для фотографирования ртутная лампа устанавливается перед входной щелью спектрографа, ширина которой выбирается в преде­лах 0,005 -.0,001 мм. Для получения подходящего по почернению снимка спектр фотографируют с несколькими выдержками. После фотографирования спектра ртути снимают спектр вещества, неизвестные длины волн которого необходимо определить (в упражнении 2).Условия фотографирования указываются руководителем.

Полученный снимок спектра ртути используют для определения линейной дисперсии и разрешающей способности спектрографа. Для этого с помощью измерительного микроскопа измеряют расстояния спектральных линий, длины волн которых найдены сравнением с эталонным спектром, от какой-либо линии, расположенной на одном из краёв спектра, т.е. определяют координаты х спектральных линий на фотопластинке.

Измерив относительное положение линий, строят дисперсионную кривую x(λ), откладывая по оси абсцисс длины волн в ангстремах, а по оси ординат соответствующие значения х. Выбирают точек пять, равномерно расположенных вдоль дисперсионной кривой, и в окрестности каж­дой из них определяют линейную дисперсию призмы δх/δλ как тангенс угла наклона касательной к кривой в данной точке. (Одна из точек должна быть выбрана в районе λ=2570 Å.

Далее для длины волны 2573 Å, для которой призма установлена под углом наименьшего отклонения, определяют разрешающую способность призмы по формуле

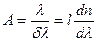(1)

Длина основания призмы l = 47 мм. Следовательно, для определения раз­решающей способности призмы нужно знать только её дисперсию dn/dλ. Дисперсию материала призмы можно найти через ранее определённую линейную дисперсию δх/δλ. Действительно, при угле наименьшего отклонения φ показатель преломления n может быть определён из выражения

(2)

где α- преломляющий угол призмы. Откуда

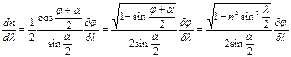(3)

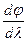- угловая дисперсия, связанная с линейной дисперсией соот­ношением 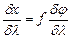(4)

а f - фокусное расстояние камерного объектива (f=831 мм для l=2573 Å). Определив из рис. 1 значение угла наименьшего отклонения, вычисляют значение показателя преломления n. Подставив полученное значение n и определённое из (4) значение δφ/δλ в (3), находят dn/dλ, a затем по (1) и разрешающую способность призмы.