Основные определения. Общая задача линейного программирования

Общая задача линейного программирования

Дана система m линейных уравнений и неравенств с n переменными

,

………………………….

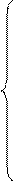
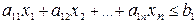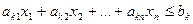, (1.1)

,

,

…………………………..,

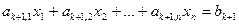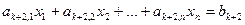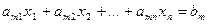
где .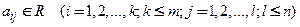

И линейная функция

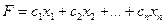, (1.2)

где .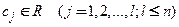

Необходимо найти такое решение системы Х=(х₁, х₂, …, х_n), где

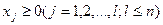(1.3)

при котором линейная функция F (1.1) принимает оптимальное значение.

Система (1.1) называется системой ограничений, а функция F – линейной функцией.

Оптимальным решением задачи линейного программирования называется решение Х=(х₁, х₂, …, х_n) системы ограничений (1.1), удовлетворяющее условию (1.3), при котором линейная функция (1.2) принимает оптимальное значение.

Основные определения

Любые m переменных системы m линейных уравнений с n переменными (m<n) называются основными или базисными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные n-m переменных называются неосновными.

Теорема 1.1. Если для системы m линейных уравнений с n переменными (m<n) ранг матрицы коэффициентов при переменных равен m, т.е. существует хотя бы одна группа основных переменных, то эта система является неопределенной, причем каждому произвольному набору значений неосновных переменных соответствует одно решение системы.

Базисным решением системы m линейных уравнений с n переменными называется решение, в котором все n-m неосновных переменных равны нулю.

Угловая точка – точка множества, которая не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.

Теорема 1.2. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более, чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой комбинацией этих точек.

Оптимум линейной функции задачи линейного программирования следует искать среди конечного числа ее допустимых базисных решений.