Поняття про мову UML

Мова UML – є мовою семантичного моделювання предметних областей та подальшого проектування відповідних програмних засобів.

В основі мови – виділення класів, опис їх характеристик та взаємозв’язків. У 1997 р. мова була прийнята консорціумом OMG(Object Management Group) як стандарт. Основою опису предметної області є діаграма класів (може бути реалізована в об’єктно-орієнтованих мовах).

Відношення між класами:

1. Асоціація – описує структурні зв’язки між класами.
2. Узагальнення – відношення „Є” (клас / підклас)
3. Залежність – вплив однієї сутності на іншу.

7.4. ЛОГІЧНІ МОДЕЛІ ТА МЕТОД РЕЗОЛЮЦІЙ

7.4.1. Логічні побудови та логічні моделі

Завдання: так формалізувати логічні побудови, щоб вони виконувалися автоматично (комп’ютер). Найкраще піддається автоматизації дедуктивний спосіб виведення.

Розглянемо дві задачі автоматизації дедуктивних побудов:

1) задача виведення наслідків: знайти всі вірно побудовані формули, які можна логічним шляхом вивести з аксіом на основі правил виведення (знайти всі наслідки з фактів);

2) задача перевірки правильності твердження (автоматичного доведення теорем).

Автоматизація дедуктивних побудов – в ЕС.

Механізм автоматичного доведення теорем покладений в основу логічного програмування. Найвідоміший представник логічного програмування – мова Пролог.

Людська логіка – інтелектуальна модель з нечіткою структурою.

Логічна модель – формальна система, що задається <Т, Р, А, В>

, де Т – множина базових елементів (алфавіт)

Р – множина синтаксичних правил

А - множина аксіом (формули, які приймаються за істинні)

В – множина правил виведення

7.4.2. Вступ до числення предикатів

Предикат – логічна функція (вірність або хибність певного твердження – „Х більше 2”).

Логіка предикатів – мат. апарат формалізації людського мислення.

Числення предикатів використовує:

1) константи (константні терми): С₁, С₂, ..

2) змінні (змінні терми): х₁, х₂, ...

3) функціональні літери: f₁, f₂, …

4) предикатні літери: р₁, р₂, ...

5) логічні символи: →, ↔, , &, ~, , .

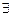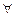Елементарне твердження складається з предиката і зв’язаних з ним термів. Складні твердження будуються з елементарних за допомогою логічних зв’язок: „і” (and, & ), „або” (or, ), „ні” (not, ~), імплікації „→” (якщо ..., тоді ...)

Якщо твердження позначити через a i b, то

Зв’язок	Запис	Інтерпретація
Заперечення	~a	не є a
Кон’юнкція	a&b	a та b
Диз’юнкція	a b	a або b
Імплікація	a→b	a випливає з b
Тотожність (еквівалентність)	a↔b	a еквівалентне b

Імплікація: Чоловік(Х) → Людина(Х)

Для імплікації і тотожності справедливі твердження:

1) a→b дорівнює (~a) b

2) a↔b дорівнює (a&b) (~a & ~b)

3) a↔b дорівнює (a→b) & (b→a)

З кожним предикатом може бути пов’язаний квантор – елемент, який визначає, за яких умов предикат може перетворюватися на істинне висловлювання.

Розрізняють квантор узагальнення ( 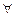) і квантор існування ( ).

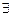Якщо u - змінна, r - твердження, то запис

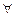“ u r” означає „r справджується для всіх u” (узагальнення, для будь-якого u, all);

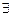“ u r” означає „існує u, для якого r справджується” (існування, існує хоча б одне uдля якого ..., exists);

Приклад: All (Х, чоловік(Х) →людина (Х))

Елементарним об’єктом, який має значення „істина”, є атомарна формула (літерал):

P(t₁, t₂, …, t_n), де Р – предикат, t – терми, n -арність предикату.

Хибна формула: „”.

Тавтології (тотожньо істинні формули): ~~A↔A.

Позитивний літерал не стоїть під знаком заперечення, а негативний – під знаком заперечення.

Диз’юнктом (фразою теорії) називається диз’юнкція деякої кількості атомарних формул.

Часто використовують фрази спеціального типу – фрази Хорна (хорнівські диз’юнкти) – диз’юнкція довільної кількості атомарних формул, з яких позитивною є не більше ніж одна (~A ~B ~C D).

Фрази Хорна по суті є імплікаціями, оскільки за правилами Моргана

(~A ~B ~C D) еквівалентне (A B C ) → D.

Для практичного застосування у логічних виразах потрібно позбутися кванторів узагальнення та існування (пренексна нормальна форма).

Для усунення кванторів існування використовують константи і функції Сколема. Наприклад:

1) Маємо формулу 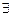x: P(x) вкажемо предметну константу С (константу Сколема), для якої твердження P(C)є істинним; таким чином перейдемо від 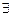x: P(x)до P(C).

2) Маємо формулу 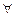y 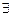x: P(x,y), вкажемо деякий елемент С, для якого твердження P(|C,y)є істинним, тому можна перейти від формули 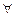y 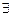x: P(x,y)до формули 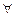y P(h(y), y), де h(y)– функція Сколема.

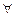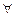Квантори узагальнення просто видаляються (вважається, що якщо фраза залежить від деяких змінних, то всі вони зв’язані оператором узагальнення); формула x y 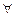z P(x,y,z) замінюється на P(x,y,z).

7.4.3. Фразова форма запису логічних формул

Для спрощення логічних формул використовують рівності

1) ~(а&b) означає (~а) (~b);

2) ~Exists(u,r) означає All(u,~r);

3) ~All(u,r) означає Exists(u,~r).

В результаті перетворень отримуються хорнівські фрази, наприклад (~A ~B ~C D), яка еквівалентна D←(A B C ), а в мовах логічного програмування записується як D:- A, B, C.

7.4.4. Побудова теорії певної області знань

Побудова теорії певної області знань включає дослідження структури цієї області і вибір позначень для її елементів. Потім будується множина вірно побудованих формул (ВПФ) для опису цієї структури. Множина ВПФ є теорією цієї області знань, в якій кожна ВПФ – аксіома.

Для побудови бази знань певної предметної області використовують наступні принципи:

1. Визначаються предметні змінні.
2. База знань описується як кон’юнкція деяких тверджень (фактів або правил виведення).
3. Факти задаються позитивним або негативним літералом, що не містить змінних.
4. Правила виведення задаються фразами Хорна.
5. Квантори існування усуваються шляхом введення констант і функцій Сколема.
6. Квантори узагальнення усуваються механічно.
7. Після побудови формалізованої бази знань здійснюється логічне виведення.

7.4.5. Логічне програмування (+ Пролог)

В логічному програмуванні для автоматичного доведення певного твердження (ВПФ) використовується метод від супротивного: береться інверсія ВПФ і додається до бази знань; якщо при цьому виникає протиріччя (A & ~A) , то ВПФ вважається вірною.

Фрази бази знань можуть бути спрощені методом резолюцій. Для цього знаходиться дві фрази, які утворюють контрарну пару. В контрарній парі одна фраза містить певну атомарну формулу без заперечення, а інша фраза – ту ж формулу із запереченням.

Предметні константи: W- вовк, M - м’ясо. Отримаємо БЗ : G(W,M); ~G(x,M) Q(x) Додамо до БЗ заперечення: G(W,M); ~G(x,M) Q(x) ~Q(W) Резолюція двох останніх записів дає ~G(W,M), тобто виникає протиріччя

M

L

L

Приклад застосування методу резолюцій.

Дано набір фраз:

„вовк їсть м’ясо”

„тварини, які їдять м’ясо, є хижаками”

Потрібно довести, що „вовк є хижаком”

Введемо предикати

G(x,y) => „х їсть у”

Q(x) => „х є хижак”

7.5. Продукційні моделі

7.5.1. Характеристика продукцій них моделей

Продукційною називається модель знань, в якій база знань складається із сукупності продукцій, тобто правил „Якщо А, тоді В”. Термін „продукція” введений американським математиком Е.Постом. Приклади продукцій для зоологічного парку:

„Якщо тварина є птахом, вона не літає, вона плаває, має чорно-білий колір – то це пінгвін”

Такі продукції описують імплікації (з істиності Авипливає істинність В).

Приклад для системи керування технологічним процесом:

„Якщо температура перевищує 200 градусів, то ввімкнути систему охолодження”

Такі продукції задають умовні операції (якщо справедлива умова А, то виконати дію В).

Продукційна система – це база знань разом з механізмом керування продукціями.

Продукційна модель – подання знань у вигляді сукупності продукцій:

(і) Q; P; A B ; N ,

де (і) – ім’я продукції, Q - сфера застосування продукції (предметна область), P - умова застосування продукції, A B ядро продукції, N - постумова продукції.

Приклад: „(БС-29) Банківська сфера; клієнт має рахунок у банку на достатню суму; якщо клієнт бажає зняти певну суму грошей, то він повинен написати ордер; внести зміни до бази даних”.

Продукційні моделі можна поєднувати з семантичними мережами, де знання описуються семантичними мережами, а операції над знаннями задаються як продукції.

Переваги продукцій них моделей:

1. Більшість людських знань можна описати у вигляді продукцій.

2. Більшість продукцій є взаємно незалежними.

3. Продукційні моделі можуть реалізувати будь-які алгоритми.

4. Продукції можуть працювати паралельно.

Основний недолік продукцій – складність перевірки правильності функціонування.

7.5.2. Продукції та мережі виведення

Системи продукцій можна зображати у вигляді графів – мереж виведення.Вершини графу відповідають умовам і діям, що входять до лівих і правих частин продукцій. Якщо є продукція А→В, то від вершини А до вершини В йде орієнтована дуга. Якщо є продукція А, В→С, до дуги (АС) та (ВС) зв’язані відношенням „І” (кон’юнкції).

7.5.3. Схема роботи експертної системи на базі продукцій

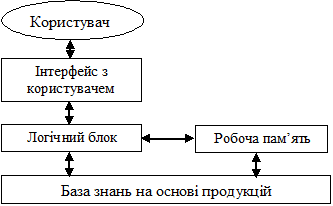
До робочої пам’яті заносяться факти від користувача, а також його запити. Логічний блок зіставляє цю інформацію з правилами із бази знань, і використовує ті правила, що можуть бути зіставлені зі вмістом робочої пам’яті.

Наприклад, продукції А→В і В→С виконуються, якщо стає відомо про істинність А.