Обмеження глибини перебору
Метод перебору
Метод повного перебору – це очевидний і універсальний метод вирішення оптимізаційних задач, якщо множина допустимих рішень М обмежена. Метод є точним, тобто гарантує оптимальний розв’язок. Недолік перебору – для практичних задач кількість варіантів надто велика. Іноді можна пожертвувати точністю розв’язку і знайти субоптимальне рішення за рахунок значного зменшення часу розрахунку. В цьому полягає суть евристичних алгоритмів.
Евристичний пошук
Евристичний пошук – процедура систематизованого перебору варіантів. Загальна схема:
- Вибрати певну дію з області можливих дій
- Здійснити дію, що приведе до зміни ситуації.
- Оцінити нову ситуацію.
- Якщо досягнуто успіху – кінець, інакше повернутися на крок 1.
Одним з важливих варіантів евристичного пошуку є метод послідовних поліпшень.
3.2.1. Експоненційна складність евристичного пошуку
Задача про виконуваність булевого виразу: для будь-якого виразу від n змінних знайти хоча б один набір значень (x1, … xn), для якого вираз приймає значення 1. Таку задачу можна розглядати як задачу пошуку на певному дереві перебору. Кожна вершина цього дерева відповідає певному набору встановлених значень x1, …xk. Ми можемо встановити змінну xk+1 в 0 або в 1, тобто маємо вибір з двох дій. Тоді кожній з цих дій відповідає одна з двох дуг, які йдуть від цієї вершини. Тобто вершина (x1, …xk) має двох нащадків (x1, …xk, 0)і (x1, …xk, 1).
При n=3 дерево перебору /можливостей/ матиме вигляд (рис.1).
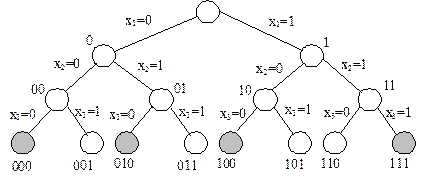
Рис.1. Дерево перебору, зафарбовані вершини відповідають виразу (х1х2) = х3
Якщо n=3, дерево має 23=8 листів. Тобто число варіантів експоненційно залежить від n (2n=exp(n ln2). Не кожний перебірний алгоритм є експоненційним (алгоритм пошуку максимального елемента в масиві – лінійний).
3.2.2. Пошук у глибину і в ширину
Є дві основні стратегії пошуку потрібної вершини на дереві:
1) пошук у ширину;
2) пошук у глибину (перебір з поверненнями, бектрекінг).
Процедура пошуку у ширину передбачає аналіз на кожному кроці нащадків усіх вершин (паралельна перевірка всіх можливих альтернатив).
Процедура пошуку в глибину передбачає першочерговий аналіз нащадків тих вершин, що були проаналізовані останніми. Всі альтернативи аналізуються послідовно; аналіз деякої альтернативи завершується лише тоді, коли встановлюється, приводить вона до успіху чи ні.
Пошук в глибину (більш поширений) дозволяє зекономити пам’ять, оскільки при його реалізації не потрібно запам’ятовувати все дерево.
3.2.3. Простір задач і простір станів
При плануванні в просторі станів заданим вважається деякий набір станів (ситуацій). Відомі дії, які може здійснювати система та які визначають перехід з одного остану в інший.
Графом станів задачі називається орієнтований граф, вершини якого відповідають можливим станам предметної області, а дуги – методам переходу від стану до стану.
Дуги можуть мати мітки, які інтерпретуються як вартість або довжина відповідного переходу. Тоді вирішення задачі являє собою пошук шляху від початкового стану до цільового; при цьому типовою вимогою є оптимізація даного рішення (пошуку найкоротшого шляху).
Планування в просторі задач передбачає декомпозицію початкової задачі на підзадачі, поки не буде досягнути зведення до задач, для яких вже готові алгоритми рішення. Таку декомпозицію можна уявити у вигляді І/АБО графа.
3.2.4. Автоматний спосіб задання алгоритму
В комп’ютері вхідна послідовність бітів перетворюється у вихідну за допомогою логічних схем. Логічні схеми поділяються на комбінаційні схеми і схеми з пам’яттю (скінченні автомати). У комбінаційних схемах значення вихідних змінних залежать лише від стану вхідних і не залежать від поточного стану схеми. Будь-яка комбінаційна схема реалізує булеву (0/1) функцію від своїх вхідних змінних. Скінчений автомат є перетворювачем, вихід якого залежить від входу, але й від поточного стану автомата.
Найуніверсальнішою моделлю комп’ютерних обчислень є машина Тьюринга. Автомати мають пам’ять у вигляді стрічки і пристрій для читання з неї. Стрічка розбита на квадрати з символами. Автомат розглядає символи по черзі, виконує обчислення і розв’язує задачі.
Формально скінчений автомат описується так: FA=<Q, A, b, q0, F>
де Q=(q1, q2, …, qn) - скінченна множина станів керування; A=(a1, a2, .., am) - вхідний алфавіт; b: Q*A→Q - функція переходів; q0 - початковий стан; 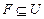 - множина станів керування.
- множина станів керування.
Приклад. Потрібно побудувати скінчений автомат який допускає тільки послідовності 0/1, при цьому в послідовності розпізнавання кількість одиниць повинна бути парною, а нулів – непарною. Згідно з умовою задачі А складатиметься з символів 0, 1, #, де # позначатиме довільний символ, відмінний від 0 і 1. Тобто, А=<0, 1, #>.
Множину станів виберемо так: Q=(q1, q2, …, q5),
де q0 - початковий стан;
q1 - стан помилки;
q2 - кількість нулів непарна, а одиниць – парна;
q3 – кількість нулів і одиниць непарна;
q4 – кількість нулів і одиниць парна;
q5 – кількість нулів парна, а одиниць – непарна;
Згідно з умовою задачі F=<q2>.Функції переходів визначаються так:
| q0#→q1 | q00→q2 | q30→q5 |
| q1#→q1 | q01→q5 | q31→q2 |
| q2#→q1 | q10→q1 | q40→q2 |
| q3#→q1 | q11→q1 | q41→q5 |
| q4#→q1 | q20→q4 | q50→q3 |
| q5#→q1 | q21→q3 | q51→q4 |
3.3. Складність алгоритмів
Універсальним обчислювальним пристроєм називатимемо пристрій, на якому можна промоделювати роботу машини Тьюринга. Машини Тьюринга дозволяють обчислювати тільки рекурсивні функції. Частково рекурсивні функції – визначені не при всіх значеннях аргумента.
Теза Тьюринга: Клас функцій, частково обчислюваних за Тьюрингом, збігається з класом частково рекурсивних функцій.
Моделі РАМ і РАСП
Машина Тьюринга дуже незручна для програмування через послідовний доступ до комірок пам’яті (стрічка), неструктурованість записів на стрічці та ін. Модель РАМ – довільний доступ до пам’яті, одна стрічка – для читання, друга – для запису. РАСП – програма перебуває в регістрах і може сама себе змінювати.
Під складністю алгоритму розуміється часова оцінка його роботи або ємність необхідної пам’яті. Апріорний аналіз алгоритму – теоретично, тестування – практична перевірка.
Розмірність задачі (вхідних даних) – це число (ціле), яке характеризує розмір вхідних даних задачі (розмірність одномірних, двомірних масивів, ...). Часова складність алгоритму – час вирішення проблеми у залежності від розмірності задачі. Асимптотична часова складність – поведінка часової складності при збільшенні розмірності задачі.
При аналізі алгоритмів використовують такі позначення.
Запис f(n)=O(g(n)) означає: функція має порядокg(n) тоді, існують дві додатні константи с i n0, що f(n)<=c[g(n)] для всіх n>n0.
Звичайно f(n)=O(g(n))визначає час обчислень; 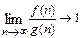 .
.
Теорема. Якщо A(n)=amnm + … a1n + a0 є поліномом ступеня m, тоді A(n)=O(nm).
Нехай є два алгоритми з часовою оцінкою обчислень O(n) і O(n2). Час виконання першого алгоритму - c1n, а другого - c2n2 (с - константи). Тоді при n<c1/c2 перевагу має перший алгоритм, а при n>c1/c2 – другий.
Найбільш типові часові оцінки алгоритмів: O(1) - константна, O(log n) -логарифмічна, O(n) -лінійна, O(nm) -поліноміальна, O(2n) -експоненційна. Для досить великих n:
O(1) < O(log n) < O(n) < O(n log n) < O(n2) < O(n3) < O(2n)
Ω(g(n)) - мінінімальна часова оцінка.
Задачі класу P I NP
Якщо розмірність задачі n, то P задача може бути розв’язана за поліноміальний час O(nm).
Задача NP може бути вирішена за поліноміальний час для недетермінованої машини Тьюринга (така машина породжує на кожному кроці певну кількість нових машин).
3.3.1. Планування в просторі станів. Основні поняття теорії графів
Граф – сукупність вершин і дуг. Для комп’ютерного опису графу використовуються: матриця інцидентності, матриця суміжності та списки суміжності. Поширена структура даних в програмуванні – лінійні списки. Лінійний список – скінченна послідовність однотипних елементів (певної довжини). Списки бувають однозв’язні (лінійні), двозв’язні (циклічні) і т.п. Лінійний список L, що складається з l1, l2,.. ln елементів , записується у вигляді L=< l1, l2,.. ln >
Існує два основних методи задання списків: послідовний (масиви) і зв’язний (динамічні змінні). Стек – список, в якому занесення і видалення елементів можна проводити тільки через один початковий елемент (вершину стеку). Стек працює за принципом: останній зайшов – перший вийшов (Last In First Out - LIFO)
Чергою називають список, в якому всі вставки здійснюються в кінець списку, а всі видалення відбуваються з голови (початку) списку.
Черга працює за принципом : перший зайшов – перший вийшов (First In First Out - FIFO).
Поняття граф ввів у 1736 році Ейлер. Граф G містить дві множини G=(V,E), де V - множина вершин (вузлів 1...n), E - множина ребер. Коли пари вершин впорядковані - то граф орієнтований, інакше - неорієнтований. Впорядкована пара позначається <i,j>, невпорядкована – (i,j). У зважених графах кожне ребро має вагу.
Ступенем вершини називається число суміжних вершин. В орієнтованому графі виділяють півстепінь входу (число вхідних ребер) та півстепінь виходу (число вихідних ребер).
Шляхом називається послідовність вершин між двома вершинами p і q.
Циклом називається шлях, у якого початкова і кінцева вершини збігаються.
Граф називається зв’язним, якщо для довільної пари вершин існує між ними шлях.
3.3.2. Способи задання графів
Існує послідовний і зв’язний спосіб задання графів. Послідовна форма використовує квадратну таблицю (Graf(n,n), n - вершин), яку називають матрицею суміжності. Якщо є зв’язок між вершинами, то Graf(I,j)=1, інакше Graf(I,j)=0. Матриця інцидентності відображає зв’язок n вершин за допомогою m дуг, розмір матриці інцидентності (n*m), але вона менш зручна, ніж матриця суміжності. Інша форма задання графу – список зв’язності.
Дерева
Дерево – це орієнтований ациклічний граф, для якого виконуються такі умови:
1) існує одна вершина, в яку не входить жодне ребро (корінь);
2) у будь-яку вершину, крім кореня, входить лише одне ребро;
3) з кореня можна знайти унікальний шлях до кожної вершини дерева.
Орієнтований граф з кількох вершин – ліс. Бінарне дерево – кожна вершина має два нащадки. При пошуку певного вузла у дереві використовують пряме і зворотне проходження вузлів.
Довільне дерево <V, T> неорієнтованого графу G=<V, E> називається остовим. Ейлеревими називають шляхи, які проходять через кожне ребро графу один раз. Якщо початковий вузол є кінцевим, то такий граф називається ейлеревим циклом. Задача про Кенігсбергські мости.
Теорема. У графі існує ейлерів шлях тільки тоді, коли граф зв’язний і містить не більше двох вершин непарного ступеня.
3.4. Загальна схема алгоритму Харта, Нельсона і Рафаеля
Узагальненням алгоритмів пошуку найкоротшого шляху на графах є алгоритм Харта, Нельсона і Рафаеля. Введемо такі позначення:
s - початкова вершина;
q - цільова вершина;
c(i,j) - довжина ребра між вершинами і та j;
d(i, j) - довжина найкоротшого шляху між і-ю та j-ю вершинами;
g(n) - довжина найкоротшого шляху між від початкової вершини до n-ї;
h(n) - довжина найкоротшого шляху між від n-ї вершини до цільової;
f(n) - довжина найкоротшого шляху між від початкової вершини до цільової, які проходять через вершину n, при цьому f(n)=g(n)+h(n);
g*(n) – оцінка довжини найкоротшого шляху між від початкової вершини до n-ї;
h*(n) – евристична функція, яка задає оцінку довжини найкоротшого шляху між від n-ї вершини до цільової;
f*(n)=g*(n)+h*(n) - оцінка f(n);
L(n) - множина всіх наступників вершини n.
Введемо робочі множини: OPEN I CLOSE. Загальна схема пошуку найкоротшого шляху:
1. Сформувати штраф пошуку G, який спочатку складається з початкової вершини s. Занести s до OPEN. Прокласти g*(s)=g(s)=0.
2. Сформувати множину CLOSE, яка спочатку буде порожня.
3. Якщо множина OPEN порожня, то вихід – потрібного шляху не існує;
4. Взяти з множини OPEN перший елемент m (відповідно до порядку, встановленого кроком 9), вилучити m з OPEN та занести її до CLOSE.
5. Якщо m - цільова вершина, то успіх. Відновити шлях від s до m на основі вказівників, що встановлені на кроках 6-8 і завершити алгоритм.
6. Розкрити вершину m, отримати множину наступників L(m). Додати до графу G всі вершини, які належать L(m), але не належать G, разом з відповідними дугами. Додати ці вершини до OPEN. Для кожної вершини 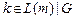 обчислити оцінки f*(k)=g*(k)+h*(k), поклавши g*(k)=g*(m)+c(m,k), встановити з k до m відновлюючий вказівник;
обчислити оцінки f*(k)=g*(k)+h*(k), поклавши g*(k)=g*(m)+c(m,k), встановити з k до m відновлюючий вказівник;
7. Для кожної вершини n з тих, які потрапили до L(m), але вже належали OPEN або CLOSE, переобчислити оцінки g*(n)=min((g*(m)+c(m,n), g*(n)). Якщо оцінка зменшилася, то перевстановити з неї відновлюючий вказівник до m.
8. Для всіх вершин з L(m), які до цього знаходилися в CLOSE, перевстановити відновлюючи вказівними для кожного з наступників цих вершин у напрямі найкоротшого шляху.
9. Перевпорядкувати множину OPEN за зростанням значень f*.
10. Повернутися на крок 3.
Якщо евристична функція не використовується, тобто h*(n)=0 і f*(n)=g*(n), то отримується алгоритм Дейкстри. Якщо взяти g*(n)=0, утворюється алгоритм Дорана і Мічі.
3.4.1. Планування в просторі задач. І-АБО граф
Планування в просторі задач полягає в розбитті задачі на підзадачі, поки під задача не зведеться до елементарної (для якої існує готовий алгоритм розв’язку). Для планування в просторі задач традиційно використовують І-АБО графи. І-АБО графом називають орієнтований граф, вершини якого відповідають задачам, а дуги – відношенням між задачами.
3.4.2. Метод „Поділяй і пануй”
Нехай потрібно вирішити задачу для елементів масиву початкових даних від p до q. Метод „поділяй і пануй”, або поділ на підзадачі, можна записати у вигляді рекурсивної процедури SubTask. Булeва функція Small(p, q) визначає, чи не зведена під задача до елементарної. Якщо задача елементарна, то знаходиться її розв’язок за допомогою функції G(p,q). Якщо задача не елементарна, то вона ділиться на дві частини функцією Divide(p,q). ПроцедураCombine рекурсивно викликає на виконання процедуру SubTask (для меншої розмірності вхідних даних).
3.5. Жадібні алгоритми
3.5.1. Види жадібних алгоритмів
Жадібні алгоритми відносяться до оптимізаційних методів і полягають в послідовному локальному поліпшенні розв’язку задачі.
3.5.2. Градієнтний метод
Одним з прикладів жадібних алгоритмів є градієнтний метод. Він використовується, якщо допустима множина розв’язку D=Rn (n - розмірний евклідовий простір), а цільова функція диференційована. Градієнтом функції у точці х=(x1 .. xn) називається вектор
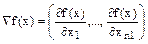 .
.
Градієнт задає задає напрямок найшвидшого зростання функції. Тоді у градієнтному методі 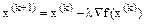 , де k – номер ітерації,λ - величина кроку у напрямку антиградієнта.
, де k – номер ітерації,λ - величина кроку у напрямку антиградієнта.
Аналогія – знайти найвищу точку на горбистій місцевості із зав’язаними очима. Досягається локальний, а не глобальний екстремум.
3.5.3. Алгоритм Пріма
Для графа G=<V, E> задані ваги його ребер. Остовим деревом графу G є неорієнтоване дерево T=<V, E/>, яке містить всі вершини графу . Вартість остового дерева визначається як вартість його ребер. Алгоритм Пріма полягає в знаходженні остового дерева мінімальної вартості. Остове дерево будують крок за кроком, додаючи до нього по одному ребру за певним оптимізаційним критерієм. Побудова дерева починається з ребер, що мають мінімальну вартість. На черговому кроці вибирається ребро, що приводить до мінімального збільшення суми вартостей ребер дерева без циклу. Процес побудови закінчується, якщо дерево Т містить всі вершини.
Алгоритм Краскала
Алгоритм Краскала відрізняється від алгоритму Пріма тим, що одночасно будується не одне остове дерево, а кілька дерев одночасно (ліс). По мір зростання окремих дерев вони об’єднуються в спільне остове дерево. Нові вершини можуть приєднуватися тільки до активних вершин (голови купи). Розглянемо роботу алгоритму Краскала до графу:

Послідовність кроків побудови остового дерева
| Голова купи | Остовий ліс | Дія | Результуюче дерево |
| (V1, V5) | {V1, V5} | додати | {V1,V5}, {V2}, {V3}, {V4}, {V6} |
| (V3, V5) | {(V1, V5) (V3, V5)} | додати | {V1, V3, V5}, {V2}, {V4}, {V6} |
| (V3, V6) | {(V1, V5) (V3, V5) (V3, V6)} | додати | {V1, V3, V5, V6}, {V2}, {V4} |
| (V5, V6) | {(V1, V5) (V3, V5) (V3, V6)} | залишити | {V1, V3, V5, V6}, {V2}, {V4} |
| (V2, V4) | {(V1,V5) (V3,V5) (V3,V6), (V2,V4)} | додати | {V1, V3, V5, V6}, {V2, V4} |
| (V1, V4) | {(V1,V5) (V3,V5) (V3, V6) (V2,V4) (V1, V4)} | додати | {V1, V3, V5, V6, V2, V4} |
3.5.4. Динамічне програмування
Динамічне програмування – це такий алгоритмічний метод, коли рішення задачі є результатом певної послідовності розв’язків. Метод побудований на послідовному аналізі варіантів. На кожному кроці відкидаються розв’язки, серед яких не може бути оптимального, і таким чином множина конкурентоспроможних варіантів стискується.
В динамічному програмуванні обробляється одночасно послідовність рішень, серед яких повинне бути оптимальне. Послідовність поступово звужується. В динамічному програмуванні використовують рекурентні рівняння.
3.6. Вирішувані інтелектуальних задач
Вирішував інтелектуальних задач – штучна система, яка сприймає формалізований опис деякої задачі і на основі його розробляє план рішення.
3.6.1. Загальний вирішував задач
В кінці 50-х й на початку 60-х розвивалася програма „Загальний вирішував задач” (GPS). В рамках цієї програми створено програму „Логік-теоретик” (А.Ньюелл, Г.Саймон, Дж. Шоу) для доведення теорем математичної логіки (генерація гіпотези й перевірка її істиності).
Схема прийняття рішення наступна:
- Проаналізувати поточну ситуацію.
- Порівняти ситуацію з бажаною; якщо відмінностей немає – кінець роботи.
- З’ясувати, які оператори можна застосувати для зменшення існуючої різниці.
- Послідовно застосовувати знайдені оператори.
- Повернутися на крок 1.
3.6.2. Ігрові задачі як задачі прийняття рішень
Ігрові задачі – планування цілеспрямованих дій і прийняття рішень. Характерна особливість ігрових задач – наявність суперника. Теорія ігор – математична дисципліна, яка вивчає аспекти поведінки учасників конфліктних ситуацій та має на меті виробити оптимальні для кожного з них стратегії (засоби досягнення цілей). Конфліктною називають ситуацію, коли гравці мають різні цілі (різні функції виграшу).
3.6.3. Основи теорії однокрокових ігор
Нехай грають два гравця А і В.
Гравець А може вибрати одну з m стратегій αi, i=1..m.
Гравець В може вибрати одну з n стратегій βj, j=1..n, .
Обидва гравці здійснюють свій вибір одночасно, після чого гравець В платить гравцю А суму rij, яка залежить від обраних стратегій. Оскільки виграш одного гравця дорівнює програшу іншого, сума виграшів двох гравців дорівнює нулю і така гра називається грою з нульовою сумою або антагоністичною. Одно крокові антагоністичні ігри характеризуються матрицею виграшів, елементи якої дорівнюють виграшам одного з гравців (А).
3.6.4. Позиційні ігри з оптимальними стратегіями
Досить дослідженими є позиційні ігри двох осіб: шахи, шашки, „хрестики-нолики”... .За правилами гри кожен гравець по черзі робить свій хід. Ці ігри є детермінованими і з повною інформацією, відносяться до скінченних антагоністичних ігор. Базою теорії ігор вважається результат Льюїса і Райфа: для кожного гравця у будь-якій позиції існує оптимальна стратегія, тобто алгоритм визначення чергового ходу, що призведе до оптимального результату.
Ключовим поняттям в теорії позиційних ігор є дерево гри (дерево аналізу):
1. Кожна вершина дерева відповідає окремій позиції.
2. Корінь дерева відповідає позиції, що аналізується.
3. Листки дерева відповідають завершальним позиціям з відомою функцією виграшу.
4. Дуги відповідають ходам.
Суперники традиційно носять імена α і β. За домовленістю вважається, що правило вибору ходу в початковій позиції належить гравцеві α. Вершини, в яких право ходу належить α, називають α-вершини; відповідно називають β-вершини.
За домовленістю стандартний хід в шахах, шашках і т.д. вважається півходом, а хід складається з ходу гравця і відповіді суперника. Дерево гри може бути експліцитним (задається явно) й імпліцитним (породжується по мірі необхідності).
Розрахуємо кількість позицій для гри в шахи. Якщо на кожному кроці можна зробити 30 ходів, а партія складається з 80 півходів, то кількість позицій 3080.
Обмеження глибини перебору
Для обмеження перебору звичайно зменшують глибину перебору d. Горизонтом для даної позиції називають множину позицій для глибини d.
На горизонті отримуються абсолютно завершальні (оцінка позиції визначена) та відносно завершальні позиції. Для відносно завершальних позицій вводяться статичні оціночні функції, які оцінюють отриману ситуації без врахування динаміки. Наприклад, для шахів враховується кількість та вид фігур, їх розміщення та ін.
В шашках статична оцінка може бути обчислена як функція 6k+4m+u, де k - перевага в дамках, m - у простих шашках, u - перевага в рухливості.
3.6.5. Альфа – бета відтинання
Альфа-бета відтинання є одним зі способів скорочення перебору. Відтинанням у деякій вершині називається припинення аналізу цієї вершини разом з усіма її наступниками.
Базова ідея відтинань наступна: якщо деякий хід досягає максимально можливого виграшу, то інші його альтернативи не розглядаються. З кожною вершиною зв’язується попередня оцінка, яка змінюється у ході аналізу її наступників. Перед початком аналізу попередня оцінка альфа-вершини дорівнює - ∞, а бета-вершини +∞. Після завершення аналізу всіх наступників попередня оцінка набуває остаточного значення, тобто стає остаточною оцінкою.
Попередня оцінка альфа-вершини дорівнює максимуму з остаточних оцінок безпосередніх наступників. Попередня оцінка бета-вершини дорівнює мінімуму з остаточних оцінок безпосередніх наступників.
Правила відтинань:
- Відтинання у альфа-вершині відбувається, коли попередня оцінка цієї вершини стає не меншою, ніж попередня оцінка будь-якого бета-попередника.
- Відтинання у бета-вершині відбувається, коли попередня оцінка цієї вершини стає не більшою, ніж попередня оцінка будь-якого альфа-попередника.
| <== предыдущая лекция | | | следующая лекция ==> |
| Метод допустимих перетворень | | | Навчання нейронних мереж |
Дата добавления: 2016-04-19; просмотров: 2048;
