Навчання нейронних мереж

Штучний нейрон

Основними компонентами нейромережі є нейрони /neurons/ (елементи, вузли), які з’єднані зв’язками. Сигнали передаються по зваженим зв’язкам(connection), з кожним з яких пов’язаний ваговий коефіцієнт (weighting coefficient) або вага. Моделі НМ – програмні і апаратні, найбільш поширені – програмні. Використання – розпізнавання образів, прогнозування...

На вхід штучного нейрона поступає множина сигналів, які є виходами інших нейронів. Кожен вхід множиться на відповідну вагу, аналогічну його синаптичній силі, і всі виходи підсумовуються, визначаючи рівень активації нейрона. На рис.1 представлена модель, що реалізує цю ідею. Хоча мережеві парадигми досить різноманітні, в основі майже всіх їх лежить ця конфігурація. Тут множина вхідних сигналів, позначених x₁, x₂,…, x_n, поступає на штучний нейрон. Ці вхідні сигнали, в сукупності позначаються вектором X, відповідають сигналам, що приходять в синапси біологічного нейрона. Кожен сигнал множиться на відповідну вагу w₁, w₂,…, w_n, і поступає сумуючий блок, позначений Σ. Кожна вага відповідає «силі» одного біологічного синаптичного зв'язку (множина ваг в сукупності позначається вектором W). Сумуючий блок, який відповідає тілу біологічного нейрона, складає зважені входи алгебраїчно, створюючи вихід, який ми називатимемо NET. У векторних позначеннях це може бути компактно записано: NET = XW.

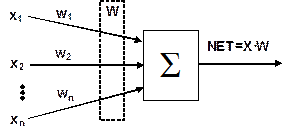
Рис. 1. Штучний нейрон

4.3. Активаційні функції

Сигнал NET далі, як правило, перетворюється активаційною функцією F і дає вихідний нейронний сигнал OUT = F(NET). Активаційна функція F(NET) може бути:

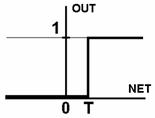
1. Пороговою бінарною функцією (рис.2а)

,

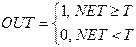де Т - деяка постійна порогова величина, або ж функція, що точніше моделює нелінійну передавальну характеристику біологічного нейрона.

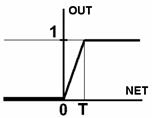
2. Лінійною обмеженою функцією (рис.2б)

.

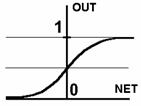
3. Функцією гіперболічного тангенса(рис.2в)

.

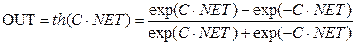де С > 0 – коефіцієнт ширини сигмоїди по осі абсцис (звичайно С=1).

4. Сигмоїдною (S-подібною) або логістичною функцією (рис.3г)

,

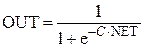З виразу для сигмоїда очевидно, що вихідне значення нейрона лежить в діапазоні [0,1] (рис.4). Популярність сигмоїдної функції зумовлюють наступні її властивості:

· здатність підсилювати слабкі сигнали сильніше, ніж великі;

· монотонність і диференційованість на всій осі абсцис;

· простий вираз для похідної

.

а) б) в) г)

Рис. 2. Вид функцій активації: а) порогова бінарна функція; б) лінійна обмежена функція; в) гиперболічний тангенс; г) сигмоїд

4.4. Одношарові нейронні мережі

Проста мережа складається з групи нейронів, створюючих шар (рис. 3). Кожен елемент з множини входів Х окремою вагою сполучений з кожним штучним нейроном. Кожен нейрон видає зважену суму входів в мережу. У штучних і біологічних мережах багато з'єднань можуть бути відсутніми, можуть мати місце також з'єднання між виходами і входами елементів в шарі.

Рис. 3. Одношарова НМ

Зручно вважати вагу елементами матриці W. Матриця має m рядків і n стовпців, де m - число входів, а n - число нейронів. Наприклад, w_3,2 - це вага, що пов'язує третій вхід з другим нейроном. Таким чином, обчислення вихідного вектора Y, компонентами якого є виходи OUT нейронів, зводиться до матричного множення Y = XW, де Y і Х - вектори-рядки.

4.5. Персептрони і зародження штучних нейромереж

Перше систематичне вивчення штучних нейронних мереж було зроблене Мак-Каллоком і Піттсом в 1943 р. В роботі вони досліджували мережеві парадигми для розпізнавання зображень, що піддаються зсувам і поворотам. Проста нейронна модель (рис. 4) використовувалася в більшій частині їх роботи. Елемент Σ множить кожен вхід х на вагу w і підсумовує зважені входи. Якщо ця сума більше заданого порогового значення, вихід рівний одиниці, інакше - нулю. Ці системи одержали назву персептронів. Вони складаються з одного шару штучних нейронів, сполучених за допомогою вагових коефіцієнтів з множиною входів (рис. 4).

Перші персептрони були створені Ф.Розенблатом у 60-х роках. Первинна ейфорія змінилася розчаруванням, коли виявилося, що персептрони не здатні навчитися рішенню ряду простих задач. М.Мінський строго проаналізував цю проблему і показав, що є жорсткі обмеження на те, що можуть виконувати одношарові персептрони. Відкриття методів навчання багатошарових мереж вплинуло на відродження інтересу до нейромереж.

Рис. 4. Персептрон

Навчання персептрона:

1. Ініціалізація вагових матриць W (випадкові значення)

2. Подати вхід X і обчислити вихід Y для цільового вектора Y^T

3. Якщо вихід правильний – перейти на крок 4; інакше обчислити різницю D = Y^T – Y;модифікувати ваги за формулою: w_ij(e+1) = w_ij(e) + α D Х_і,

де w_ij(e) - значення ваги від нейрона i до нейрона j до налагодження, w_ij(e+1) - значення ваги після налагодження, α - коефіцієнт швидкості навчання, Х_i - вхід нейрона i, e – номер епохи (ітерації під час навчання).

4. Виконувати цикл з кроку 2, поки мережа не перестане помилятися. На другому кроці у випадковому порядку пред’являються всі вхідні вектори.

4.6. Багатошарові нейронні мережі

Багатошарові мережі (рис. 5) володіють значно більшими можливостями, ніж одношарові. Проте багатошарові мережі можуть привести до збільшення обчислювальної потужності в порів­нянні з одношаровими лише в тому випадку, якщо активаційна функція буде нелінійною.

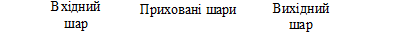
Рис. 5. Багатошарова НМ

Навчання нейронних мереж

Мережа навчається, щоб для деякої множини входів X давати бажану множину виходів Y. Навчання здійснюється шляхом послідовного пред'явлення вхідних векторів з одночасним налагодженням ваг відповідно до певної процедури. Розрізняють алгоритми навчання з вчителем і без вчителя, детерміновані і стохастичні.

Навчання з вчителем.Навчання з вчителем припускає, що для кожного вхідного вектора X існує цільовий вектор Y^T, що є необхідним виходом. Разом вони називаються навчальною парою. Звичайно мережа навчається для навчальної множини. В ході навчання зчитується вхідний вектор X, обчислюється вихід мережі Y і порівнюється з відповідним цільовим вектором Y^T, різниця D ~ Y^T – Y за допомогою зворотного зв'язку подається в мережу і змінюються ваги W відповідно до алгоритму, прагнучого мінімізувати помилку ε.

Навчання без вчителя. Незважаючи на прикладні досягнення, навчання з вчителем критикувалося за свою біологічну неправдоподібність. Навчальний алгоритм при навченні без вчителя налагоджує вагу мережі так, щоб виходили узгоджені вихідні вектори, тобто щоб пред'явлення досить близьких вхідних векторів давало однакові виходи. Процес навчання виділяє статистичні властивості навчальної множини і групує схожі вектори в класи.

Більшість сучасних алгоритмів навчання походить з концепцій Хебба. Ним запропонована модель навчання без вчителя, в якій синаптична сила (вага) зростає, якщо активовані обидва нейрони, джерело і приймач. У штучній нейронній мережі, що використовує навчання по Хеббу, нарощування ваг визначається добутком рівнів збудження передаючого і приймаючого нейронів:

w_ij(e+1) = w(e) + α OUT_i OUT_j,

де w_ij(e) - значення ваги від нейрона i до нейрона j до налагодження, w_ij(e+1) - значення ваги від нейрона i до нейрона j після налагодження, α - коефіцієнт швидкості навчання, OUT_i - вихід нейрона i та вхід нейрона j, OUT_j - вихід нейрона j; e – номер епохи (ітерації під час навчання).