Алгоритм зворотного розповсюдження помилки (backpropagation)
Зворотне розповсюдження помилки означає, що сигнали помилки з виходу мережі використовуються для корекції ваг попередніх шарів. Розглянемо структуру 3-шарової НМ.
1. Вхідний шар X;стани його елементів записані у векторі vXi;деi=1..QX.Розмір навчальної множини(кількість векторів) на входіХдорівнює Qn,номер вектора n=1..QN.
2. Приховані шари
Шар V1 (рівень L=1):векторV1k1;де k1=1..QV1; матриця ваг W1i,k1; різниця векторів D1k1;
Шар V2 (L=2): векторV2k2; де k2=1..QV2; матриця ваг W2k1,k2; різниця D2k2;
3. Вихідний шар (L=3): стани його елементів записані у векторі Yj; j=1..QY; матриця ваг W3k2,j; різниця D3j; істинний вихід (true) описується вектором YTj; j=1..QY.
Тобто Ytj – істинне значення для елементу j, Yj- його реальних вихід.
Розмір навчальної вибірки на виході Y: QM, номер вектораm=1..QM.
Навчання нейромережі відбувається за наступним алгоритмом (рис.10)
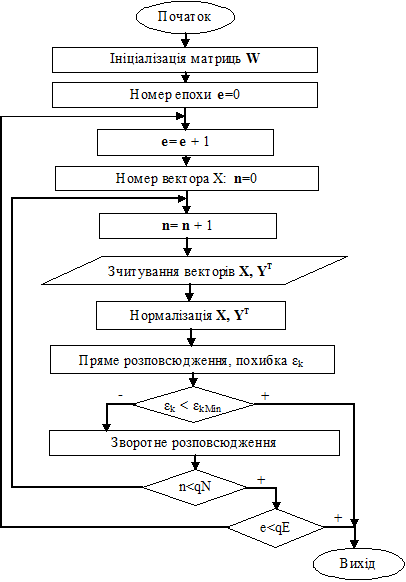
Рис. 6. Алгоритм навчання нейромережі зі зворотним розповсюдженням помилки
1. Ініціалізація.Початкові вагові коефіцієнти W приймаються рівними малим випадковим значенням, наприклад з діапазону [-0.3, .... +0.3]:
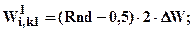
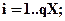
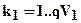 , ΔW=0,3.
, ΔW=0,3.
2. Нормалізація (масштабування) значень всіх векторів X, YТ(для кожного типу окремо) в діапазон (MinN; MaxN), наприклад MinN=0,1; MaxN=0,9;

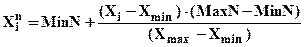
3. Пряме розповсюдження (Direct)полягає у знаходженні вихідного вектора Y на основі вхідного X за наступними формулами.
Шар 1: 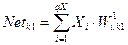 ;
; 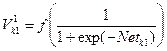 , де
, де 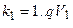
Шар 2: 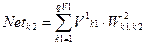 ;
; 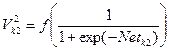 , де
, де 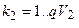
Шар 3: 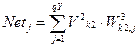 ;
; 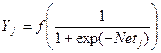 , де
, де 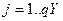
В результаті прямого розповсюдження можна обчислити помилки навчання мережі:
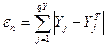 - лінійна помилка для вектора n
- лінійна помилка для вектора n
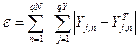 - лінійна помилка для всіх векторів навчальної множини
- лінійна помилка для всіх векторів навчальної множини
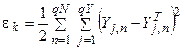 - сумарна квадратична помилка (для всіх векторів).
- сумарна квадратична помилка (для всіх векторів).
4. Зворотнє розповсюдження помилки (backpropagation)полягає у корекції вагових коефіцієнтів через сигнал різниці D.
3 шар. 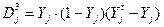 ,
, 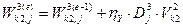 , де
, де 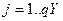 , e - номер епохи; оскільки в якості активіаційної функції використовується сигмоїдна, тому різниця векторів (YT-Y) множиться на похідну від сигмоїдної функції: Y(1 – Y) .
, e - номер епохи; оскільки в якості активіаційної функції використовується сигмоїдна, тому різниця векторів (YT-Y) множиться на похідну від сигмоїдної функції: Y(1 – Y) .
2 шар. 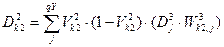 ,
, 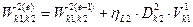 , де
, де 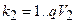
1 шар.  ,
, 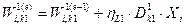 , де
, де 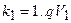 ,
,
ηY, ηL2, ηL1 - норми навчання (значення норми навчання, наприклад, 0,5).
Дані для нейронної мережі можна поділити наступним чином:
1. Навчання (відомі вхідні і вихідні дані, визначити вагові коефіцієнти)
2. Тестування (відомі вхідні і вихідні дані, порівняти розраховані вихідні дані з істинними)
3. Діагностика (реальне визначення результатів за вхідними даними)
4.9. Мережі зустрічного розповсюдження. Шари Кохонена і Гроссберга
Основною перевагою НМ зустрічного розповсюдження є порівняно малий час навчання (приблизно в 100 разів менше, ніж для зворотного розповсюдження помилки). В зустрічному розповсюдженні об'єднані два добре відомих алгоритми: карта Кохонена і зірка Гроссберга.
Мережа зустрічного розповсюдження функціонує подібно до довідкового бюро. В процесі навчання вхідні вектори асоціюються з відповідними вихідними векторами. Ці вектори можуть бути двійковими або неперервними. Коли мережа навчена, обробка вхідного вектора приводить до необхідного вихідного вектора. Узагальнююча здатність мережі дозволяє одержувати правильний вихід навіть при пошкодженого вхідного вектора. Це дозволяє використовувати дану мережу для розпізнавання і відновлення образів.
Структура НМ зустрічного розповсюдження наступна (рис.11)
НОРМАЛЬНЕ ФУНКЦІОНУВАННЯ
Шари Кохоненна.У своїй простій формі шар Кохонена функціонує за принципом «переможець забирає все», тобто для даного вхідного вектора один і лише один нейрон Кохонена видає на виході логічну одиницю, всі інші видають нуль. Переможцем є нейрон з максимальним значенням вихідного сигналу 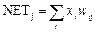 . Вихід нейронів шару Гроссберга:
. Вихід нейронів шару Гроссберга: 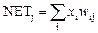 .
.
НАВЧАННЯ. Шар Кохонена класифікує вхідні вектори в групи схожих. Це досягається за допомогою такого налагодження ваг шару Кохонена, що близькі вхідні вектори активують один і той же нейрон даного шару. Задачею шару Гроссберга є отримання необхідних виходів.
4.10. Стохастичні методи
Стохастичні методи корисні як для навчання штучних нейронних мереж, так і для отримання виходу від вже навченої мережі. Стохастичні методи навчання приносять велику користь, дозволяючи виключати локальні мінімуми в процесі навчання. Є два класи повчальних методів: детерміністичний і стохастичний.
Детерміністичний метод навчання крок за кроком здійснює процедуру корекції ваг мережі, засновану на використанні їх поточних значень, а також величин входів, фактичних виходів і бажаних виходів. Зворотне розповсюдження помилки є прикладом подібного підходу.
Стохастичні методи навчання виконують псевдовипадкові зміни величин ваг, зберігаючи ті зміни, які ведуть до поліпшень. Для навчання мережі може бути використана наступна процедура:
1. Вибрати вагу випадковим чином і змінити її на невелику випадкову величину. Пред'явити множину входів і обчислити виходи.
2. Порівняти виходи з бажаними виходами і обчислити величину різниці між ними. Загальноприйнятий метод полягає в знаходженні різниці між фактичним і бажаним виходами для кожного елементу навчальної пари. Метою навчання є мінімізація цієї різниці (цільової функції).
3. Якщо зміна ваги допомагає (зменшує цільову функцію), то зберегти її, інакше повернутися до первинного значення ваги.
Повторювати кроки з 1 до 3 до тих пір, поки мережа не буде навчена достатньою мірою.
Для вирішення проблеми локальних мінімумів використовується наступний метод. Штучні нейронні мережі навчаються спочатку грубим налагодженням ваг, а потім більш точним. На першому етапі робляться великі випадкові корекції із збереженням тільки тих змін ваг, які зменшують цільову функцію. Потім середній розмір кроку поступово зменшується, і глобальний мінімум досягається. Це нагадує відпал металу, тому для опису такої методики використовують термін «імітація відпалу».
4.11. Мережі зі зворотними зв’язками, мережі Хопфілда
Одними із НМ зі зворотними зв’язками є мережі Хопфілда.
Мережі зі зворотними зв'язками мають шляхи, що передають сигнали від виходів до входів, тому відгук таких мереж є динамічним, тобто після зчитування нового входу обчислюється вихід і, передаючись по мережі зворотного зв'язку, модифікує вхід. Потім вихід повторно обчислюється, і процес повторюється знову і знову. Для стійкої мережі послідовні ітерації приводять до все менших змін виходу, поки вихід не стає постійним. Для багатьох мереж процес ніколи не закінчується, такі мережі називають нестійкими.
В першій роботі Хопфілда активаційна функція F була пороговою відносно порогу T. Вона обчислюється наступним чином:
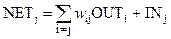 ,
,
OUT= 1, якщо NETj>Тj,
OUT = 0, якщо NETj<Тj,
OUT не змінюються, якщо NETj = Тj,
Мережа з зворотними зв’язками є стійкою, якщо її матриця симетрична й має нулі на головній діагоналі, тобто якщо wij = wji й wii = 0 для всіх i.
Людська пам'ять асоціативна, тобто деякий спогад може породжувати велику пов'язану з ним область. Наприклад, декілька музичних тактів можуть викликати цілу гамму спогадів, включаючи пейзажі, звуки і запахи. Навпаки, звичайна комп'ютерна пам'ять адресується локально.
Мережа із зворотним зв'язком формує асоціативну пам'ять. Подібно людській пам'яті по заданій частині потрібної інформації вся інформація витягується з «пам'яті». Щоб організувати асоціативну пам'ять за допомогою мережі із зворотними зв'язками, вага повинна вибиратися так, щоб утворювати енергетичні мінімуми в потрібних вершинах одиничного гіперкуба.
Хопфілд розробив асоціативну пам'ять з безперервними виходами, що змінюються в межах від +1 до -1, відповідних двійковим значенням 0 і 1. Інформація, що запам'ятовується, кодується двійковими векторами і зберігається у вагах згідно наступній формулі:
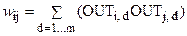
де m - число вихідних векторів, що запам'ятовуються; d - номер вихідного вектора, що запам'ятовується; OUTi,j – i-компоненту вихідного вектора, що запам'ятовується.
4.12. Адаптивна резонансна теорія
Мозок людини виконує важку задачу обробки безперервного потоку сенсорної інформації, одержуваної з навколишнього світу. З потоку тривіальної інформації він повинен виділити життєво важливу інформацію, обробити її і, можливо, зареєструвати в довготривалій пам'яті. Розуміння процесу людської пам'яті є серйозною проблемою; нові образи запам'ятовуються в такій формі, що раніше збережені не модифікуються і не забуваються. Це створює дилему: яким чином пам'ять залишається пластичною, здібною до сприйняття нових образів, і в той же час зберігає стабільність, що гарантує, що образи не знищаться і не руйнуватимуться в процесі функціонування?
Традиційні штучні нейронні мережі виявилися не в змозі розв'язати проблему стабільності-пластичності. Дуже часто навчання новому образу знищує або змінює результати попереднього навчання. В деяких випадках це не істотно. Якщо є тільки фіксований набір повчальних векторів, вони можуть пред'являтися при навчанні циклічно. У мережах із зворотним розповсюдженням, наприклад, навчальні вектори подаються на вхід мережі послідовно до тих пір, поки мережа не навчиться всьому вхідному набору. Якщо, проте, повністю навчена мережа повинна запам'ятати новий повчальний вектор, він може змінити вагу настільки, що потрібно повне перенавчання мережі.
У реальній ситуації мережа піддаватиметься діям, що постійно змінюються; вона може ніколи не побачити один і той же навчальний вектор двічі. При таких обставинах мережа часто не навчатиметься; вона безперервно змінюватиме свою вагу, не досягаючи задовільних результатів.
Більш того, в роботі є приклади мережі, в якій тільки чотири повчальні вектори, що пред'являються циклічно, примушують ваги мережі змінюватися безперервно, ніколи не сходячись. Така нестабільність є одним з головних чинників, що примусили Гроссберга і його співробітників досліджувати радикально відмінні конфігурації. Адаптивна резонансна теорія (APT) є одним з результатів дослідження цієї проблеми.
Мережею APT є векторний класифікатор. Вхідний вектор класифікується залежно від того, на якій з множини образів, раніше збережених, він схожий. Своє класифікаційне рішення мережа APT виражає у формі збудження одного з нейронів шару, що розпізнає. Якщо вхідний вектор не відповідає жодному з образів, що збережені, то створюється нова категорія. Якщо визначено, що вхідний вектор схожий на один із збережених векторів (для певного критерію схожості), то збережений вектор буде змінюватиметься під впливом нового вхідного вектора так, щоб стати більш схожим на цей вхідний вектор.
Таким чином розв'язується дилема стабільності-пластичності. Новий образ може створювати додаткові класифікаційні категорії, проте новий вхідний образ не може примусити змінитися існуючу пам'ять.
Дата добавления: 2016-04-19; просмотров: 3011;
