Построение начального допустимого базисного решения

Транспортная задача

Постановка задачи.

Важным частным случаем задачи линейного программирования является транспортная задача. Сформулируем ее в общем виде.

На m станциях отправления сосредоточено соответственно единиц однородного груза. Этот груз нужно доставить в n пунктов назначения в каждый из которых требуется соответственно единиц этого груза. Заданы стоимости перевозки единицы груза из любого пункта в любой пункт Требуется составить такой план перевозок, при котором со всех станций был бы вывезен весь груз, потребности всех пунктов были бы удовлетворены и суммарные затраты на перевозку были бы минимальны.

Естественно считать что суммарный запас груза на всех станциях равен суммарной потребности всех станций назначения, то есть

(1)

Данные задачи можно свести в таблицу перевозок:

Пункты   Станции		. . .		. . .		Запасы
		. . .		. . .
. . .	. . .	. . .	. . .	. . .	. . .	. . .
		. . .		. . .
. . .	. . .	. . .	. . .	. . .	. . .	. . .
		. . .		. . .
Потребности		. . .		. . .

Обозначим через количество единиц груза, перевозимого со станции в пункт . Тогда количество груза, которое планируется перевезти в пункт со всех станций, составит сумму

, и эта сумма равна . Получаем уравнение (2) =

С другой стороны количество груза, отправляемого со станции во все пункты , составит сумму

, и эта сумма должна быть равна .

Получаем уравнение (3) =

Записывая уравнения (2) и (3) для всех пунктов и всех станций , получим систему, содержащую m + n уравнений:

Общая стоимость всех перевозок равна сумме

Мы построили математическую модель транспортной задачи и получили задачу линейного программирования в канонической форме: среди неотрицательных решений системы линейных уравнений (4) найти такое, при котором линейная функция S достигает наименьшего значения.

Транспортная задача, для которой выполняется условие (1), называется сбалансированной (закрытой). В противном случае транспортная задача называется несбалансированной (открытой).

Далее научимся решать сбалансированную задачу. Как и любая задача линейного программирования, транспортная задача может быть решена симплекс – методом. Однако система ограничений (4) задачи имеет особенности: коэффициенты при переменных во всех уравнениях равны нулю или единице и каждая переменная входит в (4) ровно 2 раза – один раз в «горизонтальное» уравнение типа (3), другой раз в «вертикальное» уравнение типа (2). Это позволяет решить задачу симплекс–методом без симплекс–таблиц, используя только таблицу перевозок.

Прежде всего, заметим, что сбалансированная транспортная задача всегда имеет неотрицательное решение.

Теорема 1. Если выполняется условие (1), то система (4) имеет неотрицательное решение

Действительно при подстановке указанных значений переменных в любое уравнение системы (4) получается верное числовое равенство.

Так как функция S ³ 0 и непрерывна на множестве неотрицательных решений системы (4), то сбалансированная задача всегда имеет оптимальное решение. Чтобы найти это решение симплекс–методом, надо знать число базисных переменных – ранг системы (4).

Теорема 2. Ранг R системы ограничений сбалансированной транспортной задачи вычисляется по формуле: R = m + n - 1.

Доказательство. В системе (4) m + n уравнений. Если сложить почленно первые m «горизонтальных» уравнений и из полученной суммы отнять все «вертикальные» уравнения кроме последнего, то в силу равенства (1) получим последнее «вертикальное» уравнение. Это означает, что последнее уравнение системы (4) есть линейная комбинация остальных n+m-1 уравнений, значит ранг R £ m+n-1.

Теперь докажем, что ранг R ³ m+n-1. Из алгебры известно, что если некоторые k переменных системы линейных уравнений можно выразить через остальные переменные системы, то ранг такой системы не меньше k. В качестве этих m+n-1 переменных возьмем переменные, которые соответствуют клеткам первой строки и первого столбца таблицы перевозок: (6) . Для переменных найдем выражения через переменные, не входящие в (6) из соответствующих «вертикальных» уравнений (2):

Для переменных найдем выражения через переменные, не входящие в (6) из соответствующих «горизонтальных» уравнений (3):

Наконец, чтобы выразить через переменные, не входящие в список (6), воспользуемся первым «горизонтальным» уравнением

=

и подставим в него найденные выражения для переменных . Таким образом, мы выразили m+n-1 переменных из списка (6) через остальные переменные системы, поэтому ранг R ³ m+n-1. Из доказанных двух неравенств получаем, что R = m + n - 1.

Решая транспортную задачу симплекс–методом, будем вписывать значения базисных переменных построенного базисного решения в соответствующие клетки таблицы перевозок. Будем эти клетки называть базисными, а клетки, соответствующие свободным переменным, – свободными. В следующем разделе рассмотрим способы построения допустимого базисного решения сбалансированной транспортной задачи, необходимого для начала ее решения симплекс–методом.

Построение начального допустимого базисного решения

Одним из методов построения начального базисного решения системы ограничений транспортной задачи является метод «северо – западного» угла, сущность которого покажем на следующем примере.

Транспортная задача задана таблицей:

Пункты   Станции		Запасы груза на станциях
Потребности

Ранг системы ограничений этой задачи равен 3 + 4 – 1 =6. Попытаемся заполнить 6 клеток таблицы перевозок неотрицательными числами, начиная с «северо – западной» клетки, соответствующей переменной 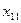, так, чтобы они в совокупности с нулевыми значениями остальных «свободных» клеток образовали базисное решение системы.

Пытаемся удовлетворить потребности первого пункта (70 единиц) запасами первой станции (100 единиц). В нашем случае это можно сделать, так как 100 > 70. Впишем в клетку 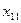число 70. Потребности первого пункта полностью удовлетворены, поэтому столбец, соответствующий первому пункту, можно временно исключить из таблицы, а запасы груза на первой станции сократились до 30 единиц.

Переменную 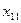можно считать базисной, так как ее можно выразить через остальные переменные, входящие в первое вертикальное уравнение, соответствующее удаляемому первому столбцу таблицы:

(8) 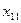= 70 – ( + +… + ).

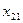Можно считать, что мы пришли к новой задаче, определяемой таблицей с тремя станциями и тремя пунктами потребления, причем она снова сбалансированная, так как сумма запасов груза на всех станциях 170 равна сумме потребностей всех оставшихся пунктов.

К новой таблице применим тот же прием и попытаемся заполнить новую «северо – западную» клетку , удовлетворяя потребности второго пункта = 40 запасами =30 первой станции. Это можно сделать лишь частично, так как 30 < 40. Поэтому впишем в клетку число 30, при этом потребности второго пункта сократятся до , а запасы первой станции окажутся исчерпанными полностью. Следовательно, из таблицы можно временно удалить первую строку, а переменную выразить из соответствующего первого горизонтального уравнения через остальные переменные , , которые можно считать свободными, а вместо переменной 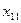подставить уже найденное для нее выражение (8) через свободные переменные. Поэтому переменную можно считать базисной.

В полученной таблице размера 2*3 снова находим «северо –западную» клетку и т. д. В результате получим следующую таблицу, в которой заполнено 6 клеток (на каждом шаге, кроме последнего – шестого, мысленно исключается столбец или строка, а на последнем сразу строка и столбец).

Пункты   Станции		Запасы груза на станциях
Потребности

Из предыдущих рассуждений следует, что последовательность чисел 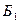= (70, 30, 0, 0, 0, 10, 60, 10, 0, 0, 0, 60) является базисным решением системы ограничений рассматриваемой задачи. Стоимость всех перевозок S = =1660.

Проведенные на примере рассуждения носят общий характер и применимы к любой сбалансированной задаче. Сформулируем в общем виде правила построения допустимого базисного решения транспортной задачи методом «северо – западного» угла:

1. Пытаемся удовлетворить потребности первого пункта запасами первой станции. При этом возможны 3 случая:

1.1) > ; 1.2) < ; 1.3) = .

В случае 1.1) потребности первого пункта можно полностью удовлетворить запасами первой станции. Вписываем в клетку 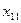число и временно исключаем из рассмотрения первый столбец таблицы. В результате приходим к более простой задаче, в которой суммарное число станций и пунктов потребления уменьшилось на единицу , причем запасы груза первой станции равны = - .

В случае 1.2) вписываем в клетку 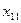число и временно исключаем из рассмотрения первую строку таблицы. В результате приходим к более простой задаче, в которой суммарное число станций и пунктов потребления опять уменьшилось на единицу, причем потребности груза первого пункта уменьшились до = - .

В случае 1.3) полагаем 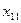= = . При этом потребности первого пункта полностью удовлетворены, и запасы первой станции полностью исчерпаны. В этом случае исключим временно из рассмотрения либо первую строку, либо первый столбец, но не то и другое вместе. Например, исключим первый столбец, а запасы груза первой станции считаем равными нулю. В результате приходим снова к более простой задаче, в которой суммарное число станций и пунктов потребления опять уменьшилось на единицу.

Во всех трех случаях вопрос об отыскании допустимого базисного решения транспортной задачи мы сводим к аналогичному вопросу для задачи, в которой суммарное число станций и пунктов потребления на единицу меньше, чем в исходной задаче.

2) Повторяем операцию, описанную в правиле 1) с «северо – западной» клеткой в полученной таблице и т.д. В результате получим допустимое базисное решение задачи.

Существенный недостаток метода «северо – западного» угла заключается в том, что он не учитывает тарифы перевозок, начиная построение базисного решения с заполнения верхней левой клетки таблицы. Однако метод допускает модификацию, лишенную этого недостатка: на каждом шаге надо выбирать для заполнения числом не «северо – западную» клетку, а клетку, имеющую минимальный тариф. При таком способе выбора базисных клеток обычно (но не всегда!) получается базисное решение с меньшей суммарной стоимостью всех перевозок, чем решение, построенное методом «северо – западного» угла.

Указанная модификация метода получила название метода «наименьшей стоимости ». Применим этот метод для построения допустимого базисного решения рассмотренной выше задачи.

Начинаем строить решение с клетки (3,2) с наименьшим тарифом, равным единице. Полагаем =min(80,40) = 40 и удаляем временно из таблицы второй столбец, полагая = 60-40 = 20. Теперь клетка с наименьшим тарифом, равным двум – клетка(2,4). В эту клетку записываем число , и, а запасы второй станции считаем равными десяти и эту строку сохраняем. Затем рассматриваем клетку (3,3) с наименьшим тарифом, равным трем и т.д. Получаем заполненную таблицу:

Пункты   Станции		Запасы груза на станциях
Потребности

Построенная по методу наименьшей стоимости система чисел

= (70, 0, 30, 0, 0, 0, 10, 70, 0, 40, 20, 0) является базисным решением системы ограничений рассматриваемой задачи. Стоимость всех перевозок S = =970, значительно меньше чем при базисном решении, полученным методом «северо – западного» угла.