Переход от одного базисного решения к другому с помощью цикла пересчета свободной клетки

Рассмотрим таблицу перевозок размера m·n. В ней m строк и n столбцов, всего mn клеток. Каждой клетке соответствует своя неизвестная перевозка ( i=1, 2,…, m; j=1, 2,…,n). Предположим, что мы вписали некоторое допустимое базисное решение в клетки таблицы. Клетки, соответствующие свободным переменным, как и прежде, будем называть свободными, а клетки, соответствующие базисным переменным, – базисными. Для построения следующего допустимого базисного решения введем , следуя [9], понятие цикла в таблице.

Определение. Циклом в таблице назовем замкнутую ломаную с вершинами в клетках таблицы и звеньями, параллельными строкам и столбцам, причем из каждой вершины ломаной выходят два звена, одно из них параллельно строке, другое – столбцу.

Две вершины цикла называются соседними, если являются концами одного звена. Из определения следует, что никакие три последовательные вершины цикла не лежат в одной строке или столбце. Циклом может быть самопересекающаяся ломаная, но точки самопересечения не могут быть вершинами цикла.

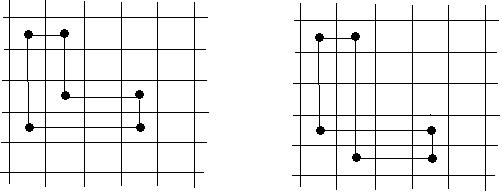
Лемма 1. Пусть в таблице из m строк и n столбцов произвольно отмечено m + n клеток (m×n ³ m + n). Тогда существует цикл, вершины которого лежат в отмеченных клетках (быть может, не во всех).

Доказательство проводится методом математической индукции по числу m + n.

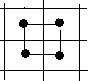
Неравенство m×n ³ m + n выполняется, только если m + n ³ 4. Если m + n = 4, то из неравенства m×n ³ m + n следует ,что m = n = 2. В этом случае существование цикла очевидно:

Предположим теперь, что лемма выполняется для всех таблиц, у которых сумма числа строк и столбцов меньше, чем m + n > 4, и докажем, что она выполняется и для таблиц с m строками и n столбцами. Возможны 2 случая:

1. В некоторой строке или в некотором столбце таблицы находится только одна отмеченная клетка. Удалим эту строку или этот столбец. Получим таблицу, у которой число отмеченных клеток равно m + n – 1 и сумма числа строк и столбцов таблицы равна m + n – 1. По индуктивному предположению для этой таблицы лемма выполняется, значит, она выполняется и для первоначальной матрицы.

2. Для каждой отмеченной клетки в ее строке и столбце имеются другие отмеченные клетки. В этом случае, начав с любой отмеченной клетки, можно, двигаясь по строке, перейти в соседнюю отмеченную клетку. От нее, двигаясь по столбцу, можно перейти к третьей отмеченной клетке и т д. Так как столбцов и строк в таблице конечное число, равное m + n, то после нескольких шагов мы попадем на строку или столбец, где уже были. В построенной ломаной будет содержаться цикл, быть может, не проходящий через все клетки.

Лемма 2. Число вершин в каждом цикле четно.

Доказательство. Рассмотрим в таблице произвольный цикл и выберем для него направление обхода, начиная с некоторой его вершины. При этом обходе в каждой вершине направление вектора – звена меняется на угол . После полного обхода цикланаправление вектора–звена совпадает с начальным. Поэтому суммарный угол поворота вектора–звена кратен . Обозначим через k количество вершин, в которых поворот звена равен , и через t – на угол . Получаем равенство: +t×(– ) = ×n, откуда следует, что k – t = 4×n или k – t + 2×t =k + t = 4×n + 2×t, т.е. число вершин цикла k + t –четное число.

Зададим в матрице произвольный цикл. Припишем каждой вершине знак плюс или минус по следующему правилу: начнем с любой вершины, припишем ей знак плюс, затем, обходя цикл в каком-либо направлении, приписываем вершинам поочередно знаки плюс и минус. Цикл с указанной расстановкой знаков назовем означеннымциклом.

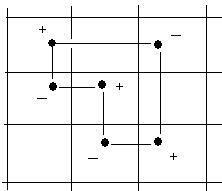
Лемма 3. В каждой строке (и столбце) матрицы число положительных вершин означенного цикла равно числу отрицательных вершин.

Доказательство. По способу расстановки знаков любая вершина цикла и соседняя с ней в строке имеют разные знаки. Следовательно, каждой положительной вершине цикла соответствует единственная отрицательная соседняя с ней в той же строке вершина цикла и наоборот, каждой отрицательной вершине цикла соответствует единственная положительная соседняя с ней в той же строке вершина цикла. Поэтому число положительных вершин цикла в любой строке равно числу отрицательных вершин в той же строке.

Пусть в клетках матрицы перевозок записано некоторое решение транспортной задачи и в ней построен означенный цикл. Увеличим все значения , стоящие в положительных клетках цикла, на число t , и уменьшим все значения , стоящие в отрицательных клетках цикла, на это же число t. Значения переменных в остальных клетках матрицы не меняем. Эту операцию назовем сдвигом по циклу на число t.

Теорема 1 (теорема о сдвиге по циклу). Сдвиг по любому означенному циклу в матрице перевозок на любое число t ¹ 0 преобразует решение системы ограничений транспортной задачи в другое решение этой системы.

Доказательство. Возьмем, например, первое уравнение системы ограничений задачи:

(1)

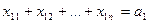
Предположим, что набор чисел является решением системы ограничений. Тогда уравнение (1) является числовым тождеством. Выберем произвольный означенный цикл в таблице перевозок. При сдвиге на t число, стоящее в любой его положительной клетке, увеличивается, а в отрицательной – уменьшается на t. Количество положительных и отрицательных вершин цикла в первой строке (и в любой другой) одинаково (лемма 3). Поэтому сумма всех элементов первой строки таблицы не изменится, а значит, уравнение (1) по-прежнему удовлетворяется. Аналогичные рассуждения справедливы для любого уравнения системы ограничений задачи. Этим теорема доказана.

Лемма 4. Каков бы ни был набор свободных переменных системы ограничений транспортной задачи, в таблице перевозок не существует цикла, все вершины которого находятся в базисных клетках.

Доказательство. Дадим свободным переменным некоторые определенные числовые значения, тогда базисные переменные также примут определенные числовые значения. Предположим теперь, что лемма 4 не выполняется. Тогда существует цикл, все вершины которого находятся в базисных клетках. Выполним сдвиг по этому циклу на некоторое число t ¹ 0. По теореме 1, мы снова получим решение системы ограничений задачи. При этом сдвиге меняются значения только базисных переменных, так как цикл проходит только через базисные клетки, а значения свободных переменных не меняются. Однако это невозможно, так как каждому набору значений свободных переменных соответствует только одно решение системы уравнений.

Определение. Циклом пересчета данной свободной клетки называется цикл, одна из вершин которого находится в данной свободной клетке, а все остальные вершины находятся в базисных клетках.

Теорема 2. В таблице перевозок для каждой свободной клетки существует, и притом единственный, цикл пересчета.

Доказательство. Возьмем произвольную свободную клетку и вместе с ней рассмотрим все m+n-1 базисных клеток этой таблицы. Вместе со свободной клеткой мы получили m + n клеток. По лемме 1 найдется цикл, все вершины которого находятся в выделенных нами клетках. Среди них будет по лемме 4 свободная клетка . Единственность такого цикла доказывается от противного, аналогично доказательству леммы 4 .

Теоремы 1 и 2 позволяют перейти от одного допустимого базисного решения транспортной задачи к другому допустимому базисному решению. Покажем, как это можно сделать на примере задачи размера 3×4:

Пункты   Станции					Запасы
	6 –	5 +
	+	– 25
Потребности

В верхнем углу каждой клетки таблицы указаны стоимости , в нижнем углу базисных клеток – числа, образующие вместе с нулевыми значениями свободных клеток допустимое базисное решение 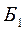задачи, построенное методом северо-западного угла:

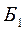= (20, 5, 0, 0, 0, 25, 20, 0, 0, 0, 25, 25);

Общая стоимость перевозок S( 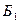)=6*20+5*5+8*25+2*20+3*25+4*25 = 560;

Возьмем свободную клетку 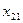и введем ее в число базисных переменных, для чего построим для нее цикл пересчета и выполним сдвиг по циклу на число t = 20 –минимальное из чисел в отрицательных клетках цикла. При этом сдвиге базисная переменная 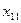получит значение ноль и, таким образом, переходит в свободные, = 5 + t = 25, = 25 – t = 5, 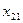= 20. В силу условия выбора значения сдвига t, новые значения переменных останутся неотрицательными, и мы получаем новое допустимое базисное решение:

Пункты   Станции					Запасы
Потребности

Новое базисное решение: =(0, 25, 0, 0, 20, 5, 20, 0, 0, 0, 25, 25);

Стоимость всех перевозок, соответствующая решению :

S( ) = 5*25+1*20+8*5+2*20+3*25+4*25 =400