Решение несбалансированной транспортной задачи
Рассмотрим транспортную задачу в которой не выполняется условие
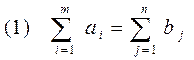
Пусть, например, вместо (1) выполняется условие
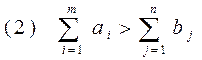
Это означает, что общие запасы груза на станциях превышают общие потребности пунктов назначения. Решая задачу составления плана перевозки, при котором потребности в грузе во всех пунктах назначения будут удовлетворены и стоимость перевозок будет минимальна, вывезти весь груз со станций не удастся. Можно преобразовать задачу в сбалансированную, если « лишний груз» t, вычисляемый по формуле:

перевезти в фиктивный пункт потребления с потребностью  , считая тарифы перевозок в этот пункт со всех станций равными нулю. Решение исходной задачи можно получить из решения полученной сбалансированной задачи с той же стоимостью перевозок, если грузы, предназначенные для перевозки в фиктивный пункт, оставить на соответствующих станциях.
, считая тарифы перевозок в этот пункт со всех станций равными нулю. Решение исходной задачи можно получить из решения полученной сбалансированной задачи с той же стоимостью перевозок, если грузы, предназначенные для перевозки в фиктивный пункт, оставить на соответствующих станциях.
Аналогично, ели выполняется условие :
 ,
,
означающее, что общие потребности груза в пунктах назначения превышают общие запасы груза на станциях, то, чтобы сбалансировать задачу, нужно ввести фиктивную станцию с недостающим запасом груза:

и нулевыми тарифами перевозок груза с этой станции во все пункты назначения. Решение исходной задачи можно получить из решения полученной сбалансированной задачи с той же стоимостью перевозок, если грузы, предназначенные для перевозки из фиктивной станции, считать «пропавшими» для соответствующих пунктов. Эти пункты не будут удовлетворены в полном объеме своих потребностей.
Пример. Найти решение транспортной задачи, исходные данные которой приведены в таблице перевозок:
| Пункты станции | Тарифы перевозок | Запасы | ||
| Потреб. |
Решение. Задача не является сбалансированной, так как
 .
.
Добавим фиктивную третью станцию с запасом груза  и с нулевыми тарифами перевозки груза, получим сбалансированную задачу с таблицей перевозок:
и с нулевыми тарифами перевозки груза, получим сбалансированную задачу с таблицей перевозок:
| Пункты станции | Тарифы перевозок | Запасы | ||
| Потреб. |
Решение этой задачи имеет вид:
 = (0, 30, 30, 40, 0, 0, 10, 0, 0), общая стоимость перевозок равна
= (0, 30, 30, 40, 0, 0, 10, 0, 0), общая стоимость перевозок равна 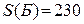 .
.
Из этого решения получаем решение исходной задачи:
 = (0, 30, 30, 40, 0, 0), с той же общей стоимостью перевозок. Однако объем перевозок в первый пункт равен лишь 40 единицам.
= (0, 30, 30, 40, 0, 0), с той же общей стоимостью перевозок. Однако объем перевозок в первый пункт равен лишь 40 единицам.
Вопросы и упражнения
1. Для транспортной задачи, условия которой заданы следующей таблицей перевозок, составить математическую модель, найти ранг системы ограничений задачи и начальное базисное решение двумя способами:
| Станции | Пункты назначения | Запасы груза гггргггруза | ||
| Потребности |
2. Найти решение транспортной задачи, исходные данные которой приведены в таблице перевозок:
| Станции | Пункты назначения | Запасы | ||||
| Потреб. |
3. Найти решение несбалансированной транспортной задачи, исходные данные которой приведены в таблице перевозок:
| Станции | Пункты назначения | Запасы | ||
| Потребности |
Дата добавления: 2016-04-14; просмотров: 876;
