Решение транспортной задачи методом потенциалов

Метод потенциалов решения транспортной задачи был разработан российским ученым, академиком Л.В. Канторовичем. Его идея аналогична симплекс–методу. Сначала строится допустимое базисное решение (например, методом северо–западного угла), затем оно последовательно улучшается с помощью цикла пересчета подходящей свободной клетки в таблице перевозок.

После построения начального допустимого базисного решения множество всех переменных системы уравнений можно разбить на два подмножества: 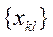– множество базисных переменных и 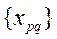–множество свободных переменных. Для анализа построенного базисного решения на оптимальность, нужно выразить функцию S –суммарную стоимость всех перевозок через свободные переменные:

(1) S =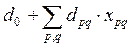

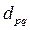Здесь свободный член равен стоимости всех перевозок построенного базисного решения. Очевидно, базисное решение будет оптимальным, если все коэффициенты при свободных переменных будут неотрицательными – в этом случае min S = 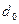достигается при нулевых значениях свободных переменных.

Критерий оптимальности базисного решения: базисное решение оптимально тогда и только тогда, когда в выражении (1) функции S через свободные переменные все коэффициенты при свободных переменных ³ 0.

Л.В. Канторович указал способ вычисления коэффициентов . Для этого он связал с каждой станцией отправления 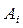новую переменную 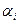(потенциал станции), а с каждым пунктом потребления – другую новую переменную 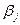(потенциал пункта). Если задача имеет размеры m×n, то получается m + n неизвестных потенциалов Для вычисления потенциалов составляется система уравнений (2):

(2)

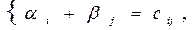
где тариф соответствующей базисной клетки. Таким образом, в системе (2) m + n – 1 уравнений (число базисных клеток) и m + n неизвестных потенциалов 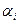и 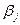. Используя теорию двойственности, можно доказать, что ранг системы (2) совпадает с рангом системы ограничений транспортной задачи, т.е. равен m + n – 1.

Поэтому одна из переменных 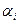или 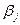является свободной (например, ), ее значение можно выбрать произвольно, значения остальных потенциалов находятся из уравнений системы (2).

Теорема Канторовича: коэффициент , с которым свободная переменная 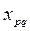входит в выражение (1) функции S через свободные переменные, вычисляется по формуле (3):

(3) =

Доказательство теоремы можно найти в [9].

Алгоритм метода потенциалов решения сбалансированной задачи :

1. Составляем математическую модель транспортной задачи.

2. Находим начальное базисное решение методом северо–западного угла или методом наименьшей стоимости. Вычисляем соответствующую стоимость всех перевозок .

3. Вычисляем потенциалы 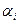и 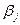, составляя систему (2). Считаем один из потенциалов, например, =0, остальные находим из системы (2).

4. Проверяем текущее базисное решение на оптимальность, для чего вычисляем коэффициенты по формуле (3). Если все ³ 0, то текущее базисное решение является оптимальным. Задача решена. В противном случае выполняем следующий шаг алгоритма.

5. Выбираем свободную клетку (p,q), для которой < 0 и строим для нее цикл пересчета.

6. Организуем сдвиг по циклу пересчета свободной клетки, находим новое базисное решение и новую суммарную стоимость перевозок по формуле (4), которая следует из формулы (1):

(4) S = 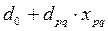, переходим к шагу 3.

Пример. Найти оптимальное решение транспортной задачи, исходные данные которой приведены в таблице перевозок:

Пункты   Станции	Тарифы перевозки груза в пункты потребления	Запасы груза на станциях
Потребности

1. Составим математическую модель задачи.

Среди неотрицательных решений системы уравнений

найти такое, при котором функция S принимает минимальное значение:

S =

2. В качестве начального базисного решения возьмем найденное ранее базисное решение, построенное методом минимальной стоимости:

Пункты   Станции	Тарифы и перевозки	Запасы груза на станциях
Потребности пунктов

В качестве начального базисного решения получаем систему чисел

= (70, 0, 30, 0, 0, 0, 10, 70, 0, 40, 20, 0)

Стоимость всех перевозок при этом решении:

S( 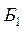) = = 970 =

3. Находим потенциалы станций и пунктов, для чего составляем систему уравнений с потенциалами для базисных клеток :

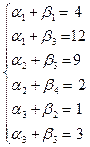Пусть 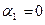. Из первого уравнения находим .

Из второго уравнения вычислим .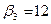

Из третьего уравнения вычислим .

Из четвертого уравнения вычислим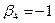

Из шестого уравнения вычислим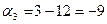

Из пятого уравнения вычислим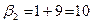

4. Проверяем решение 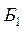на оптимальность, для чего находим коэффициенты 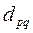в выражении S через свободные переменные.

7 – (0 + 10) = –3. Так как < 0, то базисное решение 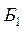не является оптимальным, переходим к следующему шагу.

5. Строим цикл пересчета для свободной клетки (1,2)

6. Выполним сдвиг по циклу пересчета свободной клетки (1,2) на величину t = min(30, 40) =30. Получим новые значения величин 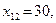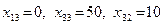. Получаем новое базисное решение:

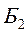= (70, 30, 0, 0, 0,0, 10, 70, 0, 10, 50, 0)

Новая стоимость всех перевозок равна: S 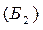= = 970 – 3×30 =880. Переменная становится базисной, а переменная 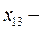свободной.

Далее возвращаемся на шаг 3. Вычисляем снова потенциалы 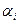и 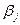, проверяем решение 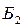на оптимальность. Теперь, легко проверить, все коэффициенты при свободных переменных в выражении S будут неотрицательными. Значит, – оптимальное решение транспортной задачи, и min S = 880.

Для решения транспортной задачи можно применить систему компьютерной алгебры Maple, так как она содержит модуль simplex, позволяющий решить любую задачу линейного программирования, в частности транспортную задачу, симплекс–методом. После загрузки Maple подключим модуль simplex, зададим систему ограничений задачи под именем sn, определим функцию стоимости всех перевозок f и найдем оптимальное решение задачи линейного программирования с помощью стандартной функции mininmize:

>with(simplex);

>сn:={x11+x12+x13+x14=100, x21+x22+x23+x24=80, x31+x32+x33+x34=60,

x11+x21+x31=70, x12+x22+x32=40, x13+x23+x33=60, x14+x24+x34=70};

>f:=4*x11+7*x12+12*x13+3*x14+5*x21+7*x22+9*x23+2*x24+6*x31+

x32+3*x33+9*x34;

> minimize(f, cn, NONNEGATIVE);

Maple выводит решение, располагая значения перевозок в произвольном порядке:

{x31 = 0, x13 = 0, x14 = 0, x21 = 0, x34 = 0, x22 = 0, x11 = 70, x23 = 10,

x24 = 70, x32 = 10, x12 = 30, x33 = 50}

Ниже приводится программа решения транспортной задачи методом потенциалов. Предполагается, что размеры m и n задачи не превышают 20, и все данные – целые числа. Информация о задаче хранится в текстовом файле ‘trans.txt’. В его первой строке записаны 2 целых числа – размеры m и n. Во второй строке записаны m чисел – запасы груза на станциях. В третьей строке записаны n чисел – потребности пунктов. Далее в m строках по n чисел в каждой строке располагаются тарифы перевозки единицы груза со станции i в соответствующий пункт j. Для рассмотренной выше задачи файл ‘transt.txt’ имеет вид:

3 4

100 80 60

70 40 60 70

4 7 12 3

5 7 9 2

6 1 3 9

Сначала программа проверяет сбалансированность задачи и выводит сообщение, если она не сбалансирована. В противном случае программа приступает к решению задачи. Процедура readf считывает данные из файла, и выводит эти данные на экран. Процедура print выводит на экран результаты – оптимальный план перевозок и его стоимость. Процедура nordwest находит начальное базисное решение методом северо–западного угла.

program transport;

uses crt;

const mm=20; mn=20; {макс. кол. поставщиков и потребителей}

qq=40; bb=10000;

var t,m,n,i,j,k,h,r,v,w,xx,yy:integer;

x,z:array[1..mm,1..mn] of integer; {решение и тарифы}

a:array[1..mm] of integer; {поставки}

b:array[1..mn] of integer; {потребности}

e,g:array[1..qq] of integer; {массивы индексов базисных клеток}

p:boolean; f:text;

procedure readf;

begin assign(f,'trans.txt'); reset(f);

writeln('ТРАНСПОРТНАЯ ЗАДАЧА':50);

readln(f,m,n);

writeln('кол. станций: ',m);

writeln('кол. пунктов потребления: ',n);

writeln('запасы груза на станциях:');

for i:=1 to m do

begin read(f,a[i]); write(a[i]:4);

end; writeln;

writeln('потребности пунктов:');

for i:=1 to n do

begin read(f,b[i]); write(b[i]:4);

end; writeln;

writeln('таблица тарифов перевозок: ');

for i:=1 to m do

begin for j:=1 to n do

begin read(f,z[i,j]); write(z[i,j]:4)

end; writeln;

end; close(f);

end;

procedure nordwest;

begin i:=1; j:=1;

for h:=1 to n+m-1 do

begin r:=a[i]-b[j];

if (r>0) or ((r=0) and (b[j]<>0)) then

begin w:=b[j];

if w<>0 then x[i,j]:=w else x[i,j]:=-1;

e[h]:=i; g[h]:=j;

a[i]:=r; b[j]:=0;

if j<n then j:=j+1

end else

begin w:=a[i];

if w<>0 then x[i,j]:=w else x[i,j]:=-1;

e[h]:=i; g[h]:=j;

a[i]:=0; b[j]:=-r;

if i<m then i:=i+1

end

end;

end;

procedure print;

var F:integer;

begin F:=0; writeln;

writeln(' оптимальный план перевозок: ':30); writeln;

writeln('станция':10,'пункт ':12,'количество':12);

for i:=1 to 40 do write('-'); writeln;

for i:=1 to m do

for j:=1 to n do

if x[i,j]>0 then

begin F:=F+x[i,j]*z[i,j];

writeln(i:10,j:10,x[i,j]:10)

end; writeln;

writeln('min F=':25,F)

end;

procedure potencials; {здесь a и b-массивы потенциалов пунктов}

begin t:=bb; {xx,yy-координаты своб. клетки}

for i:=1 to m do a[i]:=t; for j:=1 to n do b[j]:=t;

a[1]:=0;

repeat r:=0;

for h:=1 to m+n-1 do

begin i:=e[h]; j:=g[h];

if x[i,j]<>0 then

begin xx:=a[i]; yy:=b[j];

if (xx=bb) and (yy<>bb) then

begin a[i]:=z[i,j]-yy;

r:=1

end else

if (xx<>bb) and (yy=bb) then

begin b[j]:=z[i,j]-xx;

r:=1

end

end

end

until r=0;

end;

function proverka:boolean;

begin p:=true; r:=0;

for i:=1 to m do

for j:=1 to n do

begin t:=a[i]+b[j]-z[i,j];

if t>r then

begin p:=false; xx:=i;

yy:=j; r:=t

end

end; proverka:=p

end;

procedure cancel; {здесь a и b-кол. баз. клеток в строках и столбцах}

begin t:=0;

for i:=1 to m do a[i]:=t; for j:=1 to n do b[j]:=t;

for i:=1 to m do for j:=1 to n do

if x[i,j]<>0 then

begin a[i]:=a[i]+1;

b[j]:=b[j]+1

end;

repeat r:=0;

for i:=1 to m do

if (a[i]<>-1) and (a[i]<=1) and (i<>xx) then

begin a[i]:=-1; r:=1;

for j:=1 to n do

if (b[j]<>-1) and (x[i,j]<>0) then

begin b[j]:=b[j]-1;

if b[j]=0 then b[j]:=-1

end

end;

for j:=1 to n do

if (b[j]<>-1) and (b[j]<=1) and (j<>yy) then

begin b[j]:=-1; r:=1;

for i:=1 to m do

if (a[i]<>-1) and (x[i,j]<>0) then

begin a[i]:=a[i]-1;

if a[i]=0 then a[i]:=-1

end

end

until r=0

end;

procedure zikl;

procedure vert;

begin k:=i; i:=1;

while (a[i]=-1) or (i=k) or (x[i,j]=0) do i:=i+1;

r:=x[i,j];

if w>r then w:=r;

end;

begin i:=xx; j:=yy; w:=bb;

vert;

while i<>xx do

begin k:=j; j:=1;

while (b[j]=-1) or (j=k) or (x[i,j]=0) do j:=j+1;

vert;

end;

end;

procedure mo;

begin h:=1;

while h<=n+m-1 do

begin if (e[h]=i) and (g[h]=j) then

begin e[h]:=xx; g[h]:=yy;

h:=m+n

end else h:=h+1

end

end;

procedure move;

label 1;

procedure vert1;

begin k:=i; i:=1;

while (a[i]=-1) or (i=k) or (x[i,j]=0) do i:=i+1

end;

begin i:=xx; j:=yy; v:=0;

if w=-1 then w:=0;

vert1;

1:r:=x[i,j];

if r<0 then

begin mo; x[i,j]:=0; x[xx,yy]:=-1

end {выход}

else

begin if r<=w then

if v<>0 then x[i,j]:=-1 else

begin mo; x[i,j]:=0; v:=1

end

else x[i,j]:=r-w;

if i=xx then x[xx,yy]:=w {выход}

else

begin k:=j; j:=1;

while (b[j]=-1) or (j=k) or (x[i,j]=0) do j:=j+1;

if x[i,j]>0 then

begin x[i,j]:=x[i,j]+w;

vert1; goto 1

end else

if w>0 then

begin x[i,j]:=w;

vert1

end; goto 1

end

end

end;

begin clrscr;

readf; t:=0; v:=0;

for i:=1 to m do t:=t+a[i];

for j:=1 to n do v:=v+b[j];

if t<>v then writeln('задача не сбалансирована':30) else

begin for i:=1 to m do

for j:=1 to n do x[i,j]:=0;

nordwest; potencials;

while proverka=false do

begin cancel;

zikl;

move;

potencials

end; print

end; readkey;

end.