Задача минимизации расходов

Нелинейное программирование

Задачи оптимизации, в которых целевая функция не является линейной функцией своих аргументов или среди условий, определяющих их допустимые значения, могут быть нелинейные уравнения и неравенства, называются задачами нелинейного программирования. Нелинейное программирование широко применяется в экономике при управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и послужило основой широкого использования математических методов в экономике. В качестве примеров рассмотрим две простейших задачи нелинейного программирования: задачу минимизации расходов при реализации продукции и задачу максимизации объема производства.

Задача минимизации расходов

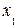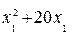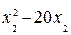Фирма реализует автомобили двумя способами: через розничную торговлю и оптом. При реализации автомобилей в розницу расходы на реализацию составляют условных единиц, а при продаже автомобилей оптом – таких же единиц. Найти оптимальный способ реализации 100 автомобилей, минимизирующий суммарные расходы.

Математическая модель задачи заключается в следующем:

Найти неотрицательное решение уравнения

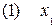+ =100 (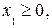

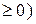
при котором функция

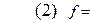
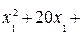
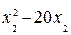принимает минимальное значение.

Так как целевая функция не является линейной, то эта задача является задачей нелинейного программирования. Найдем ее решение, используя геометрическую интерпретацию.

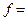
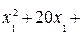
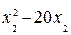
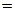
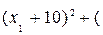
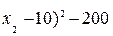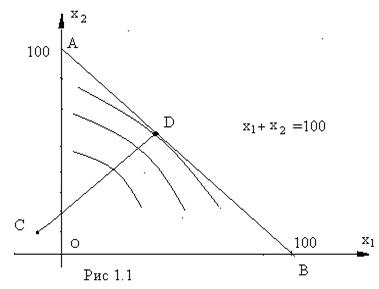
Так как , то линиями уровня функции 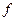являются окружности разных радиусов с центром в точке C(-10, 10), а областью допустимых решений задачи – отрезок AB прямой 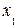+ =100 (рис. 1.1).

Если проводить эти окружности из точки C, то нетрудно догадаться, что минимальное значение функция 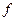принимает в точке D касания окружности уровня с отрезком AB. Радиус этой окружности будет перпендикулярен прямой AB, поэтому угловой коэффициент k прямой CD равен единице: k=1. Следовательно, уравнение прямой CD имеет вид:

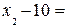
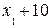, или 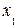– 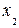= –20.

Решая систему уравнений

,

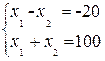находим координаты точки D: 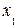= 40, 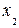= 60. Значит , фирма должна продать в розницу 40 автомобилей, а оптом – 60 автомобилей, при этом суммарные расходы составят 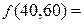1600 + 800 + 3600 – 1200 = 4800 условных единиц.