Метод множителей Лагранжа
|
|

Метод Лагранжа─ это метод решения задачи условной оптимизации, при котором ограничения, записываемые как неявные функции, объединяются с целевой функцией в форме нового уравнения, называемого лагранжианом.
Рассмотрим частный случай общей задачи нелинейного программирования:
Дана система нелинейных уравнений (1):
(1) gi(x1,x2,…,xn)=bi (i=1..m),
Найти наименьшее (или наибольшее) значение функции (2)
(2) f (х1,х2,…,хn ),
если отсутствуют условия неотрицательности переменных и f(х1,х2,…,хn ) и gi(x1,x2,…,xn) ─ функции, непрерывные вместе со своими частными производными.
Чтобы найти решение этой задачи, можно применить следующий метод: 1. Вводят набор переменных λ1, λ2,…, λm, называемых множителями Лагранжа, составляют функцию Лагранжа (3)
(3) F(х1,х2,…,хn , λ1,λ2,…,λm) = f(х1,х2,…,хn )+ 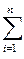 λi [bi-gi (x1,x2,…,xn)].
λi [bi-gi (x1,x2,…,xn)].
2. Находят частные производные от функции Лагранжа по переменным xi и λi и приравнивают их нулю.
3. Решая систему уравнений, находят точки, в которых целевая функция задачи может иметь экстремум.
4.Среди точек, подозрительных не экстремум, находят такие, в которыхдостигается экстремум, и вычисляют значения функции в этих точках.
4. Сравнить полученные значения функции f и выбрать наилучшее.
Задача:
По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. При производстве х1 изделия I способом затраты равны 4*х1+х1^2 руб., а при изготовлении х2 изделий II способом они составляют 8*х2+х2^2 руб. Определить, сколько изделий каждым из способов следует изготовить, так чтобы общие затраты на производство продукции были минимальными.
Решение: Математическая постановка задачи состоит в определении наименьшего значения функции двух переменных:
f = 4*x1+x1^2 +8*x2 +x2^2, при условии x1 +x2 = 180.
Составим функцию Лагранжа:
F(x1,x2,λ) = 4*x1+x1^2+8*x2+x2^2+λ*(180-x1-x2).
Вычислим ее частные производные по х1,х2, λ и приравняем их к 0:
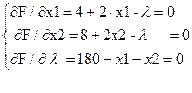
Перенесем в правые части первых двух уравнений λ и приравняем их левые части, получим 4 + 2*x1 = 8 + 2*x2, или x1 − x2 = 2.
Решая последнее уравнение совместно с уравнением x1 + x2 = 180, находим x1 = 91, x2 = 89, то есть получили решение, удовлетворяющее условиям:
x1, x2 ≥ 0.
Найдем значение целевой функции f при этих значениях переменных:
F(x1, x2) = 17278
Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке (91,89) функция f имеет минимум.
Можно сравнить это значение со значением f в соседних точках:
f(90,90) = 17280 >17278 =f(91,89).
Для решения системы линейных уравнений можно использовать пакет Maple, в котором есть процедура solve(s, {mn}), где s − имя системы уравнений, mn − множество имен переменных:
> s:={4+2*x1-L=0, 8+2*x2-L=0, 180-x1-x2=0};
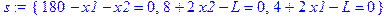
> solve(s,{x1,x2,L});
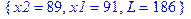
Дата добавления: 2016-04-14; просмотров: 2121;
