Графический метод решения задачи нелинейного программирования
В общем виде задача нелинейного программирования (ЗНП) формулируется следующим образом: найти решение X*= 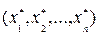 системы ограничений
системы ограничений
 (6)
(6) 
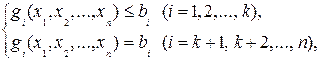
при котором целевая функция
(7) 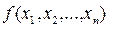

принимает наибольшее (или наименьшее) значение. Предполагается , что хотя бы одна из функций в (6) или в (7) не линейна.
Для ЗНП в отличие от ЗЛП нет единого метода решения. В зависимости от вида целевой функции (7) и системы ограничений (6) разработаны специальные методы решения, например, метод множителей Лагранжа для ЗНП с системой ограничений, состоящей только из уравнений, и при условии, что все функции в (6) и (7) имеют непрерывные частные производные.
В ЗНП разыскивается наибольшее или наименьшее значение целевой функции – ее глобальный максимум или глобальный минимум. Однако целевая функция может иметь локальные экстремумы, что затрудняет решение ЗНП, так как большинство существующих методов нелинейного программирования не позволяет установить, является ли найденный экстремум локальным или глобальным.
ЗНП с двумя переменными может быть решена графически, как было показано в предыдущих разделах. Графическое решение задачи может быть разбито на следующие части:
1. В прямоугольной системе координат 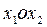 определяется область решений системы (6).
определяется область решений системы (6).
2. Определяется тип линий уровня целевой функции 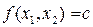 .
.
3. Находится линия уровня целевой функции с наибольшим (или наименьшим) значением уровня или устанавливается неразрешимость задачи из-за неограниченности функции на множестве решений системы (6).
4. Определяются координаты точки области решений системы (6), через которую проходит линия уровня, найденная в пункте 3.
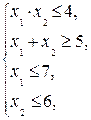
Пример. Найти неотрицательное решение системы неравенств
(8) 
при котором функция 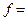
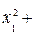
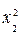 имеет наибольшее значение.
имеет наибольшее значение.
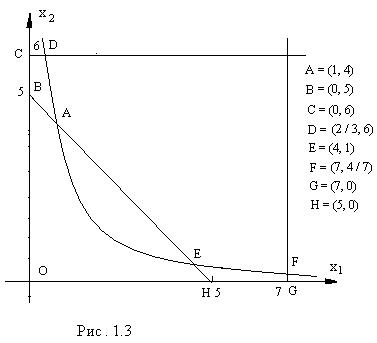
Решение. Область неотрицательных решений системы (8) состоит из двух частей – криволинейных четырехугольников ABCD и EFGH (рис. 1.3), ограниченных осями координат, прямыми 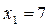 ,
, 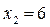 и
и 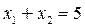 и гиперболой
и гиперболой 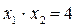
Линиями уровня функции 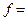
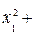
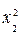 = c являются окружности с центром в начале координат O(0, 0). Окружность наибольшего радиуса, имеющая общие точки с областью решений системы (8), пройдет либо через точку D, либо через точку F, так как эти точки наиболее удалены от начала координат. Найдем координаты точек D и F, решая системы
= c являются окружности с центром в начале координат O(0, 0). Окружность наибольшего радиуса, имеющая общие точки с областью решений системы (8), пройдет либо через точку D, либо через точку F, так как эти точки наиболее удалены от начала координат. Найдем координаты точек D и F, решая системы
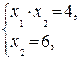
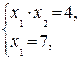
и получим, что D = (2/3, 6) и F = (7, 4/7).
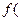 D) = 36
D) = 36 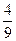 ,
, 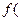 F) =49
F) =49 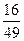 ,
,
следовательно, max 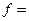
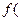 F) = 49
F) = 49 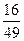 ,
, 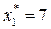 ,
, 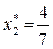 .
.
Дата добавления: 2016-04-14; просмотров: 5394;
