Известно, для любого момента времени для электрической цепи, содержащей и , дифференциальное уравнение равновесия падений напряжений для любой фазы, например, для фазы , имеет вид
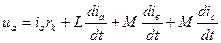 , (3.1)
, (3.1)
где 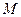 -коэффициент взаимоиндукции между фазами.
-коэффициент взаимоиндукции между фазами.
Имея в виду, что в трехфазной сети с изолированной нейтралью в любой момент времени имеет место соотношение 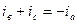 , можно это уравнение представить (опуская индекс фазы)
, можно это уравнение представить (опуская индекс фазы)
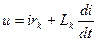 , (3.2)
, (3.2)
где 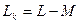 - результирующая индуктивность фазы, то есть индуктивность с учетом влияния двух других фаз.
- результирующая индуктивность фазы, то есть индуктивность с учетом влияния двух других фаз.
Решение (3.2), например, для фазы  , имеет вид (для дифференциального уравнения первого порядка с правой частью, отличной от нуля)
, имеет вид (для дифференциального уравнения первого порядка с правой частью, отличной от нуля)
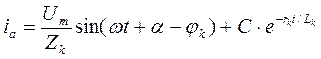 , (3.3)
, (3.3)
где 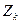 - полное сопротивление присоединенного к источнику участка цепи или цепи к.з.;
- полное сопротивление присоединенного к источнику участка цепи или цепи к.з.; 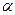 - угол, определяющий значение проекции
- угол, определяющий значение проекции 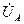 на ось времени
на ось времени 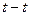 в момент времени
в момент времени 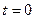 (иначе, фаза включения);
(иначе, фаза включения);
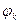 - угол сдвига тока фазы по отношению к напряжению фазы в цепи к.з.;
- угол сдвига тока фазы по отношению к напряжению фазы в цепи к.з.;
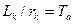 - постоянная времени цепи к.з.
- постоянная времени цепи к.з.
Первый член правой части (3.3) представляет собой синусоиду (периодическую слагающую полного тока 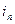 , которая при рассматриваемых условиях является принужденным током с постоянной амплитудой
, которая при рассматриваемых условиях является принужденным током с постоянной амплитудой 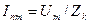 . Соответственно, второй член решения представляет собой затухающий по закону экспоненты свободный ток
. Соответственно, второй член решения представляет собой затухающий по закону экспоненты свободный ток 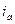 (апериодическая слагающая полного тока), начальное значение которого определяют из начальных условий, то есть
(апериодическая слагающая полного тока), начальное значение которого определяют из начальных условий, то есть 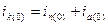 . (3.4)
. (3.4)
Согласно правилу Ленца в момент времени 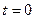 для фазы
для фазы  ,
, 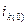 должен равняться току режима, предшествующему к.з.
должен равняться току режима, предшествующему к.з.
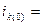
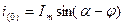 . (3.5)
. (3.5)
Подставляя выражение 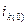 из (3.5) в (3.4), получим
из (3.5) в (3.4), получим
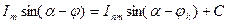 , (3.6)
, (3.6)
где 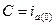 - начальное значение апериодической слагающей тока к.з.
- начальное значение апериодической слагающей тока к.з.
Следовательно, можно записать
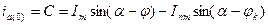 . (3.7)
. (3.7)
Переходя к обозначениям, принятым в расчетах токов к.з, можно записать, что для любой фазы 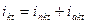 ,
,
где 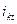 - мгновенное значение полного тока к.з.;
- мгновенное значение полного тока к.з.; 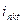 - мгновенное значение периодической слагающей полного тока к.з.;
- мгновенное значение периодической слагающей полного тока к.з.; 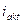 - мгновенное значение апериодической слагающей полного тока к.з.
- мгновенное значение апериодической слагающей полного тока к.з.
Подставляя значения 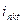 и
и 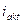 из (3.3) и (3.7), можно для фазы
из (3.3) и (3.7), можно для фазы  записать
записать
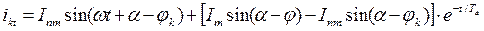 . (3.8)
. (3.8)
Выражение (3.8) определяет полный ток фазы  при трехфазном к.з. в переходном процессе (при питании короткозамкнутой цепи от источника неограниченной мощности).
при трехфазном к.з. в переходном процессе (при питании короткозамкнутой цепи от источника неограниченной мощности).
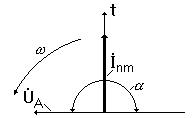
Рассматриваемый переходный процесс можно проиллюстрировать графически, если воспользоваться векторной диаграммой рис.3.2.
Из формулы (3.7) для фазы  , имеем
, имеем 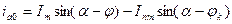 .
.
Следовательно, значение 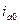 можно представить как
можно представить как 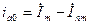 или
или
 |
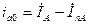 , то есть как разность векторов
, то есть как разность векторов 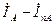 , спроектированную на ось времени
, спроектированную на ось времени 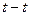 (см. рис.3.3).
(см. рис.3.3).
Рис.3.3.
Отмечая на оси 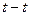 значения проекции этой разности, получаем
значения проекции этой разности, получаем 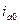 в виде отрезка
в виде отрезка 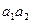 . Там же (на оси
. Там же (на оси 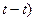 отрезки
отрезки 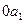 -мгновенное значение полного тока до к.з., а
-мгновенное значение полного тока до к.з., а 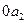 -мгновенное значение периодической слагающей тока к.з.
-мгновенное значение периодической слагающей тока к.з.
На оси 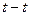 откладываем начальное значение апериодической слагающей тока к.з.
откладываем начальное значение апериодической слагающей тока к.з. 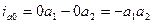 . Поэтому отрезок
. Поэтому отрезок 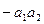 отложен вверх от точки
отложен вверх от точки 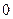 по оси
по оси 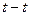 (отрезок
(отрезок 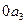 ).
).
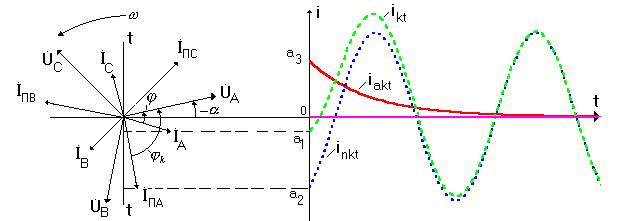
Развертывая далее переходный процесс во времени, получим осциллограмму рис.3.3.
На осциллограмме отмечены: 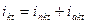 -полный ток к.з. ( для фазы
-полный ток к.з. ( для фазы  );
);
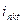 -периодическая слагающая тока к.з.;
-периодическая слагающая тока к.з.; 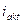 -апериодическая слагающая тока к.з.
-апериодическая слагающая тока к.з.
Аналогично можно построить осциллограммы тока к.з. для фаз 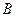 и
и 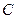 .
.
Наибольшее начальное значение апериодической слагающей тока к.з.
Как следует из осциллограммы рис.3.3. максимальное мгновенное значение полного тока к.з. фазы зависит от положения вектора ( 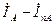 ), то есть от значения
), то есть от значения 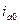 , которое может изменяться от нуля (когда вектор
, которое может изменяться от нуля (когда вектор 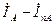 перпендикулярен оси
перпендикулярен оси 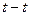 ) до
) до 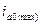 , когда вектор
, когда вектор 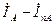 параллелен оси
параллелен оси 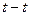 . В свою очередь, положение вектора
. В свою очередь, положение вектора 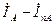 в момент возникновения к.з. зависит от фазы включения – угла
в момент возникновения к.з. зависит от фазы включения – угла 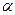 .
.
Кроме того, значение 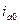 зависит также от величины тока до к.з., то есть от тока
зависит также от величины тока до к.з., то есть от тока 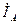 .
.
Очевидно, что если 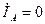 (то есть фаза
(то есть фаза  до к.з. была не нагружена (холостой ход)), то выражением для
до к.з. была не нагружена (холостой ход)), то выражением для 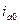 будет формула
будет формула
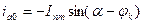 . (3.9)
. (3.9)
Таким образом, наибольшее значение 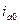 будет иметь место в том случае, если:
будет иметь место в том случае, если:
а) электрическая цепь до к.з. была ненагруженной;
б) фаза включения напряжения ( 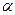 ) для рассматриваемой фазы равна
) для рассматриваемой фазы равна 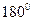 или
или 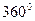 , то есть проекция вектора
, то есть проекция вектора 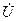 на ось
на ось 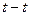 равна нулю (рис.3.4).
равна нулю (рис.3.4).
 |
В этом случае
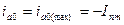 . (3.10)
. (3.10)
Рис.3.4.
Осциллограмма тока к.з. для фазы  при переходном процессе, когда
при переходном процессе, когда 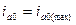 приведена на рис.3.5.
приведена на рис.3.5.
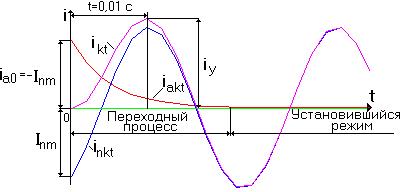 |
Рис.3.5.
На осциллограмме 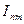 - амплитудное значение периодической слагающей тока к.з.;
- амплитудное значение периодической слагающей тока к.з.; 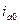 - начальное значение апериодической слагающей тока к.з. При этом
- начальное значение апериодической слагающей тока к.з. При этом 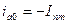 .
.
Как следует из осциллограммы, переходный процесс заканчивается к моменту исчезновения апериодической слагающей тока к.з., а 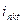 не затухает в переходном процессе и этим своим значением переходит в установившийся ток при к.з., то есть
не затухает в переходном процессе и этим своим значением переходит в установившийся ток при к.з., то есть 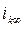 .
.
Заметим, что периодическая слагающая тока к.з. остается симметричной, тогда как апериодическая слагающая 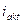 и полный ток к.з.
и полный ток к.з. 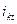 несимметричны относительно оси
несимметричны относительно оси 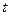 в переходном процессе. То же самое имеет место в фазах
в переходном процессе. То же самое имеет место в фазах  и
и  .
.
Асимметрия полного тока к.з. относительно оси времени обусловлена наличием апериодической слагающей тока к.з., которая является криволинейной осью симметрии полного тока к.з. . Поэтому следует иметь в виду, что понятие трехфазное к.з. является симметричным справедливо только для периодических слагающих полного тока трех фаз. Полные же токи к.з. в трех фазах будут неодинаковыми, и, разумеется, несимметричными.
Дата добавления: 2016-04-14; просмотров: 896;
