ОБ ЭЛЕКТРОМАГНИТНЫХ ПЕРЕХОДНЫХ ПРОЦЕССАХ
ОСНОВНЫЕ СВЕДЕНИЯ
2.1.1. Основные определения
Из всего многообразия электромагнитных переходных процессов в электрической сети наиболее распространенными являются процессы, обусловленные:
а) коротким замыканием в сети, а также повторным включением и отключением короткозамкнутой цепи; б) включением и отключением двигателей и других приемников электрической энергии; в) несинхронным включением синхронных машин.
К о р о т к и м з а м ы к а н и е м называют всякое не предусмотренное нормальными условиями работы замыкание между фазами, а в системах с заземленными нейтралями – также замыкание одной или несколько фаз на землю.
В системах с незаземленными нейтралями или с нейтралями, заземленными через специальные компенсирующие устройства, замыкание одной из фаз на землю называют простым замыканием. При этом виде повреждения прохождение тока обусловлено только емкостью фаз относительно земли.
При возникновении короткого замыкания (к.з.) в сети сопротивление короткозамкнутой цепи уменьшается, что приводит к увеличению токов в отдельных ветвях сети по сравнению с их значениями в нормальном режиме.
Обычно в месте к.з. образуется некоторое переходное сопротивление, состоящее из сопротивления возникшей электрической дуги и сопротивлений прочих элементов пути тока.
В ряде случаев переходные сопротивления могут быть столь малы, что практически ими можно пренебречь. Такие к.з. называют металлическими.
Очевидно, что при прочих равных условиях ток при металлическом к.з. больше, чем при наличии переходного сопротивления.
В трехфазных системах с заземленной нейтралью различают следующие основные виды к.з. в одной точке: трехфазное; двухфазное; однофазное и двухфазное на землю, то есть замыкание между двумя фазами с одновременным замыканием той же точки на землю.
Трехфазное к.з. является симметричным, так как при нем все фазы остаются в одинаковых условиях. Напротив, все остальные виды к.з. являются несимметричными, поскольку при каждом из них фазы находятся уже в неодинаковых условиях.
Аварийная статистика по электрическим системам России показывает, что при глухозаземленной нейтрали относительная вероятность различных 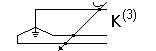 видов к.з. (в процентах) характеризуется данными:
видов к.з. (в процентах) характеризуется данными:
 Трехфазное;
Трехфазное; 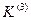 ; 5%;
; 5%;
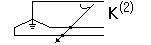
 Двухфазное;
Двухфазное; 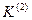 ; 10%;
; 10%;
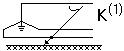
Однофазное; 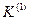 ; 65%;
; 65%;

Двухфазное на землю; 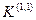 ; 20%.
; 20%.
Здесь, соответственно, показано: принципиальная схема, название вида к.з.; буквенное обозначение на схемах места и вида к.з.; относительная вероятность вида к.з., %.
Нередко в процессе развития аварии первоначальный вид к.з. переходит в другой вид к.з. Так, например, в кабельных сетях с трехжильными кабелями несимметричные к.з. часто переходят в трехфазное к.з., так как образовавшаяся при повреждении в кабеле электрическая дуга быстро разрушает изоляцию между его жилами.
Несимметричные к.з., а также несимметричные нагрузки по существу представляют различные виды поперечной несимметрии.
Нарушение симметрии какого-либо промежуточного элемента трехфазной цепи (например, обрыв одной фазы линии электропередачи) называют продольной несимметрией.
2.1.2. Причины возникновения и следствия
Основной причиной возникновения рассматриваемых в дальнейшем электромагнитных переходных процессов являются преимущественно короткие замыкания. Последние, в свою очередь, являются результатом нарушения изоляции электрического оборудования.
В зависимости от места возникновения и продолжительности повреждения его последствия могут иметь местный характер или, напротив, могут отражаться на всей сети.
Ток к.з. даже в тех случаях, когда он мал по сравнению с номинальным током генератора, обычно во много раз превышает номинальный ток самой аварийной ветви. Поэтому и при кратковременном прохождении тока к.з. он может вызвать дополнительный нагрев токоведущих элементов и проводников выше допустимого значения.
Кроме теплового действия, токи к.з. вызывают между проводниками фаз большие механические усилия. При недостаточной прочности проводников и их креплений они могут быть разрушены при к.з.
При замыканиях на землю возникают неуравновешенные системы токов, которые способны создавать магнитные потоки, достаточные для наведения в соседних линиях связи величины э.д.с., опасные для обслуживающего персонала.
Наконец, при задержке отключения к.з. сверх допустимой продолжительности может произойти нарушение устойчивой работы электрической системы.
2.1.3. Назначение расчетов и требования, предъявляемые к ним
Под расчетом электромагнитного переходного процесса обычно понимают вычисление токов и напряжений в рассматриваемой схеме при заданных исходных условиях.
К числу задач, для практического решения которых производят такие расчеты, относятся:
а) сопоставление, оценка и выбор схемы электрических соединений как отдельных установок (станций, подстанций), так и электрической системы в целом;
б) выявление условий работы потребителей при аварийных режимах;
в) выбор аппаратов и проводников и их проверка по условиям работы при к.з.;
г) проектирование и настройка устройств релейной защиты;
д) анализ происшедших аварий;
е) определение числа и места размещения в электрической системе заземленных нейтралей;
ж) подбор характеристик разрядников для защиты установок от перенапряжений (включая защиту статических конденсаторов установок продольной компенсации);
з) оценка и выбор систем возбуждения синхронных машин;
и) проектирование и проверка защитных заземлений;
к) оценка влияния линий электропередачи на линии связи и сигнализации;
л) проведение различных испытаний.
Особенностью расчетов при решении задач, встречающихся в эксплуатации, является необходимость учета конкретных условий рассматриваемого переходного процесса. При проектировании, напротив, часто довольствуются приближенными данными.
2.2. ОБЩИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАСЧЕТОВ
2.2.1. Основные допущения
Расчет электромагнитного переходного процесса в современной электрической системе с учетом всех имеющих место условий и факторов чрезвычайно сложен. Поэтому, чтобы упростить задачу и сделать ее решение практически возможным, вводят ряд допущений, которые зависят прежде всего от характера и постановки самой задачи. Следует иметь в виду, что нередко те допущения, которые пригодны для решения одной задачи, могут быть совершенно неприемлемыми при решении другой.
Рассмотрим основные допущения, которые обычно принимают при решении большинства практических задач, связанных с определением токов и напряжений при электромагнитных переходных процессах. К числу таких допущений можно отнести:
а) отсутствие насыщения магнитных систем. При этом все элементы схем обладают линейными характеристиками;
б) пренебрежение токами намагничивания силовых трансформаторов и автотрансформаторов;
в) сохранение симметрии трехфазной системы до места повреждения;
г) пренебрежение емкостными проводимостями;
д) приближенный учет нагрузок;
е) неучет активных сопротивлений при определенных условиях;
ж) отсутствие качаний роторов синхронных машин.
2.2.2. Понятие о расчетных условиях
В соответствии с целевым назначением расчета электромагнитного переходного процесса устанавливают исходные расчетные условия, которые весьма разнообразны и при решении различных задач могут быть даже противоположными.
Так, например, для выбора высоковольтного выключателя по условиям его работы при к.з. должны быть определены соответствующие возможные наибольшие величины тока к.з. С этой целью исходят из предположения, что к.з. происходит в то время, когда включено наибольшее число генераторов, что вид к.з. такой, при котором ток достигает наибольшей величины, что к.з. металлическое и что оно произошло непосредственно у выводов самого выключателя.
Для выбора трубчатого разрядника требуется знать не только наибольшую, но и возможно наименьшую величину тока к.з., для определения которой, очевидно, должны быть приняты совсем иные расчетные условия.
2.2.3. Основные понятия о системе относительных единиц
Анализ электромагнитных переходных процессов показывает, что представление любых физических величин в относительных (безразмерных) единицах позволяет существенно упростить некоторые теоретические выкладки и придать им общий характер. В практических расчетах такое представление величин придает результатам большую наглядность и позволяет лучше ориентироваться в порядке определяемых значений.
Для применения системы относительных единиц необходимо принять какую-то физическую величину за единицу измерения и, как говорят в практике расчета тока к.з., выбрать базисные условия.
Для расчета токов к.з. достаточно выбрать базисные условия для полной мощности 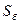 (
( 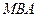 ), линейного напряжения
), линейного напряжения 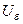 (
( 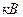 ), тока
), тока 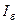 (
( 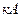 ) и сопротивления
) и сопротивления 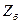 (
( 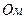 ).
).
Между значениями произвольно выбранных базисных условий существует следующая связь:
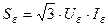 ; (2.1)
; (2.1)
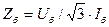 . (2.2)
. (2.2)
Из (2.1) и (2.2) следует, что если из 4-х базисных величин 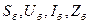 двумя из них задаться произвольно, то две другие базисные величины будут производными от них.
двумя из них задаться произвольно, то две другие базисные величины будут производными от них.
Практика расчетов токов к.з. показала, что целесообразно задаваться базисной мощностью 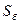 и базисным напряжением
и базисным напряжением 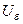 (основные базисные единицы), при этом базисный ток
(основные базисные единицы), при этом базисный ток 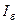 и базисное сопротивление
и базисное сопротивление 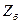 будут производными от их значений.
будут производными от их значений.
На практике в качестве 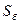 принимают значение трехфазной мощности, за базисное напряжение
принимают значение трехфазной мощности, за базисное напряжение 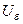 - линейное напряжение.
- линейное напряжение.
Таким образом, если выбраны значения 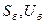 и получены производные от них
и получены производные от них 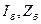 , то все величины, участвующие в расчете электромагнитного переходного процесса могут быть выражены через них в виде относительных величин.
, то все величины, участвующие в расчете электромагнитного переходного процесса могут быть выражены через них в виде относительных величин.
Так, например, для э.д.с. 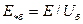 , (2.3)
, (2.3)
где 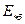 - значение э.д.с. в относительных единицах, приведенное к базисным условиям;
- значение э.д.с. в относительных единицах, приведенное к базисным условиям; 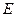 - заданное значение э.д.с. в кВ;
- заданное значение э.д.с. в кВ; 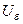 - напряжение в кВ, принятое за основную базисную единицу.
- напряжение в кВ, принятое за основную базисную единицу.
Из (2.3) следует 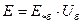 , кВ. (2.4)
, кВ. (2.4)
Таким образом, формула (2.4) служит для перехода от значения величины в относительных единицах к ее именованному значению.
Аналогично, например, выводятся следующие формулы:
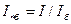 ; (2.5)
; (2.5)
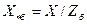 ; (2.6)
; (2.6)
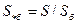 . (2.7)
. (2.7)
Если в формулу (2.2) подставить значение 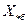 из (2.6), то получим
из (2.6), то получим
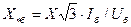 . (2.8)
. (2.8)
Формула (2.8) позволяет при заданных базисных условиях и заданном значении 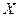 (Ом) элемента цепи определить его значение в относительных единицах, приведенное к базисным условиям.
(Ом) элемента цепи определить его значение в относительных единицах, приведенное к базисным условиям.
Если правую часть (2.8) умножить на отношение 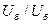 , то формула примет вид
, то формула примет вид
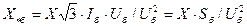 . (2.9)
. (2.9)
Ранее отмечалось, что выбор значений базисных единиц является произвольным. Следовательно, одна и та же действительная величина может иметь различное значение в относительных единицах. Чтобы исключить возможные неувязки, принято параметры элементов схемы, приводимые в справочниках, выражать в номинальных относительных единицах (то есть в качестве единиц измерения приняты значения номинальных параметров).
Исходя из сказанного, по формулам (2.8) и (2.9) имеем
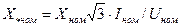 ; (2.10)
; (2.10)
 или
или 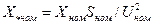 . (2.11)
. (2.11)
Формулы (2.10) и (2.11) позволяют по известному значению 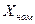 (Ом) определить
(Ом) определить 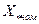 и наоборот.
и наоборот.
Далее, если из (2.10) выразить 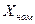 и подставить его выражение в (2.8), то получим
и подставить его выражение в (2.8), то получим 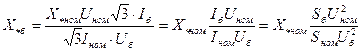 . (2.12)
. (2.12)
Формула (2.12) позволяет приводить к базисным условиям сопротивления элементов схемы, выраженные через их номинальные относительные сопротивления.
В практике расчетов токов к.з. величина базисной мощности 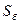 выбирается с таким условием, чтобы упростить расчет. Поэтому за
выбирается с таким условием, чтобы упростить расчет. Поэтому за 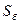 в зависимости от мощности источников, питающих сеть, принимают обычно значение 1, 10, 100 или 1000
в зависимости от мощности источников, питающих сеть, принимают обычно значение 1, 10, 100 или 1000  . За базисное напряжение принимают значение напряжение, равное среднему номинальному напряжению сети или близкое к нему, то есть
. За базисное напряжение принимают значение напряжение, равное среднему номинальному напряжению сети или близкое к нему, то есть 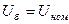 . Тогда формула (2.12) примет вид
. Тогда формула (2.12) примет вид
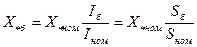 . (2.13)
. (2.13)
Примечание. Если реактор, установленный в сети, имеет номинальное напряжение выше, чем номинальное напряжение сети ( с целью получения большей величины сопротивления), в которой он установлен, то его сопротивление в относительных единицах, приведенное к базисным условиям, должно определяться по (2.12), в противном случае – по (2.13).
Иногда в справочниках параметры оборудования задаются не в долевых относительных единицах, а в процентах. В этом случае
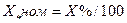 . (2.14)
. (2.14)
В качестве примера, можно указать на реактор, сопротивление которого, как правило, задается в процентах.
2.2.4. Порядок составления схемы замещения
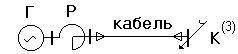 |
Если исходная расчетная схема не содержит трансформаторы, то есть имеет одну ступень напряжения, то при составлении схемы замещения такая схема не нуждается в эквивалентировании, так как все ее элементы находятся на одной и той же ступени напряжения. Например, схема на рис.2.1.
Рис.2.1.
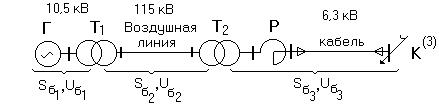 |
Если же расчетная схема имеет вид, приведенный на рис.2.2., то такую схему нужно эквивалентировать, то есть параметры всех элементов схемы следует привести к одной (основной) ступени напряжения. Выбор основной ступени напряжения произволен, однако в ходе решения конкретной задачи он должен оставаться неизменным.
 Рис.2.2.
Рис.2.2.
Для приведения схемы замещения к эквивалентному виду при расчете токов к.з. в относительных единицах следует выбрать значение базисной мощности 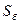 , которая остается одной и той же для всех ступеней напряжения, то есть
, которая остается одной и той же для всех ступеней напряжения, то есть 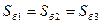 . (2.15)
. (2.15)
Базисные напряжения для каждой ступени напряжения будут иметь различные значения. Для определения базисных напряжений других ступеней напряжения при произвольно принятой ступени напряжения в качестве основной (базисной), следует исходить из общей теории трансформатора и определять их значения по формуле
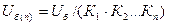 , (2.16)
, (2.16)
где 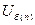 - базисное напряжение
- базисное напряжение 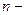 ступени;
ступени; 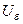 - базисное напряжение ступени, принятую за основную базисную;
- базисное напряжение ступени, принятую за основную базисную; 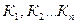 -коэффициенты трансформации трансформаторов на пути от ступени, принятой за основную базисную, к ступени напряжения, базисное напряжение которой определяется.
-коэффициенты трансформации трансформаторов на пути от ступени, принятой за основную базисную, к ступени напряжения, базисное напряжение которой определяется.
Формула (2.16) используется тогда, когда известны коэффициенты трансформации, то есть ведется точное приведение.На практике (при отсутствии действительных значений коэффициентов трансформации) нередко пользуются приближенным методом эквивалентирования, который часто обеспечивает приемлемые результаты. В этом случае за базисные напряжения ступеней принимают средние значения этих ступеней согласно табл.2.1.
Таблица 2.1
Шкала средних номинальных напряжений ступеней
| Ступень напряжения, кВ | Среднее напряжение ступени, принимаемое за базисное, кВ |
| 6,3 | |
| 10,5 | |
2.2.5. Способы приведения схем замещения к простейшему виду
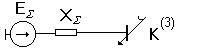 |
Одним из условий расчета токов к.з. является необходимость приведения исходной схемы замещения к простейшему виду (рис.2.3), то есть к получению значений результирующей э.д.с. ЕS и результирующего сопротивления ХS для исходной схемы.
Рис.2.3.
Для этой цели используют методы, известные из курса теоретических основ электротехники (ТОЭ)[1]. Так значения последовательно включенных сопротивлений суммируются, для параллельно включенных –суммируются их проводимости, а для смешанных схем соединений применяют оба способа. Сеть, состоящая из последовательных, параллельных и смешанных схем соединения сопротивлений является простой сетью, и она легко приводится к простейшему виду.
Если сеть содержит замкнутые контуры, то она является сложной, и для приведения ее к простейшему виду следует использовать другие приемы. Рассмотрим некоторые из них.
а)Замена нескольких генераторных ветвей, сходящихся в одной точке, одной эквивалентной.
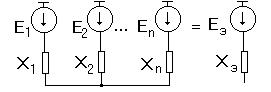 |
Пусть имеется схема замещения (рис.2.4), содержащая
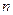 генераторных ветвей, сходящихся в одной точке.
генераторных ветвей, сходящихся в одной точке.
Рис.2.4.
Согласно [1] эквивалентная э.д.с., то есть э.д.с. генератора, которая заменяет э.д.с . 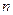 генераторов и эквивалентное сопротивление, могут быть определены по формулам:
генераторов и эквивалентное сопротивление, могут быть определены по формулам:
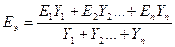 ; (2.17)
; (2.17)
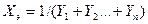 , (2.18)
, (2.18)
где 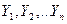 - проводимости генераторных ветвей.
- проводимости генераторных ветвей.
б)Преобразование многолучевой звезды в соответствующий многоугольник
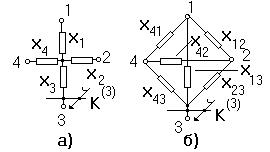 |
В этом случае (рис. 2.5, а), сохраняя опорные точки звезды
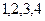 , получают многоугольник (рис.2.5, б)
, получают многоугольник (рис.2.5, б)
Рис.2.5.
Сопротивления сторон многоугольника определяют по формуле
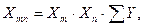 (2.19)
(2.19)
где 
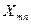 - сопротивление стороны многоугольника
- сопротивление стороны многоугольника  ;
;
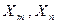 -сопротивления лучей звезды
-сопротивления лучей звезды 
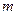 и
и 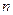 ;
;
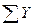 -сумма проводимостей всех лучей звезды.
-сумма проводимостей всех лучей звезды.
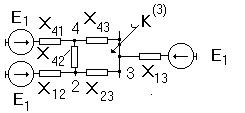 |
Далее, получив многоугольник, рассекают точку
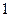 и получают схему (рис.2.6), дальнейшее преобразование которой не вызывает затруднений.
и получают схему (рис.2.6), дальнейшее преобразование которой не вызывает затруднений.
Рис.2.6.
в)Преобразование трехлучевой звезды в треугольник и наоборот (рис.2.7)
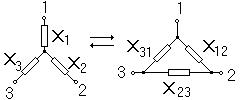 |
Рис.2.7.
В качестве примера приведем формулы для определения 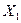 и
и 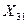
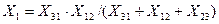 ; (2.20)
; (2.20)
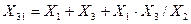 . (2.21)
. (2.21)
г) Металлическое трехфазное к.з. находится в узле с несколькими сходящимися в нем ветвями (рис.2.8, а).
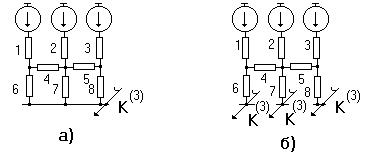 |
В этом случае этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же к.з. Далее полученную схему нетрудно преобразовать относительно любой из точек к.з., учитывая другие ветви с к.з., как нагрузочные с э.д.с, равными нулю (рис.2.8, б).
Рис.2.8.
На практике часто встречается симметрия схемы относительно точки к.з. или симметрия какого-нибудь участка схемы относительно некоторой промежуточной точки. Наличие симметрии позволяет существенно упростить преобразование схемы замещения. Например, если в схеме (рис.2.8,а), элементы, расположенные симметрично относительно элемента 7, одинаковы, то потенциалы узлов, где присоединены ветви 1 и 3, также одинаковы, что позволяет эти узлы закоротить и образовавшиеся параллельные ветви 1 и 3, 4 и 5, 6 и 8 заменить эквивалентными. При этом вместо двух контуров схема теперь содержит один контур, преобразовав который в эквивалентную звезду, просто привести схему к простейшему виду (рис.2.9).
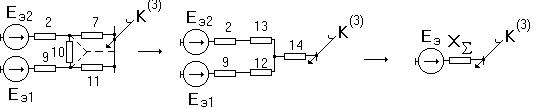 |
Рис.2.9.
Если в схеме рис.2.8 генерирующие ветви 1, 2 и 3 одинаковы, а также одинаковы элементы 6, 7 и 8, то наличие элементов 4 и 5 при рассматриваемом положении точки к.з. никак не сказывается, то есть каждая генерирующая является независимой.
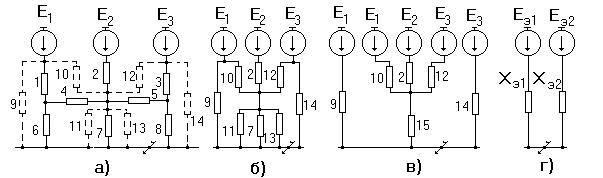
В общем случае, когда элементы рис.2.8 различны (сопротивления и э.д.с.) для ее упрощения можно трехлучевые звезды 1, 4, 6 и 3, 5, 8 заменить эквивалентными треугольниками (рис.2.10, а), затем разрезать их вершины, где приложены э.д.с., и образовавшиеся параллельные ветви (11, 7, 13) заменить эквивалентной (рис.2.10, б, в, г).
Рис.2.10.
д)Разнесение мощностей или токов, подходящих к вершине треугольника сопротивлений (рис.2.11, а, б) по ветвям разомкнутого треугольника (рис.2.11, в)
При разнесении мощности расчетные соотношения имеют вид:
 |
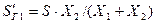 ;
; 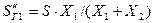 ;
; 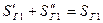 . (2.22)
. (2.22)
Рис.2.11.
a-исходная принципиальная схема;б-схема замещения;
в-схема замещения после преобразования
При расчете линейных электрических цепей часто удобно использовать принцип наложения. Согласно этому принципу действительный режим получают как результат наложения ряда условных режимов, каждый из которых определяется в предположении, что в схеме приложена одна (или группа) э.д.с., в то время как все остальные равны нулю; при этом все элементы схемы замещения остаются включенными.
При большом числе э.д.с. расчет токов к.з. при применении принципа наложения в такой форме становится громоздким и слишком неудобным.
В этой связи при рачете токов к.з. обычно используют следующие формы принципа наложения:
1)Наложение собственно аварийного режима на предшествующий
Дело в том, что условия металлического трехфазного к.з. не изменятся, если представить, что в точке к.з. приложены две равные, но взаимно противоположные э.д.с, величина которых может быть произвольной. В частности, ее можно принять раной напряжению, которое было в этой точке до возникновения в ней к.з.
При таком подходе режим в схеме замещения после возникновения к.з. удобно представить состоящим из двух режимов.
Первый режим получают, учитывая все э.д.с. генераторов до возникновения к.з., и дополнительную э.д.с., введенную в точку к.з., равную 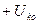 (
( 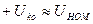 в данной точке).
в данной точке).
Очевидно, то одновременное действие этих э.д.с. дает предшествующий режим в рассматриваемой схеме замещения.
Второй режим получают путем введения только одной э.д.с. в точке к.з., равной 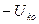 . Этот режим называют собственно аварийным, а получающиеся при нем токи и напряжения – аварийными составляющими токов и напряжений.
. Этот режим называют собственно аварийным, а получающиеся при нем токи и напряжения – аварийными составляющими токов и напряжений.
Суммируя токи и напряжения предшествующего режима с их аварийными составляющими, получают действительные величины токов и напряжений в схеме замещения при металлическом трехфазном к.з. в заданной точке, то есть
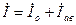 ;
; 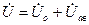 . (2.23)
. (2.23)
Здесь 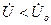 , так как
, так как 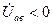 .
.
2)Применение собственных и взаимных сопротивлений и проводимостей
В схеме с произвольным числом э.д.с. 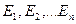 для тока, например, источника 1, считая положительным направлением тока путь от источника к внешней сети, по принципу наложения можно записать:
для тока, например, источника 1, считая положительным направлением тока путь от источника к внешней сети, по принципу наложения можно записать:
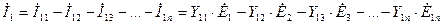 , (2.24)
, (2.24)
где каждый из токов обусловлен действием лишь одной э.д.с. при равенстве нулю остальных, то есть 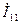 - собственный ток источника 1, созданный только его э.д.с.
- собственный ток источника 1, созданный только его э.д.с. 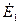 ;
; 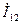 - взаимный ток ветви 1, вызванный действием только э.д.с.
- взаимный ток ветви 1, вызванный действием только э.д.с. 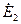 и т.д.
и т.д.
Здесь 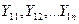 - соответственно, собственная и взаимные проводимости источника 1 в рассматриваемой схеме.
- соответственно, собственная и взаимные проводимости источника 1 в рассматриваемой схеме.
Аналогично для тока в месте к.з. (считая, что в месте металлического трехфазного к.з. имеется источник с э.д.с., равной нулю) получим
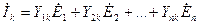 , (2.25)
, (2.25)
где 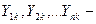 взаимные проводимости между каждым источником и точкой к.з.
взаимные проводимости между каждым источником и точкой к.з.
Выражения (2.24) и (2.25) особенно удобны, когда нужно выявить индивидуальные свойства отдельных источников или учесть влияние изменения величины и фазы отдельных э.д.с. на искомые значения токов.
Собственные и взаимные сопротивления или проводимости находят с помощью так называемого способа токораспределения ( или называемый методом единичных токов) или путем преобразования исходной схемы замещения. Иногда целесообразно использовать оба приема совместно, то есть вначале произвести ряд преобразований схемы, а затем применить метод токораспределения.
В расчетах к.з. часто приходится определять только взаимные сопротивления между точкой к.з. и отдельными источниками (или группами их). Для этого удобно использовать следующий прием. Приняв ток в месте к.з. за единицу и считая все приведенные э.д.с. одинаковыми, нужно произвести распределение этого тока (равного единице) в заданной схеме замещения. Полученные доли этой единицы для отдельных источников: С 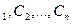 , называемые коэффициентами распределения, при отсутствии нагрузок в схеме они характеризуют участия каждого источника в питании к.з. Если результирующее сопротивление схемы относительно места к.з.
, называемые коэффициентами распределения, при отсутствии нагрузок в схеме они характеризуют участия каждого источника в питании к.з. Если результирующее сопротивление схемы относительно места к.з. 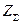 , то, очевидно, можно записать равенства:
, то, очевидно, можно записать равенства:
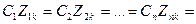 1. ZS, (2.26)
1. ZS, (2.26)
откуда искомое взаимное сопротивление между точкой к.з. и соответ-
ствующим источником будет:
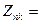 ZS/Сn. (2.27)
ZS/Сn. (2.27)
3. ЭЛЕКТРОМАГНИТНЫЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ
ПРИ СОХРАНЕНИИ СИММЕТРИИ ТРЕХФАЗНОЙ ЦЕПИ
3.1. ПЕРЕХОДНЫЙ ПРОЦЕСС В ПРОСТЕЙШИХ ТРЕХФАЗНЫХ ЦЕПЯХ
3.1.1. Постановка задачи и ее ограничения
Симметричную трехфазную цепь с сосредоточенными активными сопротивлениями и индуктивностями при отсутствии в ней трансформатор-
ных связей условимся называть простейшей трехфазной цепью.
Электромагнитный переходный процесс в такой цепи рассмотрим сначала при условии, что ее питание осуществляется от источника, собственное сопротивление которого равно нулю и его напряжение, изменяясь с постоянной частотой, имеет неизменную амплитуду.
Включение в схему такого источника соответствует теоретическому пределу, когда изменение внешних условий не влияет на работу самого источника.
3.1.2. Анализ трехфазного к.з в неразветвленной простейшей цепи
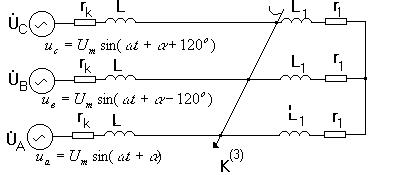 |
Рассмотрим схему замещения (рис.3.1.) Как видно, она является симмеричной, так как сопротивления всех трех фаз равны между собой.
Рис.3.1.
Предположим, что до к.з. в схеме протекал процесс, характеризуемый параметрами 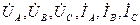 . При этом для мгновенного значения тока фазы
. При этом для мгновенного значения тока фазы  можно записать
можно записать 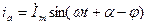 .
.
Допустим, что произошло металлическое трехфазное к.з. так, что схема распалась на две независимые части.
После этого в левой части схемы наступит новый установившийся режим, характеризуемый параметрами: 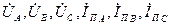 , где
, где 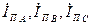 -
-
установившиеся значения токов фаз.
Построим векторную диаграмму, характеризующую режим левой части схемы до к.з. и после к.з. (рис.3.2), где ось  - есть ось времени.
- есть ось времени.
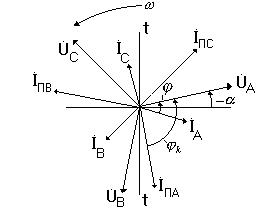 |
Рис.3.2.
Следует отметить, что в новом режиме фаза и величина токов изменились в сторону увеличения. Увеличение фазы (углового сдвига тока относительно напряжения своей фазы) обусловлено увеличением доли реактивной составляющей сопротивления цепи к.з. по сравнению с ее активной составляющей (сказывается отсутствие сопротивления нагрузок, имеющего преимущественно активную составляющую сопротивления с целью получения высокого значения коэффициента мощности).
Дата добавления: 2016-04-14; просмотров: 2102;
