Построение коммутационных схем на основе алгебры логики

Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они широко используются в технике автоматического управления, в электронно-вычислительной технике, и т. д.

Эти устройства (их в общем случае называют переключательными, или ком­мутационными, схемами) содержат сотни реле, полупроводниковых элементов и других переключающих элементов. Описание и конструирование таких схем в силу их большого объема представляет трудную задачу.

Еще в 1910 году физик П. С. Эренфест указал на возможность применения ап­парата алгебры логики при исследовании релейно-контактных схем. Однако его идеи начали реализовываться значительно позже, когда создание общей теории конструирования таких схем стало остро необходимым.

Использование алгебры логики в конструировании коммутационных схем оказалось возможным в связи с тем, что каждой схеме можно поставить в соот­ветствие некоторую формулу алгебры логики и каждая формула алгебры логики реализуется с помощью некоторой схемы. Это обстоятельство помогает выявить возможности упрощения заданной схемы, изучая соответствующую формулу, а упрощение формулы затем реализовать как упрощение схемы.

В то же время еще до построения схемы можно заранее описать с помощью формул те функции, которые схема должна выполнять. Рассмотрим, как устанав­ливается связь между формулами алгебры логики и переключательными схемами.

Под переключательной схемой понимается схематическое изображение неко­торого устройства, состоящего из

□ переключателей;

□ соединительных проводников;

□ входов в схему и выходов из нее.

Переключателями могут быть электромеханические устройства (выключатели, переключатели, кнопки), электромагнитные реле, полупроводниковые элементы и т. п., а входами и выходами — клеммы, на которые подается электрическое на­пряжение.

Коммутационной схемой принимается в расчет только два состояния каждого переключателя, которые называются «замкнутым» и «разомкнутым».

Рассмотрим схему переключения, состоящую из источника питания и электри­ческой лампочки (рис. 4.1).

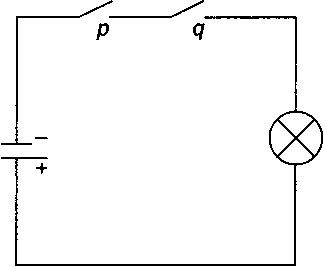Рис. 4.1. Схема с последовательным соединением переключателей

Присвоим значение 1 переключателям р и q, если они замкнуты (то есть элек­трический ток проходит через них). В противоположной ситуации присвоим им значение 0. Присвоим значение 1 схеме, когда лампочка светится (то есть элек­трический ток через нее проходит). Заметим, что при последовательном соеди­нении элементов цепи pnq, как это имеет место на приведенной схеме, лампочка загорается и значение схемы становится равным 1 только в том случае, когда оба переключателя замкнуты, то есть когда и р, и q имеют значение 1. Таким образом, схема соответствует высказыванию р д q. Такое расположение переключателей называется логическим элементом р и q, или схемой логического умножения. Этот логический элемент обозначается символом, изображенным на рис. 4.2.

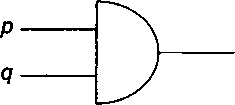Рис. 4.2. Элемент логического умножения

Рассмотрим схему переключения, показанную на рис. 4.3, где переключатели р и q соединены параллельно.

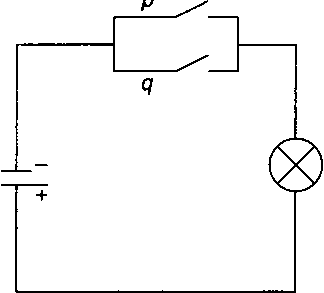Рис. 4.3. Схема с параллельным соединением переключателей

Отметим, что лампочка загорается и значение схемы становится равным 1, когда один из двух переключателей (р или q) замкнут, то есть либо р = 1, либо <7=1 (либо оба они равны 1). Эта схема соответствует высказыванию pvq. Такое расположение переключателей называется логическим элементом р или q, или схемой логического сложения. Этот логический элемент обозначается символом, изображенным на рис. 4.4.

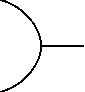
Рис. 4.4. Элемент логического сложения

Предположим, имеется схема с одним переключателем р, который обладает та­ким свойством, что лампочка загорается тогда и только тогда, когда переключатель разомкнут. Следовательно, схема имеет значение 1, когда р равно 0, и значение О, когда р равно 1. Эта схема соответствует р, а соответствующий логический элемент называется логическим элементом не, или инвертором (рис. 4.5).

Рис. 4.5. Инвертор

Пример. Схема на рис. 4.6 содержит логический элемент puq, за которым следует инвертор, так что схема соответствует выражению р д q. Заметим, что инвертор отрицает всю предшествующую ему схему. 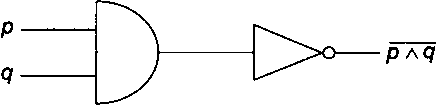Рис. 4.6. Логическая схема р л q

Пример. Схема на рис. 4.7 содержит соединение логического элемента р или q с логическим элементом не г посредством логической схемы умножения. Следо­вательно, она соответствует выражению (pv q) г.

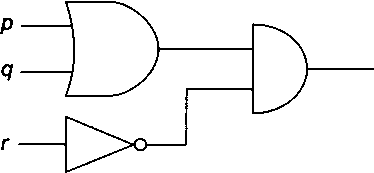Рис. 4.7. Логическая схема (р v q) л г

Из трех логических элементов, соответствующих выражениям сложения, ум­ножения и отрицания в булевой алгебре, можно строить электронные логические схемы любой сложности.

На практике часто встречаются обозначения, принятые для цифровых микро­схем:

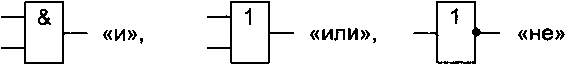
Вопросы для самопроверки

1. Почему изучение логических основ так важно для понимания информатики?

2. Дайте определение понятию простого высказывания. Приведите примеры.

3. Является ли предложение «Который сейчас час?» простым высказыванием с точки зрения математической логики?

4. Какие логические операции над высказываниями вам известны?

5. Дайте определение конъюнкции и дизъюнкции, приведите примеры.

6. Дайте определение импликации и эквивалентности, приведите примеры.

7. Дайте определение формулы алгебры логики.

8. Какие формулы алгебры логики называются равносильными?

9. Приведите формулы законов идемпотентности.

10. Приведите формулы законов поглощения.

11. Как записывается и чем примечательна логическая операция Штрих Шеффера?

12. Какими формулами записываются законы идемпотентности в булевой алгебре?

13. Дайте определение функции Буля.

14. Что такое «переключательная (коммутационная) схема»?

15. Нарисуйте коммутационную схему, реализующую логическую операцию И.

16. Нарисуйте коммутационную схему, реализующую логическую операцию ИЛИ.

17. Чем важна булева алгебра для информатики и компьютерной техники?

Литература

1. Аляев Ю. А.у Тюрин С. Ф. Дискретная математика и математическая логика. M.: Финансы и статистика, 2006.

2. Верещагин Н. К., Плиско Н. К., Успенский В. А. Вводный курс математической логики. M.: Физматлит, 2004.

3. Новиков Ф. А. Дискретная математика для программистов. СПб.: Питер, 2003.