Крутящий момент на валу радиально-поршневой гидромашины
При работе радиально-поршневой машины на ее блоке цилиндров возникает крутящий момент, который в насосе преодолевается приводным двигателем, а в гидромоторе приводит во вращательное движение ротор машины. Возникает крутящий момент на блоке цилиндров в результате давления рабочей жидкости на поршни гидромашины.
Теоретический крутящий момент радиально-поршневой машины, как и других объемных гидромашин, определяется по зависимости (3.4), которая для данного случая с учетом (5.2) принимает следующий вид:
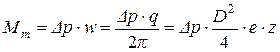 .
.
Для определения текущего крутящего момента рассмотрим силы, которые действуют в точке контакта поршня с внутренней поверхностью статорного кольца.
Сила давления жидкости на поршень цилиндра, который в данный момент соединен с полостью нагнетания насоса (рабочей полостью гидромотора), направлена по его оси (рис. 5.9) и равняется
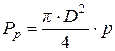 ,
,
где  – давление жидкости.
– давление жидкости.
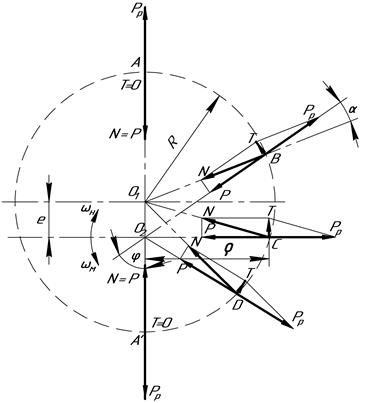
Рис. 5.9. Схема действия сил в радиально-поршневой гидромашине
На схеме действия сил в радиально-поршневой гидромашине (рис. 5.9) условно, с целью незагромождения рисунка, не приведены контуры ротора, распределителя жидкости, поршня и другие конструктивные элементы, а основные буквенные обозначения отвечают принятым на рис. 5.3.
В точке контакта  (рис. 5.9) поршня со статорным кольцом (допускаем, что эта точка находится на осе поршня) возникает нормальная к поверхности кольца и направлена к его центру
(рис. 5.9) поршня со статорным кольцом (допускаем, что эта точка находится на осе поршня) возникает нормальная к поверхности кольца и направлена к его центру  сила
сила 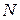 реакции, которую можно разложить на составляющие:
реакции, которую можно разложить на составляющие: 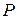 – направленную по оси поршня к центру ротора
– направленную по оси поршня к центру ротора 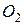 ,
, 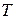 – направленную перпендикулярно к оси последнего.
– направленную перпендикулярно к оси последнего.
Так как поршень относительно продольной оси  находится в равновесии, то составляющая
находится в равновесии, то составляющая 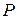 равна по величине и обратная по направлению сумме сил, которые действуют со стороны поршня по его оси. К указанным силам относятся сила давления жидкости на поршень
равна по величине и обратная по направлению сумме сил, которые действуют со стороны поршня по его оси. К указанным силам относятся сила давления жидкости на поршень 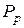 , усилие сжатия пружины
, усилие сжатия пружины  , сила инерции поршня в относительном движении
, сила инерции поршня в относительном движении 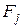 , сила трения
, сила трения 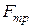 и др., Принимая, что
и др., Принимая, что  , будем считать
, будем считать 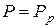 .
.
Нормальная к оси поршня  составляющая
составляющая 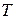 создает крутящий момент, который для условий приведенной схемы (рис. 5.9) в гидромоторе вращает ротор против часовой стрелки с угловой скоростью
создает крутящий момент, который для условий приведенной схемы (рис. 5.9) в гидромоторе вращает ротор против часовой стрелки с угловой скоростью 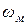 , а в условиях насоса преодолевается поводом при угловой скорости
, а в условиях насоса преодолевается поводом при угловой скорости 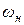 .
.
Из выше принятого условия 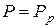 правомерные следующие зависимости (рис. 5.9)
правомерные следующие зависимости (рис. 5.9)
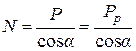 , (5.13)
, (5.13)
но
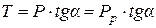 . (5.14)
. (5.14)
Согласно схемы  , откуда
, откуда
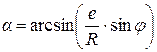 .
.
Подставив значение угла 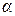 в выражения (5.13) и (5.14), получим
в выражения (5.13) и (5.14), получим
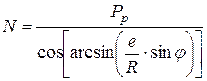 ;
;
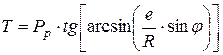 .
.
Таким образом, при постоянстве значения силы 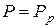 , значения сил
, значения сил 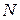 и
и 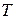 изменяются в зависимости от угла повороту ротора
изменяются в зависимости от угла повороту ротора 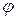 (рис. 5.9). Так, при
(рис. 5.9). Так, при 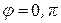 (точки контакта поршня со статорным кольцом
(точки контакта поршня со статорным кольцом 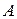 і
і  ) нормальная составляющая
) нормальная составляющая  , а
, а 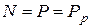 . Максимальных значений силы
. Максимальных значений силы 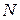 и
и 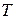 достигают при
достигают при 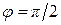 (точка контакта
(точка контакта 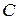 ). При промежуточных значениях угла поворота
). При промежуточных значениях угла поворота 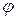 (точки контакта
(точки контакта 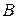 и
и 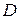 ) силы
) силы 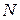 и
и 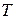 также принимают промежуточные значения.
также принимают промежуточные значения.
Сила реакции 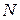 нагружает подшипники статорного кольца, а также определяет величину контактного напряжения на головке плунжера и внутренней поверхности этого кольца.
нагружает подшипники статорного кольца, а также определяет величину контактного напряжения на головке плунжера и внутренней поверхности этого кольца.
Текущее значение крутящего момента, который возникает на одном поршне радиально-поршневой гидромашины, определяется зависимостью
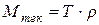 , (5.15)
, (5.15)
где 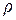 – мгновенное значение плеча силы
– мгновенное значение плеча силы 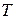 , ровное расстоянию от центра
, ровное расстоянию от центра 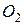 вращения блока цилиндров до точки приложения этой силы.
вращения блока цилиндров до точки приложения этой силы.
Согласно схемы действия сил (рис. 5.9) и кинематической схемы (рис. 5.3) радиально-поршневой гидромашины
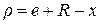 ,
,
а с учетом (5.9)
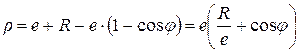 . (5.16)
. (5.16)
Преобразуем выражение (5.15) к виду
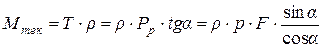 . (5.17)
. (5.17)
Так как 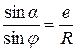 , то при
, то при 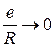
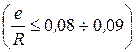 значение
значение 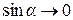 и правомерно принять
и правомерно принять 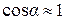 . Тогда с учетом
. Тогда с учетом 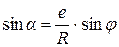 выражение (5.17) приобретает вид
выражение (5.17) приобретает вид
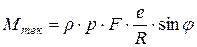 . (5.18)
. (5.18)
Если в выражение (5.18) подставить значение плеча 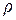 из (5.16), то с учетом
из (5.16), то с учетом 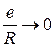 получим
получим
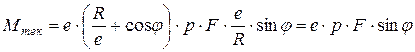 . (5.19)
. (5.19)
Таким образом, момент 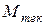 изменяется при вращении ротора по синусоидальному закону, как и текущая подача поршня (5.12). При
изменяется при вращении ротора по синусоидальному закону, как и текущая подача поршня (5.12). При 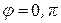 значение момента
значение момента 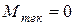 , потому невозможно создать гидромотор с одним, или двумя диаметрально противоположно расположенными поршнями.
, потому невозможно создать гидромотор с одним, или двумя диаметрально противоположно расположенными поршнями.
Суммарный текущий момент на валу гидромашины равняется сумме текущих моментов 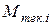 , которые развиваются поршнями цилиндров в количестве
, которые развиваются поршнями цилиндров в количестве 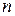 , какие в данный момент соединенные с полостью нагнетания насоса (рабочей полостью гидромотора)
, какие в данный момент соединенные с полостью нагнетания насоса (рабочей полостью гидромотора)
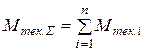 . (5.20)
. (5.20)
Из (5.19) и (5.20) также следует, что крутящий момент гидромашины снижается при уменьшении эксцентриситета 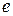 . Поэтому при некотором малом значении эксцентриситета крутящий момент гидромотора станет сравнимым с потерями холостого хода
. Поэтому при некотором малом значении эксцентриситета крутящий момент гидромотора станет сравнимым с потерями холостого хода 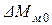 (рис. 3.9), в результате чего произойдет его самозатормаживание даже без нагрузки.
(рис. 3.9), в результате чего произойдет его самозатормаживание даже без нагрузки.
Дата добавления: 2016-04-14; просмотров: 2035;
