Собственные затухающие колебания

В реальных колебательных контурах омическое сопротивление всегда отлично от нуля. Вследствие этого энергия, первоначально запасенная в контуре, непрерывно расходуется на выделение теплоты, что приводит к затуханию собственных колебаний.

Найдем дифференциальное уравнение затухающих колебаний. Для этого рассмотрим контур, содержащий, кроме индуктивности L и емкости С, омическое сопротивление R . Зарядим конденсатор до напряжения U₀ , затем цепь замкнем. При разрядке конденсатора в цепи возникнет ток i , изменяющийся со временем. На основании второго закона Кирхгофа для данного контура можно записать

.

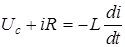В этом выражении сделаем замену величинU_c, i :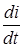

.

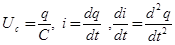Тогда получим:

.

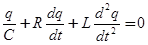Разделив левую и правую части на L и обозначив

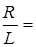2b , ,

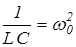получим дифференциальное уравнение собственных затухающих колебаний

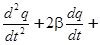w₀ ² q = 0. (7)

Решением этого уравнения является колебание вида

q = q₀ e ^{b t}cos (w + j ), (8)

где (w + j ) - фаза колебаний, j- начальная фаза колебаний, q₀ e^{b t} - амплитуда колебаний ,w- циклическая частота затухающих колебаний, численно равная числу полных колебаний, совершаемых системой за 2p секунд.

Амплитуда колебаний

А = q₀ e^{b t}

не является постоянной величиной, а с течением времени непрерывно убывает. Быстрота убывания амплитуды колебаний определяется коэффициентом затухания

b = ,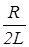

который численно равен обратной величине времени, в течение которого амплитуда колебаний убывает в е раз.

Для количественной характеристики затухания колебаний пользуются логарифмическим декрементом затухания d, который равен натуральному логарифму отношения двух последовательных амплитуд, отличающихся по времени на один период:

d=ln .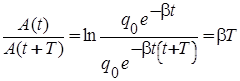

Циклическая частота собственных затухающих колебаний w связана с частотой собственных незатухающих колебаний w₀ соотношением

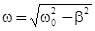. (9)

Период затухающих колебаний равен

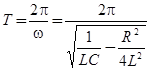(10)

Из (9) и (10) видно, что для собственных затухающих колебаний циклическая частота меньше, а период больше соответствующих частоты и периода собственных незатухающих колебаний. С увеличением сопротивления контура R период собственных колебаний возрастает и при выполнении условия

,

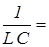
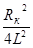где

,

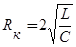обращается в бесконечность. Это сопротивление называется критическим. Оно зависит от величины емкости и индуктивности. Если сопротивление контура превышает R_к ,то электрические колебания не возникают и заряд конденсатора уменьшается монотонно, асимптотически приближаясь к нулю. Такой разряд конденсатора называется апериодическим.

Наряду с зарядом, напряжение на обкладках конденсатора и сила тока в цепи тоже совершают затухающие колебания с тем же периодом. Напряжение и ток будут изменяться по следующим законам:

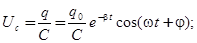
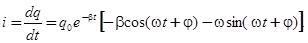(11)

Путем преобразований выражение (11) можно привести к виду:

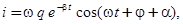
где

a- сдвиг фаз тока и напряжения.

Колебательный контур характеризуется добротностью Q , которая вычисляется по формуле

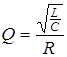. (12)

Экспериментально добротность может быть найдена по затуханию как отношение числа p к логарифмическому декременту затухания:

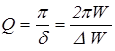. (13)

В данной работе требуется изучить зависимость периода Т и добротности Q линейного колебательного контура от его параметров L, C, R.

Описание установки

Для наблюдения свободных электрических колебаний используется установка, изображенная на рис.3.

Установка состоит из генератора прямоугольных импульсов Г, регулируемого сопротивления R, индуктивности L, регулируемого конденсатора С, индуктивности L₁ и осциллографа О. Осциллограф служит для записи осциллограммы напряжения.