Колебания в колебательном контуре.
ИЗУЧЕНИЕ КОЛЕБАТЕЛЬНОГО КОНТУРА
Колебательные процессы широко распространены в природе и технике. Примером колебаний различных физических величин являются колебания маятников, струн, мембран телефонов, звук, свет, а также переменный электрический ток, представляющий собой электрические колебания. Для всех этих явлений характерна общность закономерностей и математических методов исследования. Так, например, процессы, протекающие при электрических колебаниях, аналогичны процессам, протекающим при механических колебаниях.
Простейшей колебательной системой в механике является груз, подвешенный на пружине и движущийся без трения . Груз, выведенный из положения равновесия, совершает гармонические колебания, при которых смещение из положения равновесия изменяется со временем по закону синуса. Когда груз находится в крайних положениях , его кинетическая энергия равна нулю, а потенциальная энергия достигает максимального значения. При прохождении грузом положения равновесия потенциальная энергия становится минимальной, а кинетическая энергия груза достигает максимального значения. Мы имеем в данном случае периодическое превращение кинетической энергии системы в потенциальную и обратно. Подобные превращения энергии наблюдаются и при электрических колебаниях.
Электрические колебания могут возникнуть в замкнутой цепи, содержащей индуктивность и емкость. Такая цепь называется колебательным контуром (рис.1)
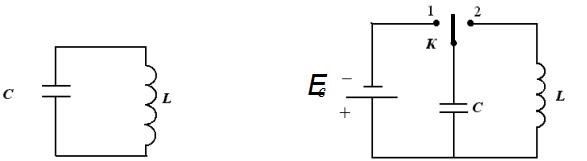
Рис. 1 Рис. 2
Рассмотрим колебательный контур, состоящий из конденсатора емкости С , катушки с индуктивностью L и ключа К (рис. 2). Предположим, что омическое сопротивление цепи равно нулю. В положении 1 ключа К зарядим конденсатор до разности потенциалов j1 - j2 = Uc ,где j1 и j2 – потенциалы обкладок конденсатора. На обкладках конденсатора появятся разноименные заряды величины q0 , и между обкладками возникнет электрическое поле, энергия которого равна
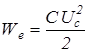 .
.
Если замкнуть ключ К в положении 2, то конденсатор начнет разряжаться, в цепи возникнет электрический ток i , изменяющийся с течением времени. Наличие тока в цепи приведет к возникновению магнитного поля, которое в основном будет сосредоточено внутри катушки. Энергия электрического поля будет уменьшаться со временем, а энергия магнитного поля – увеличиваться. Через некоторое время конденсатор разрядится полностью, электрическое поле исчезнет совсем, а энергия магнитного поля достигнет максимального значения:

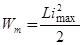
 .
. 
При этом вся энергия электрического поля превратится в энергию магнитного поля. Далее ток и энергия магнитного поля уменьшаются, конденсатор перезаряжается и между его обкладками возникает электрическое поле противоположного направления, энергия магнитного поля превращается в энергию электрического поля. В дальнейшем те же процессы будут протекать в обратном порядке, система придет в первоначальное состояние, и весь процесс будет повторяться снова. Таким образом, в контуре возникают электрические колебания заряда на обкладках конденсатора, напряжения на конденсаторе и силы тока в цепи. Колебания сопровождаются взаимными превращениями энергий электрического и магнитного полей. Такие колебания, происходящие под действием процессов в самом колебательном контуре, называются собственными колебаниями. Если омическое сопротивление контура равно нулю, то процесс периодического превращения электрической энергии в магнитную и обратно будет продолжаться сколь угодно долго, т.е. колебания не затухают.
Собственные незатухающие колебания можно описать с помощью математических уравнений. Будем считать, что ток, текущий в контуре при разрядке конденсатора, квазистационарный, т.е. в каждый момент времени сила тока во всех сечениях контура одинакова. Применим для рассматриваемого контура второй закон Кирхгофа, согласно которому сумма падений напряжения в контуре равна сумме действующих в нем ЭДС
Uc = Ec , (1)
где Ec - ЭДС самоиндукции. Учитывая, что
Ec = 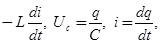
уравнение (1) перепишем в виде
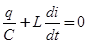 ,
,
или
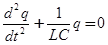 .
.
Обозначив 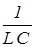 через w02 , получим дифференциальное уравнение собственных незатухающих колебаний
через w02 , получим дифференциальное уравнение собственных незатухающих колебаний
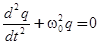 . (2)
. (2)
Решением этого уравнения является функция
q = q0 cos(w0 t + j), (3)
показывающая, что заряд на обкладках конденсатора изменяется по гармоническому закону. В (3) q0 - амплитуда колебаний заряда, j - начальная фаза, а w0 - частота собственных незатухающих колебаний, равная
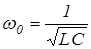 .
.
Период собственных незатухающих колебаний равен:
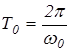 ,
,
или
Т0 = 2p 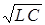 . (4)
. (4)
(4) называется формулой Томсона.
Одновременно с зарядом колеблются напряжение на обкладках конденсатора и сила тока в цепи. Эти колебания совершаются по следующим законам:
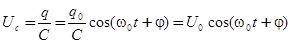 ; (5)
; (5)
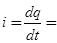 -q0 w0 sin(w0 t + j )= = i0 cos(w0 t + j + p/2), (6)
-q0 w0 sin(w0 t + j )= = i0 cos(w0 t + j + p/2), (6)
где U0 - амплитуда напряжения, i0 =- амплитудное значение тока.
Из (3), (5) и (6) видим, что сила тока, заряд и напряжение изменяются по гармоническому закону. Но между напряжением и током существует разность фаз.
Дата добавления: 2016-04-14; просмотров: 2219;
