Затухающие колебания. В реальных системах, всегда присутствуют процессы, связанные с потерями энергии при действии сил сопротивления (трения)

В реальных системах, всегда присутствуют процессы, связанные с потерями энергии при действии сил сопротивления (трения). Представим силу сопротивления в виде

F_тр = - ru = - r ,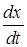

где r - коэффициент сопротивления; u - скорость движения.

Запишем уравнение для маятника с учетом силы сопротивления

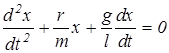.(3)

Введем обозначение

.

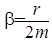Эта величина называетсякоэффициентом затухания . С учетом этого и выражения для w₀ получим

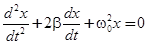. (4)

(4) является дифференциальным уравнением затухающих колебаний.

Решением его будет

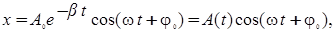(5)

где

,

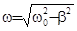А(t)- амплитуда затухающих колебаний в момент времени t, А₀-начальная амплитуда колебаний, w- круговая частота затухающих колебаний. Как видно из формулы, с ростом коэффициента затухания частота уменьшается, следовательно, период колебаний растет. Амплитуда колебаний с течением времени уменьшается по экспоненциальному закону. Отношение амплитуды в момент времени t к амплитуде в момент времени (t+T) называется декрементом затухания. Запишем это определение в виде

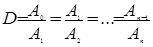. (6)

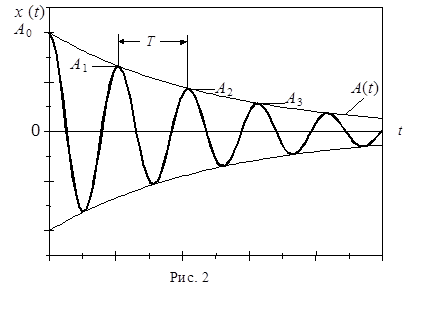
Логарифмическим декрементом называется величина

d=lnD. (7)

Для определения амплитуды колебаний в момент времени t= nT воспользуемся формулой (6)

.

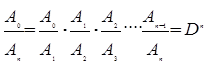Логарифмируя обе части этого выражения, получим

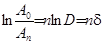. (8)

Из (8) вытекают формулы:

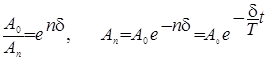. (9)

Если учесть выражение

,

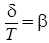то из (9) получится

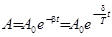. (10)

Cкорость затухания колебаний определяется временем релаксации t. Время, в течение которого амплитуда убывает в e раз называется временем релаксации (e- основание натуральных логарифмов). Найдем его из выражения

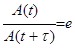. (11)

Подстановка в (11) выражения (10) дает

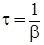(12)

Добротностью колебательной системы Q называется отношение энергии W₀, запасенной в системе, к энергии D W, растрачиваемой за 1 период колебаний, умноженное на p, т.е.

Q=p 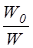(13)

Можно показать, что добротность может быть определена и из формулы:

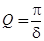(14)