Гармонические колебания

ИЗУЧЕНИЕ МЕХАНИЧЕСКИХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Колебаниями называются процессы (движения или изменения состояния), в той или иной степени повторяющиеся во времени. В зависимости от физической природы колебательного процесса и «механизма» его возбуждения различают: механические колебания (колебания маятников, струн, частей машин и механизмов, зданий мостов, и других сооружений, давления воздуха при распространении в нем воздуха, качка корабля, волнение моря и т.п.); электромагнитные (колебания переменного электрического тока в цепи , колебания векторов Е и В электрической напряженности и магнитной индукции переменного электромагнитного поля и т.д.); электромеханические (колебания мембраны телефона, диффузора электродинамического громкоговорителя и т.п.) и др.

Система, совершающая колебания, называется колебательной.

Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния ее устойчивого равновесия.

Колебания называются периодическими, если значения всех физических величин, характеризующих колебательную систему и изменяющихся при ее колебаниях, повторяются через равные промежутки времени. Наименьший промежуток времени Т, удовлетворяющий этому условию, называется периодом колебаний. За период колебаний Т система совершает одно полное колебание. Частотой периодических колебаний называется величина n=1/Т, равная числу полных колебаний, совершающихся за единицу времени. Циклической (круговой) частотой периодических колебаний называется величина w₀=2pn=2p/Т, равная числу полных колебаний, совершающихся за 2p единиц времени.

При периодических колебаниях зависимость колеблющейся величины х от времени t удовлетворяет условию х(t+Т)=х(t).

Периодические колебания величины х(t) называются гармоническими, если

х(t)=А sin(w₀t+j₀), (1)

где w₀=2pn=(2p/Т)=const-циклическая (круговая) частота гармонических колебаний; А=х_макс=const>0- максимальное значение колеблющейся величины х, называемое амплитудой колебаний; j₀- постоянная величина. Значение х в произвольный момент времени t определяется значением фазы колебаний Ф(t)=w₀t+j₀. Величина j₀ представляет собой начальную фазу колебаний, т.е. значение Ф(t) в момент t=0.

Возьмем вторую производную х:

.

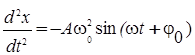Отсюда и из (1) следует, что гармонически колеблющаяся величина х удовлетворяет дифференциальному уравнению

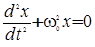(2).

Таким образом, х совершает гармонические колебания в том и только в том случае, если она удовлетворяет уравнению (2), называемому дифференциальным уравнением гармонических колебаний. Величину w₀ часто называют собственной частотой, она равна 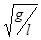в случае математического маятника, 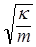- в случае пружинного маятника, где к - коэффициент жесткости пружины и 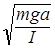- в случае физического маятника, где I его момент инерции, а-расстояние от оси вращения до центра тяжести тела.