Примеры решения задач. 1. Вычислить криволинейный интеграл второго рода , где L − дуга параболы от точки А (0; 0) до точки В (2; 4).
1. Вычислить криволинейный интеграл второго рода 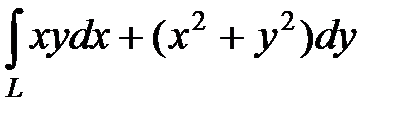 , где L − дуга параболы
, где L − дуга параболы 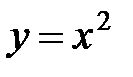 от точки А (0; 0) до точки В (2; 4).
от точки А (0; 0) до точки В (2; 4).
► Применим формулу
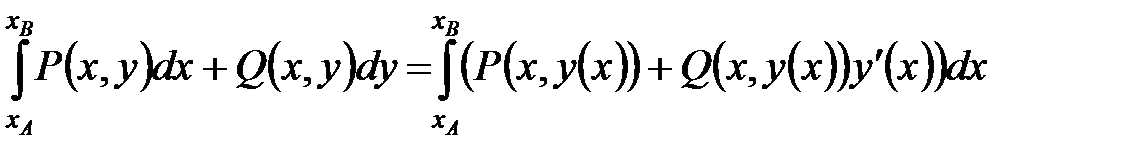 (5.4)
(5.4)
для кривой, заданной уравнением 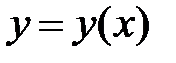 с начальной точкой кривой
с начальной точкой кривой 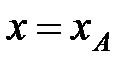 , конечной точкой
, конечной точкой 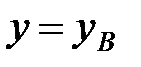 .
.
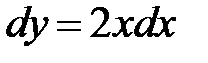 , тогда
, тогда
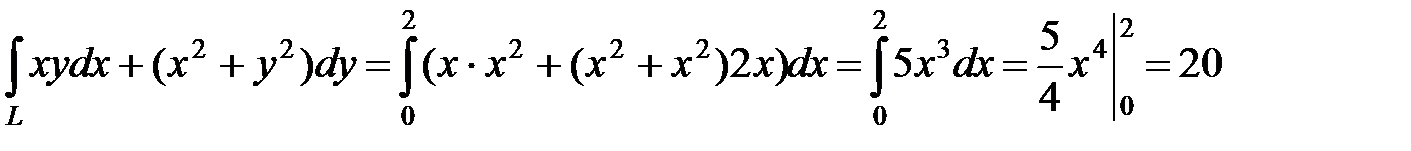 .◄
.◄
2. Вычислить криволинейный интеграл по формуле Грина
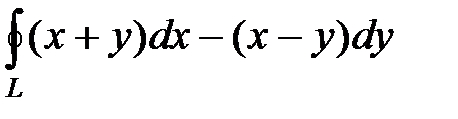 , где L − окружность
, где L − окружность 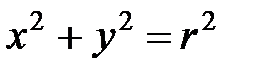 .
.
► Формула Грина
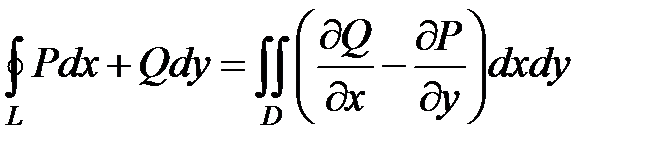 , (5.5)
, (5.5)
где 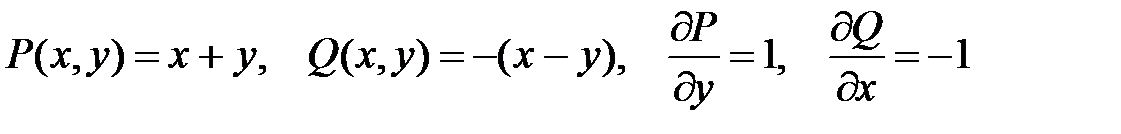 .
.
Тогда
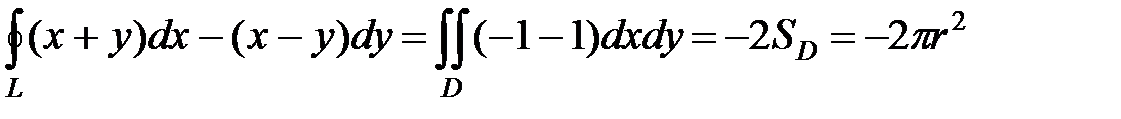 .◄
.◄
Задания для самостоятельной работы
6.2. Вычислить криволинейные интегралы второго рода:
1) 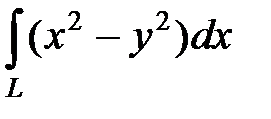 , где L − дуга параболы
, где L − дуга параболы 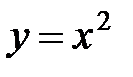 от точки О (0; 0) до точки А (2; 4);
от точки О (0; 0) до точки А (2; 4);
2) 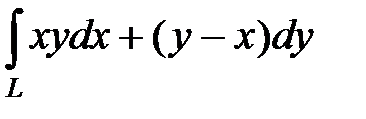 , где L:
, где L: 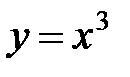 от точки О (0; 0) до точки А (1; 1);
от точки О (0; 0) до точки А (1; 1);
3) 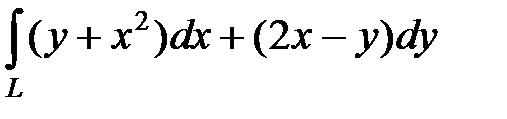 , где L − дуга параболы
, где L − дуга параболы 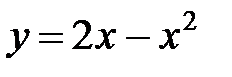 от точки А (1; 1) до точки В (3; -3);
от точки А (1; 1) до точки В (3; -3);
4) 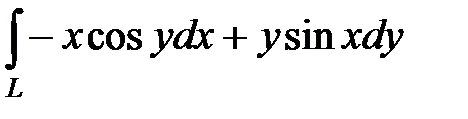 , где L − отрезок прямой от точки О (0; 0) до точки
, где L − отрезок прямой от точки О (0; 0) до точки
А ( 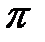 ;
; 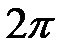 ).
).
6.3. Вычислить криволинейные интегралы второго рода по замкнутым положительно ориентированным контурам L по формуле Грина:
1) 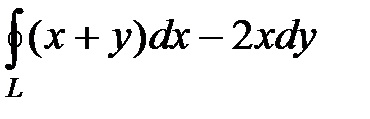 , где L − контур треугольника со сторонами
, где L − контур треугольника со сторонами 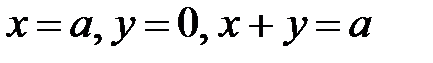 ;
;
2) 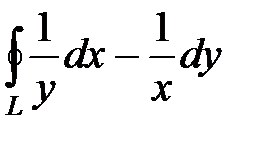 , где L − контур треугольника с вершинами А (1; 1), В (2; 1) и С (2; 2);
, где L − контур треугольника с вершинами А (1; 1), В (2; 1) и С (2; 2);
3) 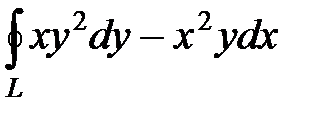 , где L − окружность
, где L − окружность 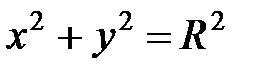 .
.
Приложение
I. Неопределенный интеграл
Основная таблица интегралов
1. 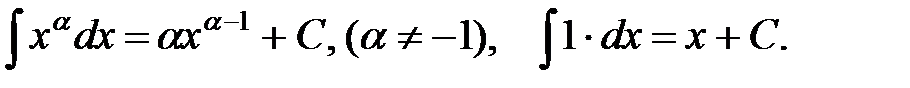
2. 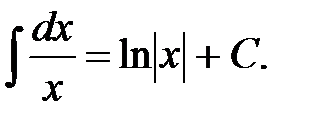
3. 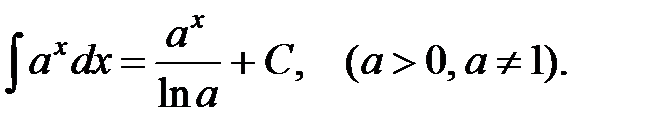
4. 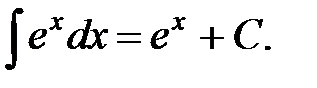
5. 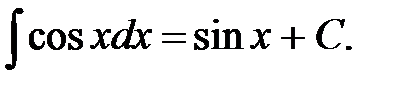
6. 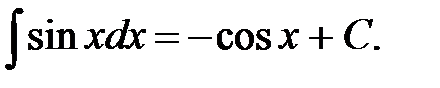
7. 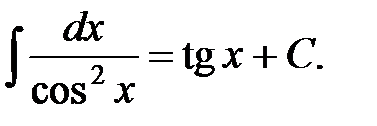
8. 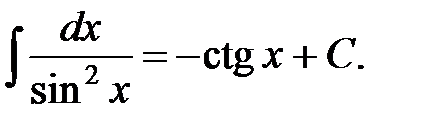
9. 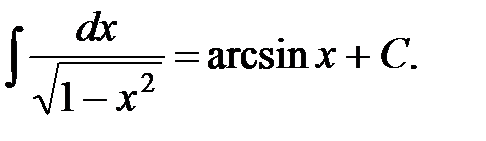
10. 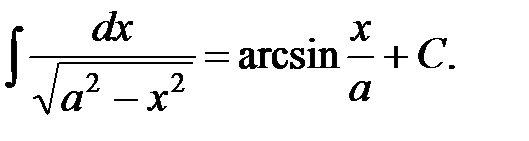
11. 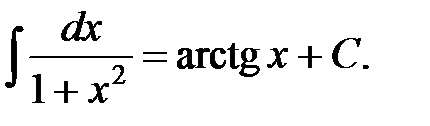
12. 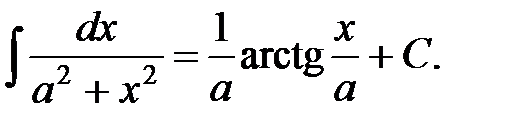
13. 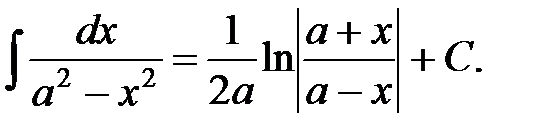
14. 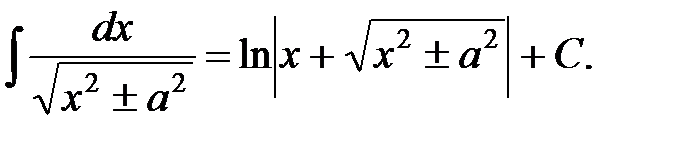
15. 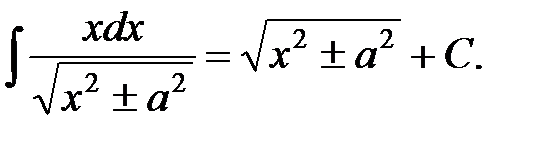
16. 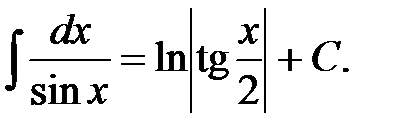
17. 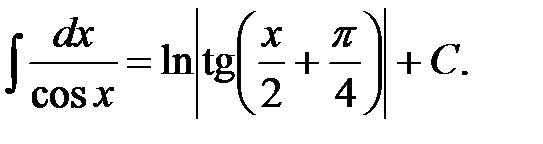
18. 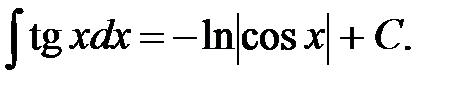
19. 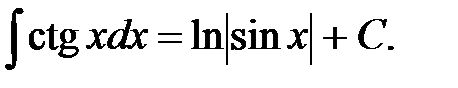
Замена переменной
20. 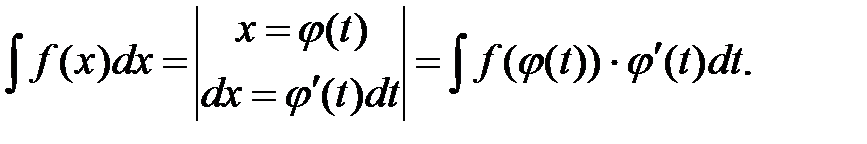
Интегрирование по частям
21. 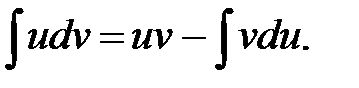
Интегрирование простейших дробей
22. 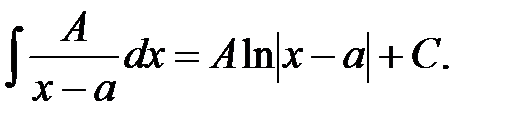
23. 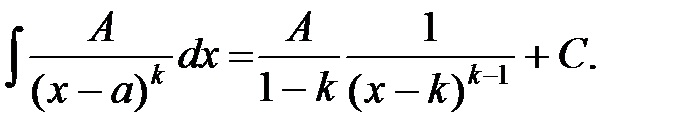
24. 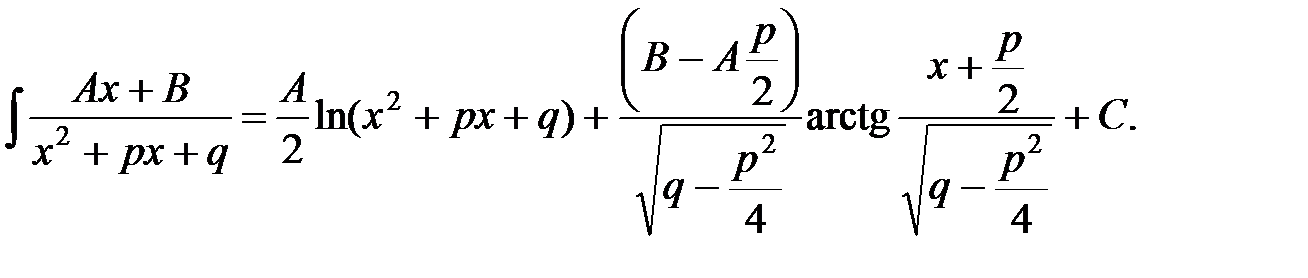
25. 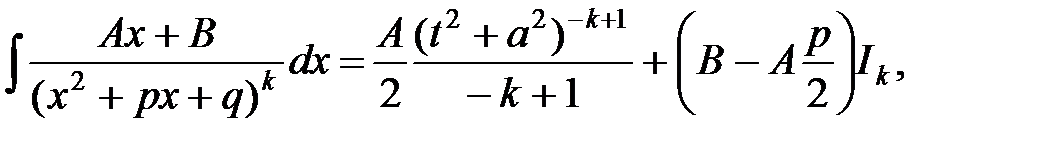 где
где
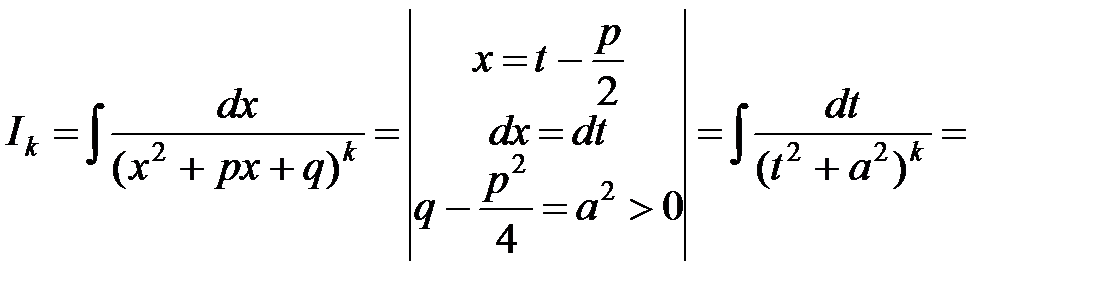
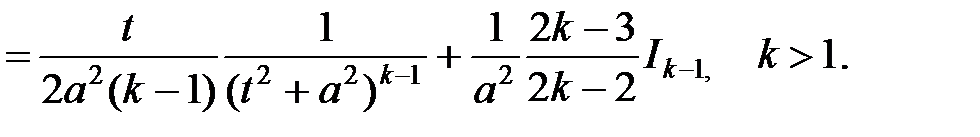
При 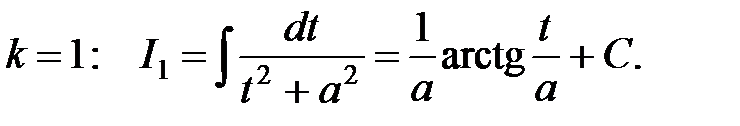
Интегрирование иррациональных функций
| Интеграл | Подстановка |
25. 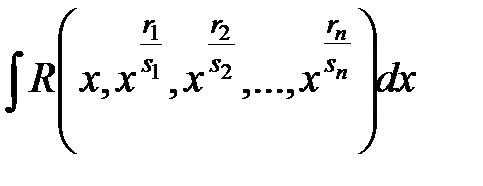
| 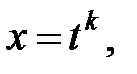 где k − общий знаменатель
дробей
где k − общий знаменатель
дробей 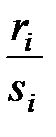 , , 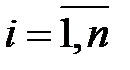 . .
|
26. 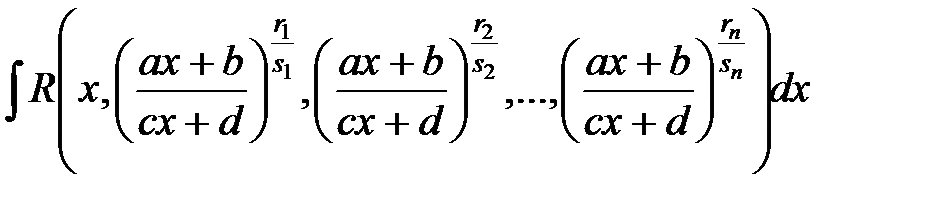
| 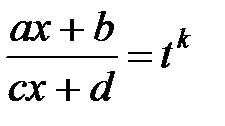 ,
где k − общий знаменатель
дробей ,
где k − общий знаменатель
дробей 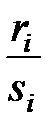 , , 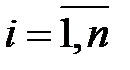 . .
|
Подстановки Эйлера
27. 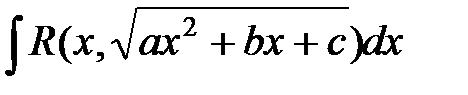
| 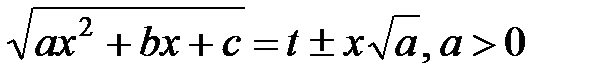 ; ;
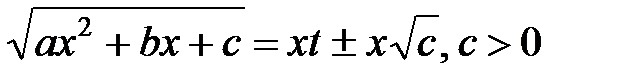 ; ;
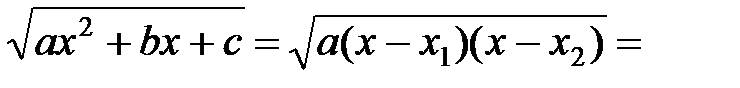
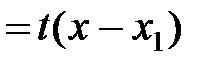
|
Интегрирование тригонометрических функций
28. 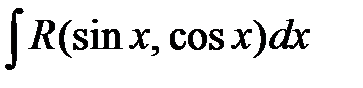
| 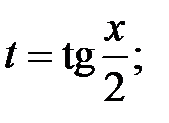
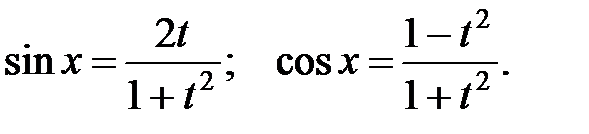
|
29. 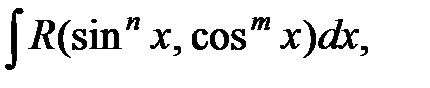 n, m − четные, хотя бы одно из
них отрицательное
n, m − четные, хотя бы одно из
них отрицательное
| 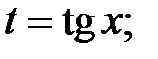
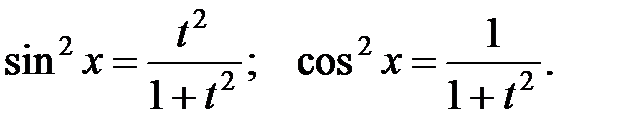
|
30. 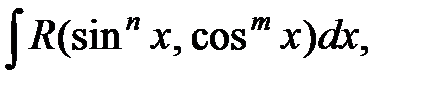
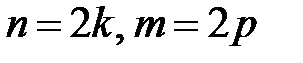
| 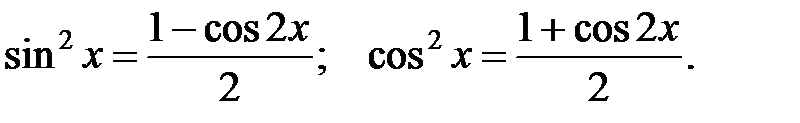
|
31. 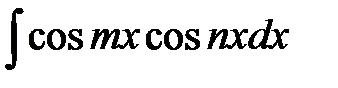
| 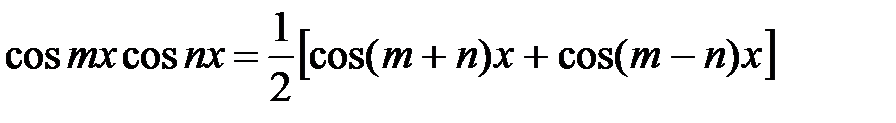
|
32. 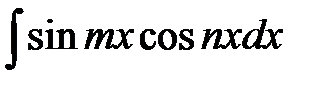
| 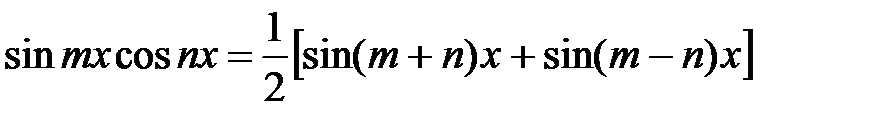
|
33. 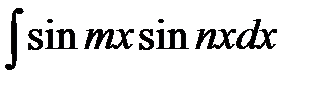
| 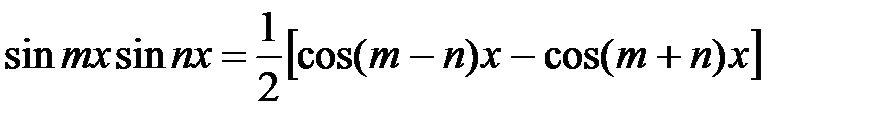
|
Тригонометрические подстановки
34. 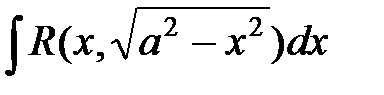
| 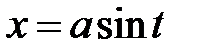 или или 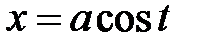
|
35. 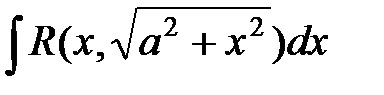
| 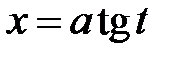 или или 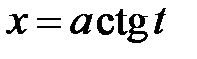
|
36. 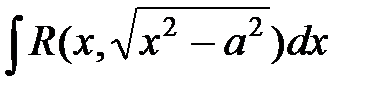
| 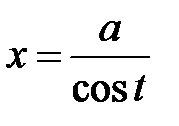 или или 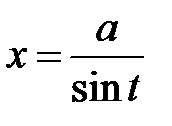
|
II. Определенный интеграл
Формула Ньютона-Лейбница
37. 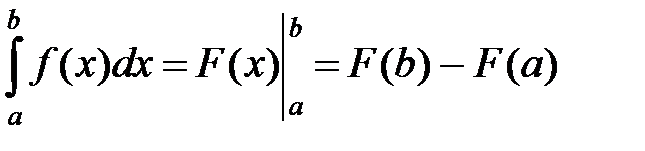 .
.
Замена переменной
38. 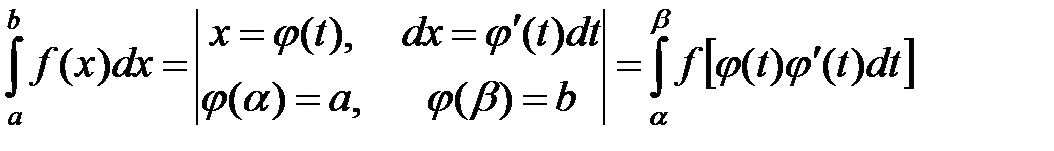 .
.
Интегрирование по частям
39. 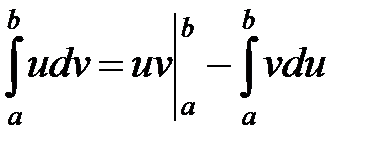 .
.
Дата добавления: 2016-04-14; просмотров: 18123;
