Примеры решения задач. 1. Вычислить площадь фигуры D, ограниченной параболой
1. Вычислить площадь фигуры D, ограниченной параболой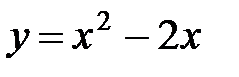 
и прямой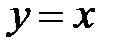 
.
► Построим фигуру D:
| у |
| х |
|
|
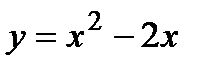
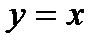
| D |
| Рис. 11 |
Решив систему уравнений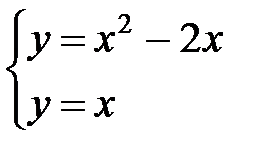 
, получим 
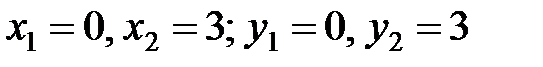соответственно. Следовательно, линии, ограничивающие область D, пересекаются в точках 
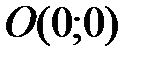и М(3;3).
Область D задается системой неравенств:
D: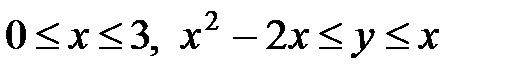 
.
Тогда
◄
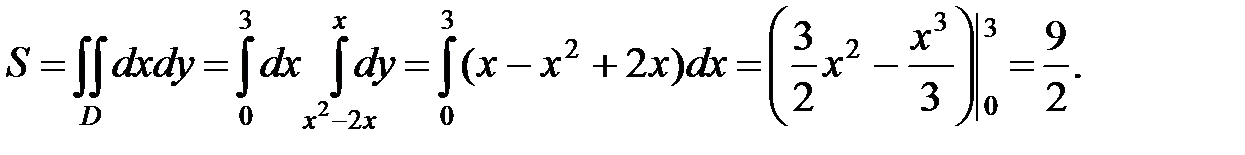2. Найти объем тела Т, ограниченного цилиндрами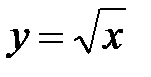 
, 
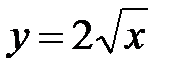и плоскостями 
.
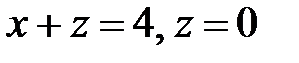► Данное тело Т ограничено сверху плоскостью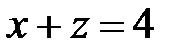 
, снизу плоскостью 
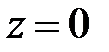, по бокам прямыми цилиндрами 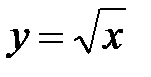и .
И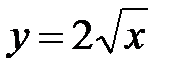зобразим тело Т и область интегрирования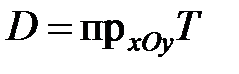 
:
| z |
| y |
| x |
| T |
| A |
| Рис. 12 |
| у |
| х |
|
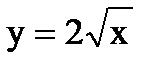
| D |
| Рис. 13 |
Переменная x изменяется от 0 до 4, т.е.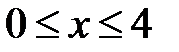 
; при любом значении из этого промежутка 
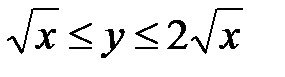. Кроме того, 
.
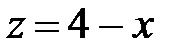Итак,
.◄
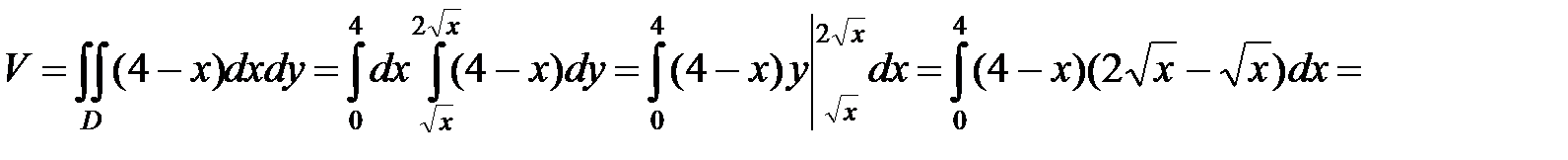
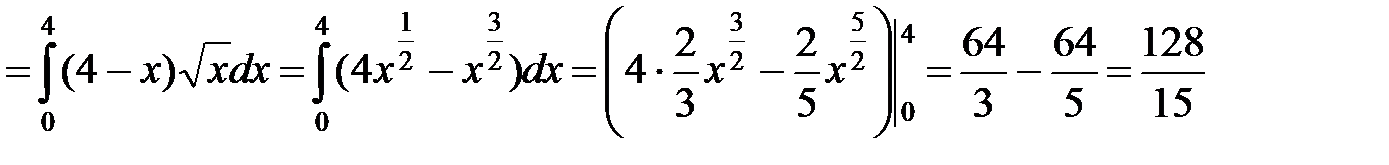3. Найти координаты центра масс однородной пластинки, ограниченной линиями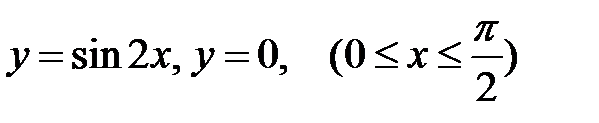 
; плотность 
.
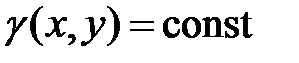► Координаты центра масс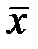 
и 
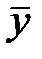плоской фигуры D с плотностью 
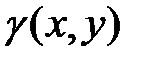вычисляются по формулам:
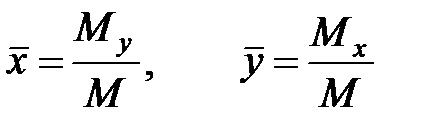, (5.4)
| у |
| х |
|
|
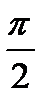
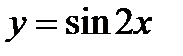
| D |
| Рис. 14 |
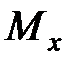и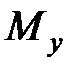 
ее статические моменты относительно осей координат 
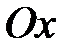и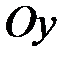 
соответственно. В случае однородной пластинки эти формулы принимают вид
,
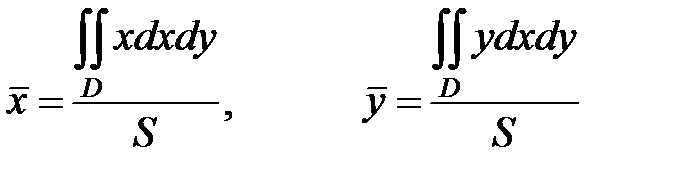где S − площадь области D.
Найдем площадь S пластинки.
.
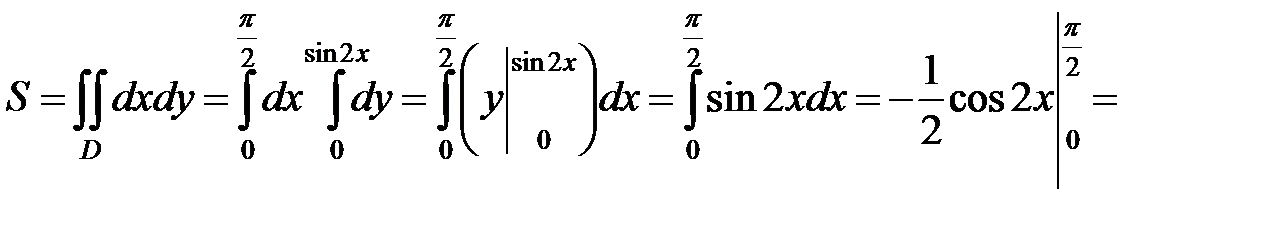
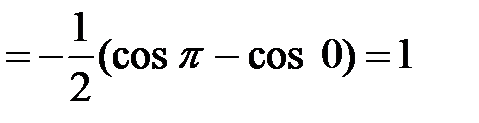Вычислим статические моменты:
.◄
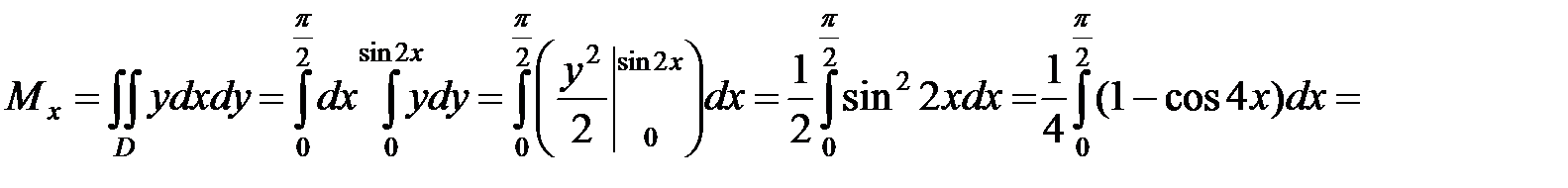
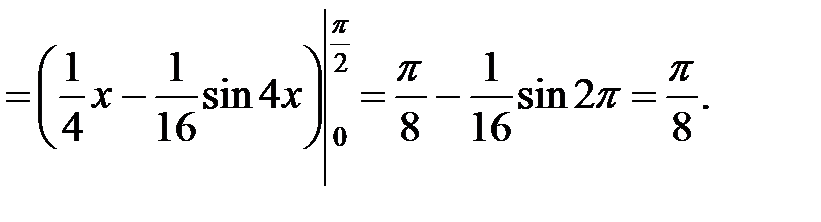
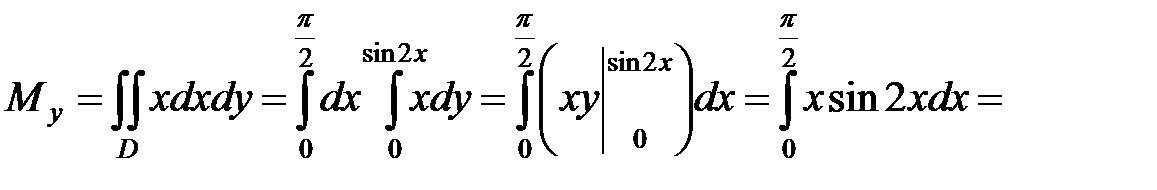
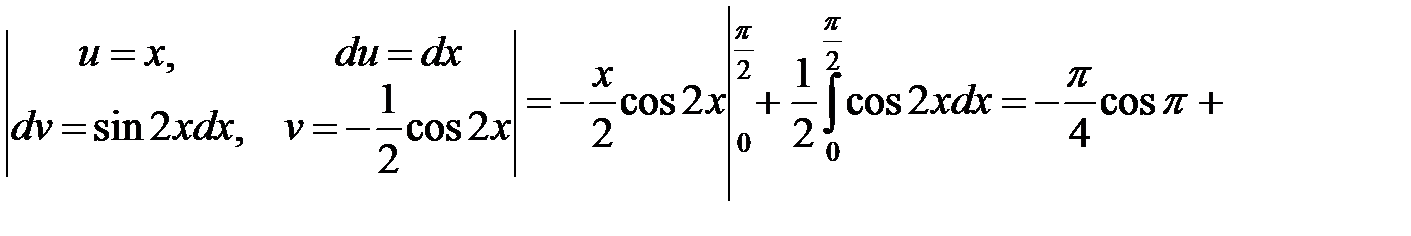
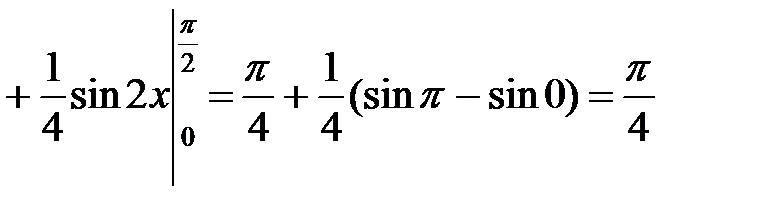Таким образом, центр масс имеет координаты:
◄
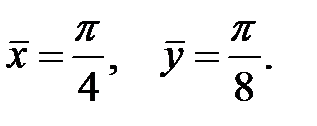4. Найти моменты инерции однородной фигуры (плотность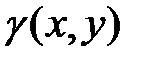 
=const), ограниченной линиями 
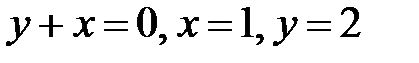, относительно осе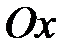й 
и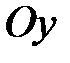 
и начала координат.
► Данная фигура D изображена на рисунке и представляет собой треугольник с вершинами А (1; -1), В (1; 2) и С (-2; 2).
| А |
| х |
| у |
| . |
| С |
| . |
| . |
| D |
| В |
| у=2 |
| х=1 |
| у=-х |
| Рис.15 |
Моменты инерци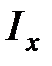и 
и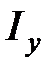 
плоской фигуры с плотностью 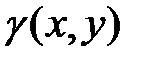относительно осе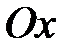й и 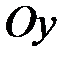вычисляются по формулам:
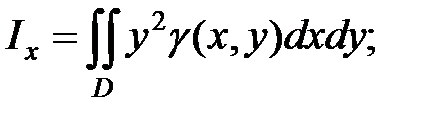
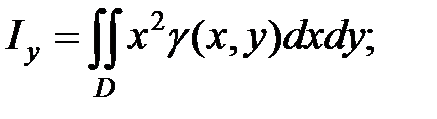(4.5)
;
.
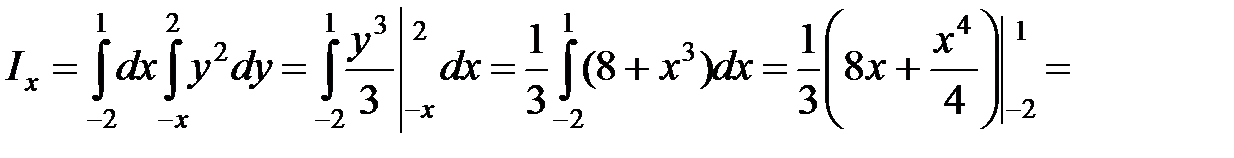
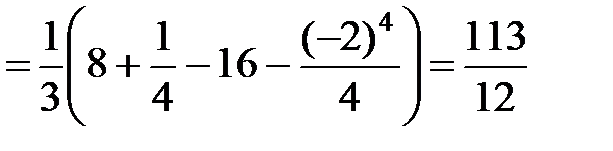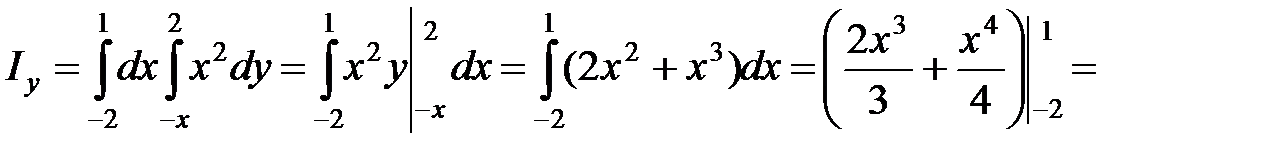
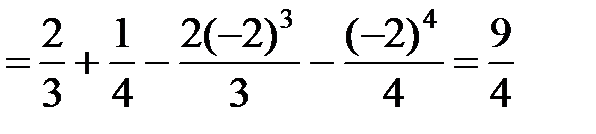Момент инерции относительно начала координат вычисляем по формуле:
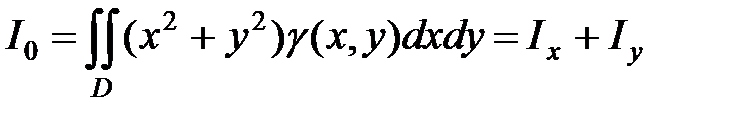, (4.6)
следовательно,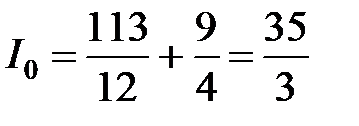 
.◄
5. Найти объем тела, расположенного внутри цилиндра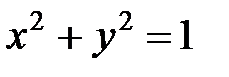 
и ограниченного сферой 
.
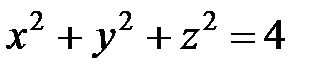► Объем тела выражается тройным интегралом вида
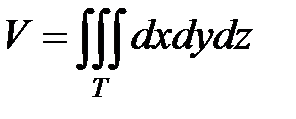. (4.7)
В данном случае вычисления выполним в цилиндрических координатах. Уравнения поверхностей, ограничивающих тело, в цилиндрических координатах имеют следующий вид: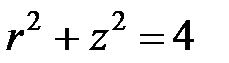 
− уравнение сферы, 
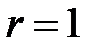− уравнение цилиндра.
Таким образом, объем тела будет выражаться трехкратным интегралом
= 
.◄
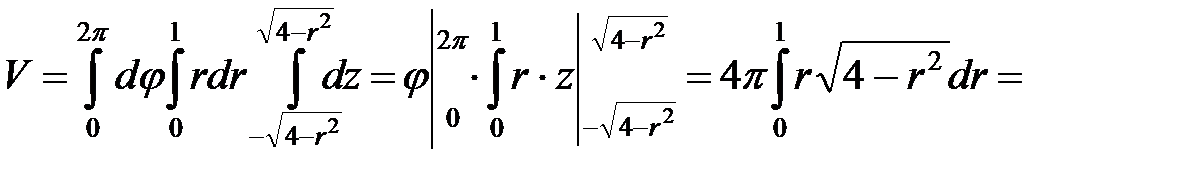
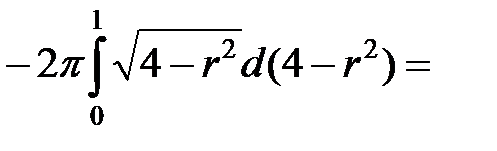
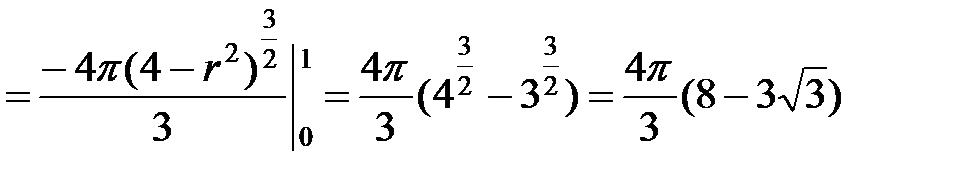Дата добавления: 2016-04-14; просмотров: 1323;