Примеры решения задач. 1. Вычислить интегралы от иррациональных функций:
1. Вычислить интегралы от иррациональных функций:
а) 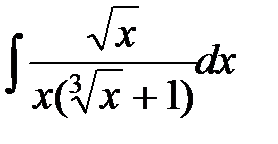 ; б)
; б) 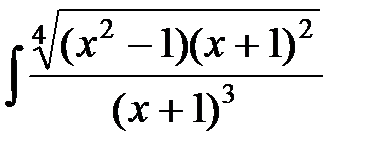 ;
;
в) 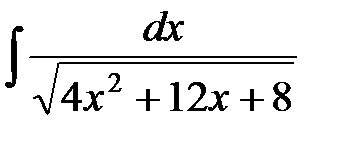 ; г)
; г) 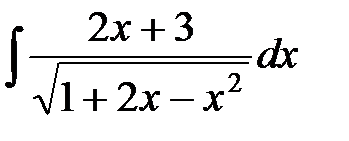 .
.
►а) Подстановкой 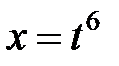 приведем интеграл к рациональному виду. Тогда
приведем интеграл к рациональному виду. Тогда 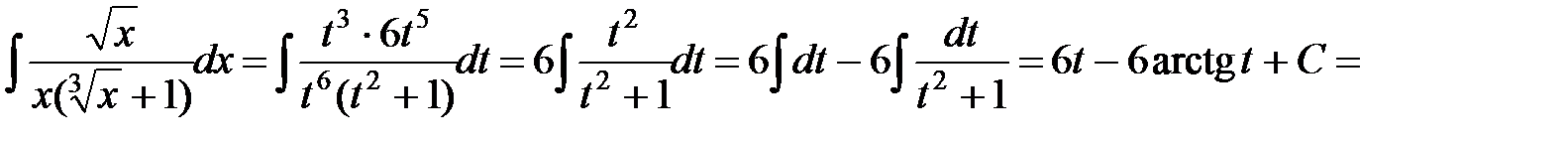
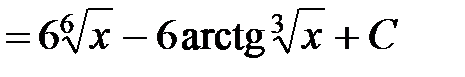 .
.
б) Заметим, что
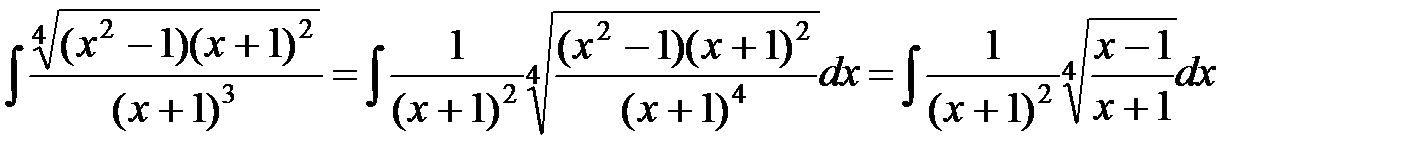 .
.
Применим подстановку 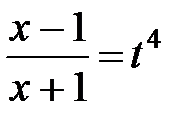 , откуда
, откуда
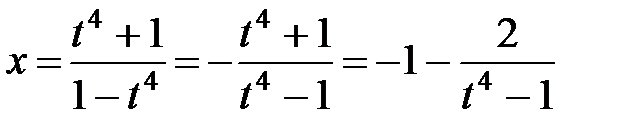 ;
;
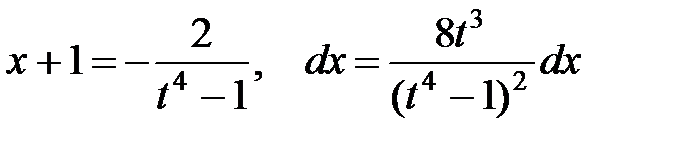 .
.
Итак,
 =
=
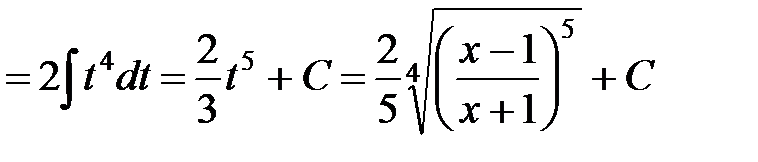 .
.
в) Выделяя полный квадрат в квадратном трехчлене под знаком корня, получаем:
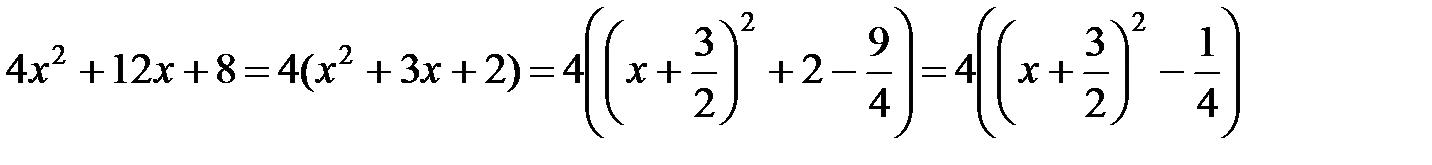 .
.
Тогда, используя табличный интеграл 14, находим
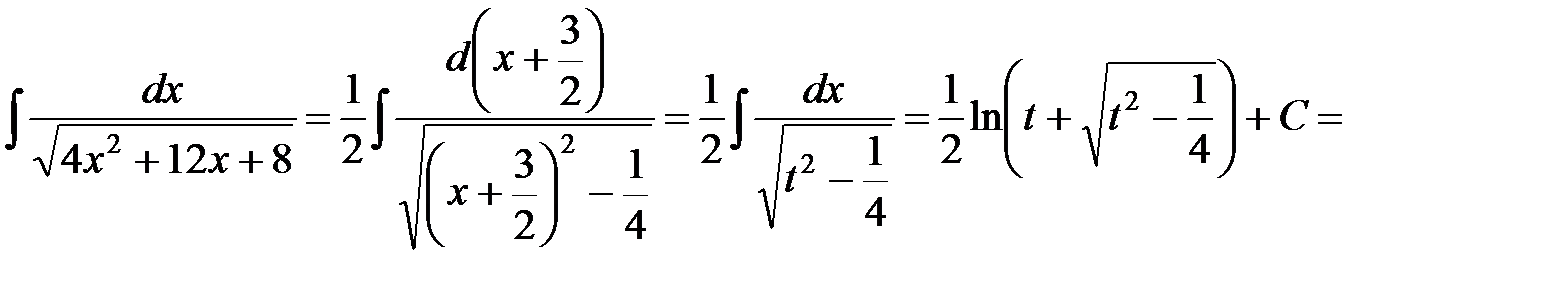
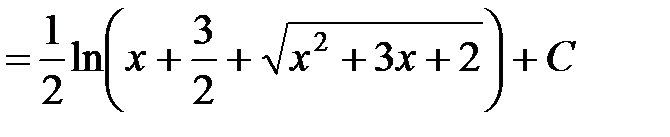 .
.
г) Разобьем данный интеграл на сумму двух интегралов (в первом в числителе образуем производную от подкоренного выражения, а во втором выделим полный квадрат в подкоренном выражении):
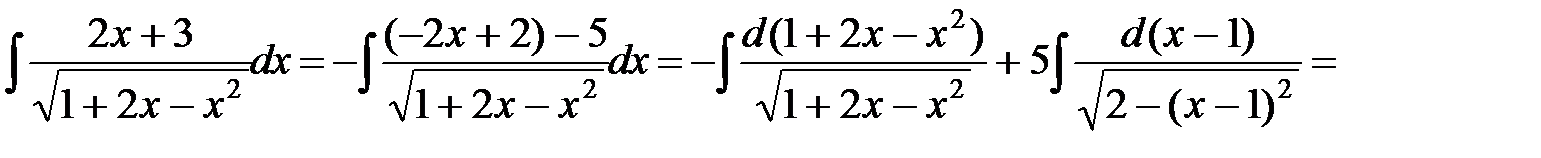
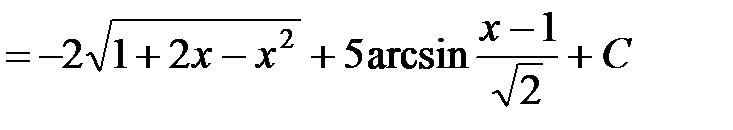 .◄
.◄
Задания для самостоятельной работы
1.6. Найти интегралы от иррациональных функций:
1) 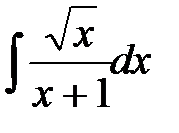 ; 2)
; 2) 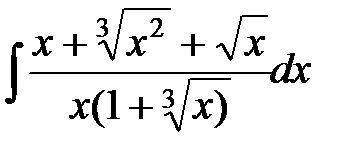 ;
;
3) 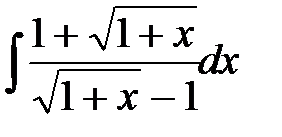 ; 4)
; 4) 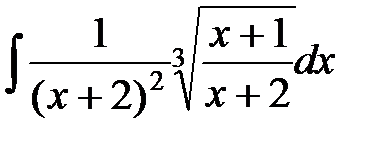 ;
;
5) 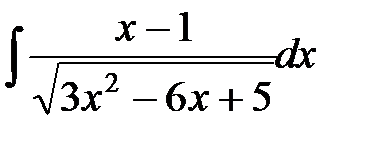 ; 6)
; 6) 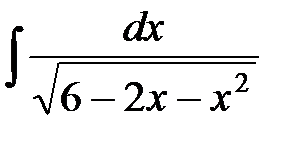 ;
;
7) 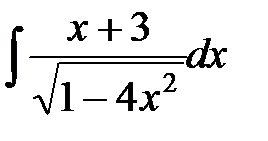 ; 8)
; 8) 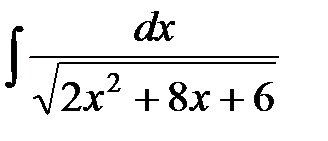 ;
;
9) 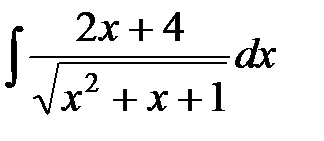 ; 10)
; 10) 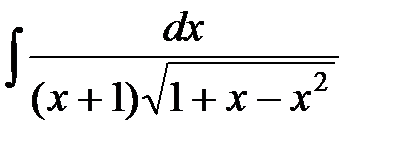 ;
;
11) 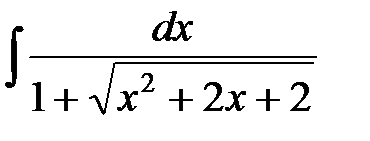 ; 12)
; 12) 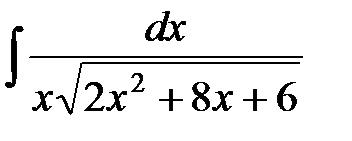 .
.
Тема 2. Определенный интеграл.
Формула Ньютона-Лейбница.
Вычисление определенных интегралов
Примеры решения задач
.
1. Вычислить определенные интегралы, используя их свойства и формулу Ньютона-Лейбница:
а) 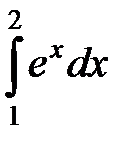 ; б)
; б) 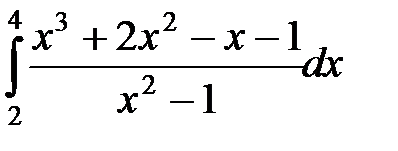 ; в)
; в) 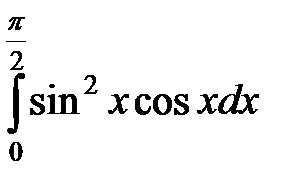 .
.
►Так как все подынтегральные функции непрерывны на соответствующих отрезках, то получаем:
а) 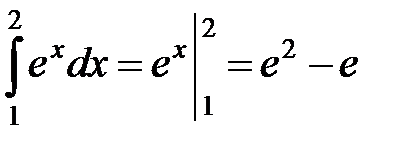 ;
;
б) Под знаком интеграла неправильная дробь. Выделим целую часть, используя разложение
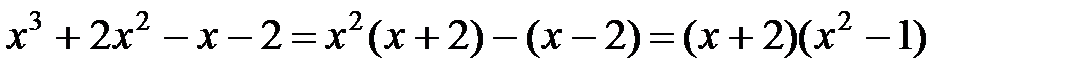 .
.
Имеем:
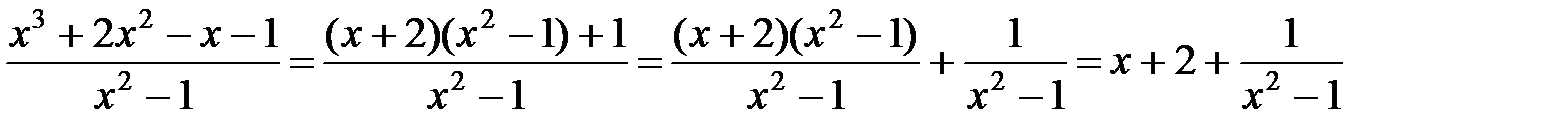 ,
,
и данный интеграл
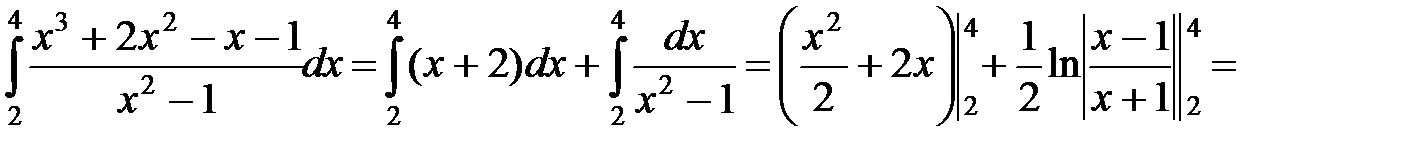
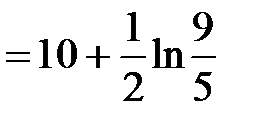 ;
;
в) 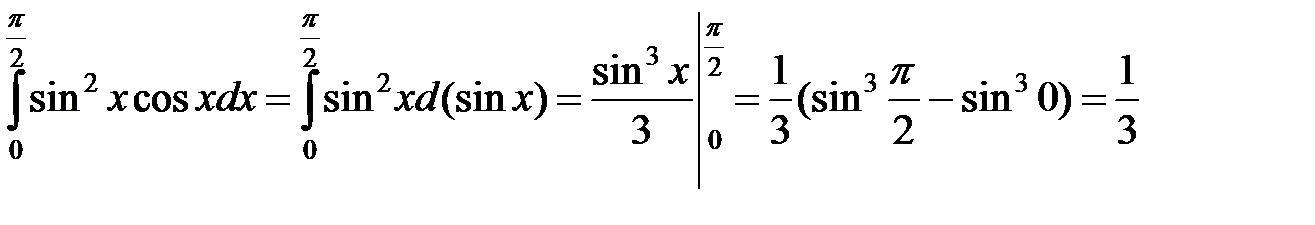 .◄
.◄
2. Методом замены переменной вычислить определенные интегралы:
а) 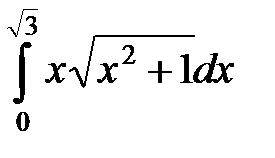 ; б)
; б) 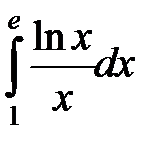 ; в)
; в) 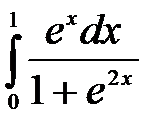 .
.
а) Введем новую переменную 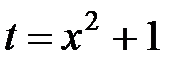 . Тогда
. Тогда 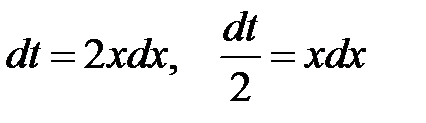 и новые пределы интегрирования
и новые пределы интегрирования 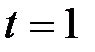 при
при 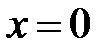 и
и 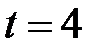 при
при 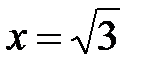 .
.
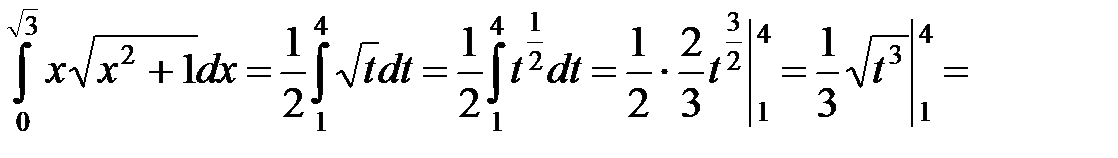
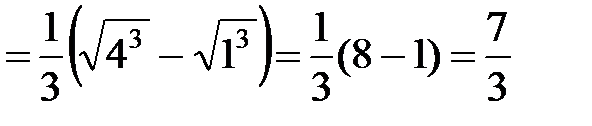 ;
;
б) 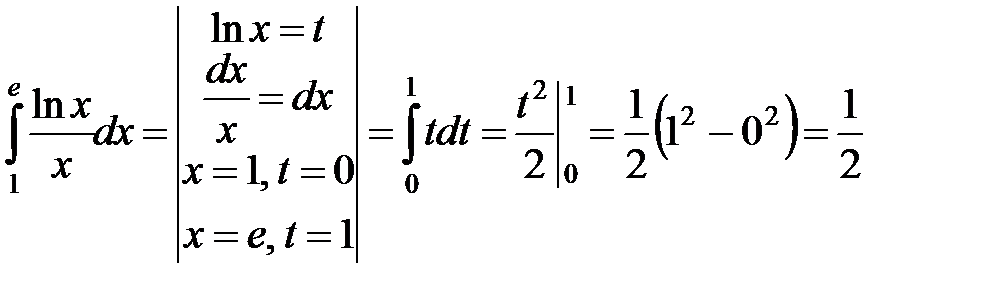 ;
;
в) 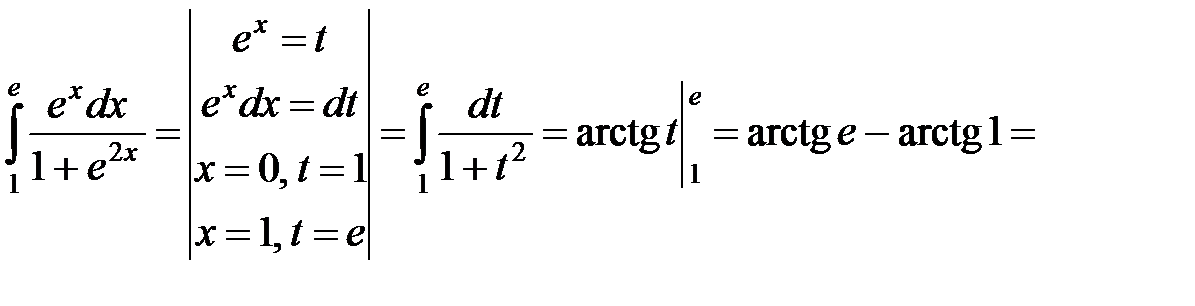
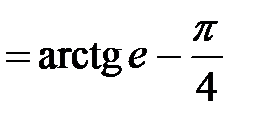 .◄
.◄
3. Используя формулу интегрирования по частям (1.4), вычислить следующие интегралы:
а) 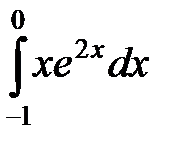 ; б)
; б) 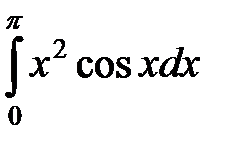 .
.
►а) 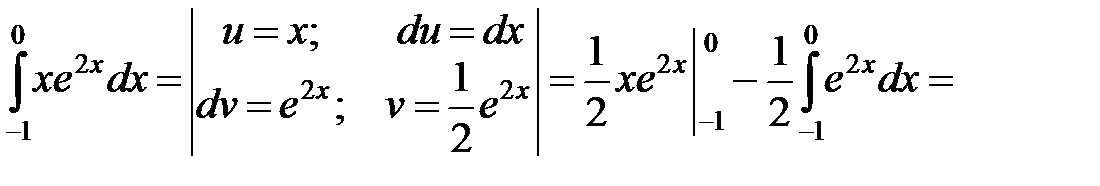
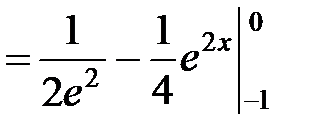
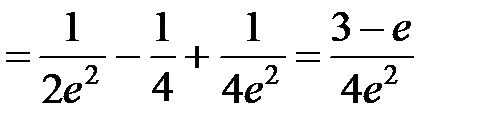 .
.
б) 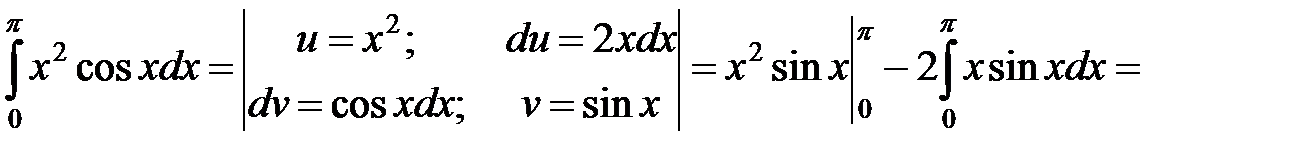
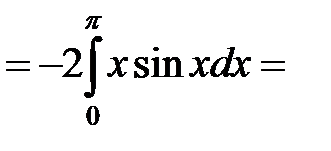
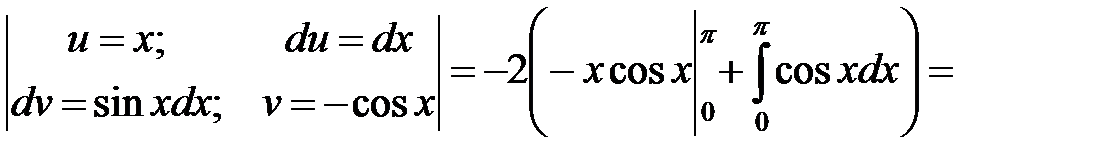
= 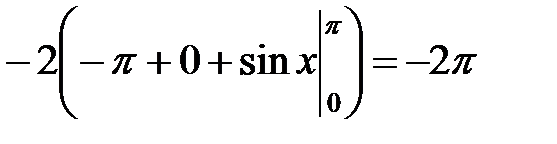 .◄
.◄
4. Вычислить интеграл 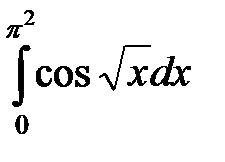 .
.
►Используем подстановку 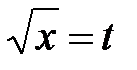 . Тогда
. Тогда 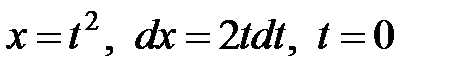 при
при 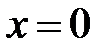 ,
, 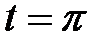 при
при 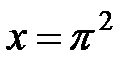 и
и 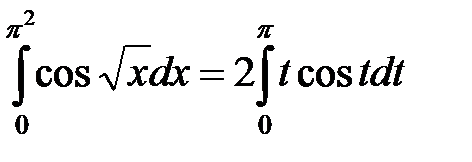 .
.
К последнему интегралу применим интегрирование по частям:
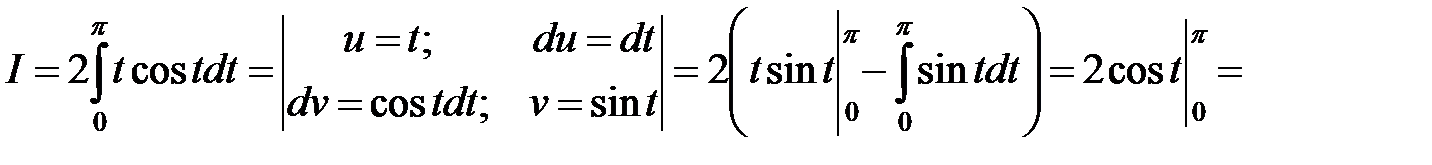
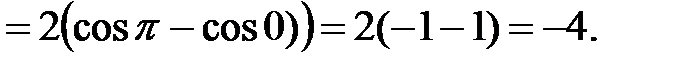 ◄
◄
Дата добавления: 2016-04-14; просмотров: 1306;
