Примеры решения задач. Неопределенный интеграл
Неопределенный интеграл
Непосредственное интегрирование.
Замена переменной. Интегрирование по частям.
Примеры решения задач
1. Вычислить интегралы:
а) 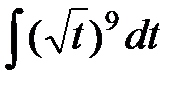 ; б)
; б) 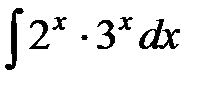 ; в)
; в) 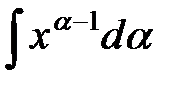 ;
;
г) 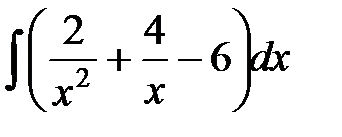 ; д)
; д) 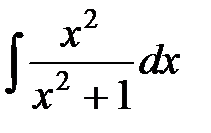 ; е)
; е) 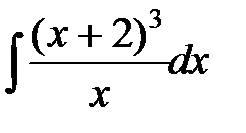 ;
;
ж) 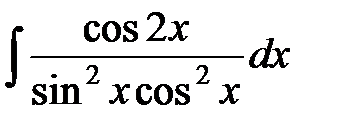 ; з)
; з) 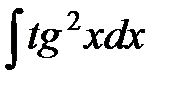 .
.
►а) Применив табличный интеграл 1 (см. приложение), получим:
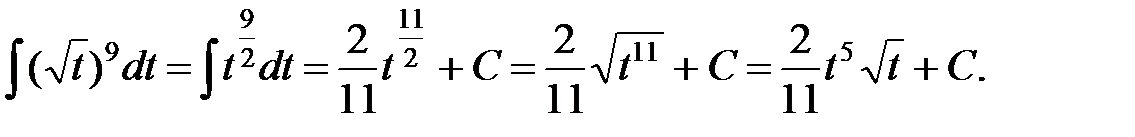
б) По табличному интегралу 3, при 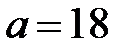 имеем:
имеем:
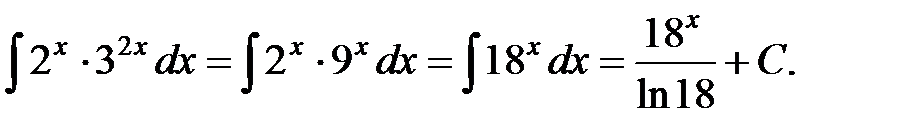
в) В данном случае переменной интегрирования является 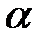 , а переменную
, а переменную 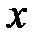 считаем постоянной, причем
считаем постоянной, причем 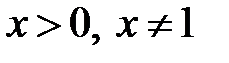 . Тогда, по свойствам неопределенного интеграла и табличному интегралу 3 имеем:
. Тогда, по свойствам неопределенного интеграла и табличному интегралу 3 имеем:
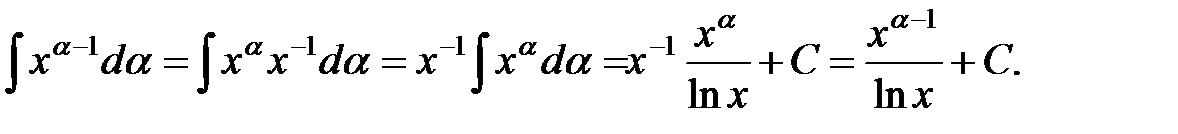
г) Аналогично предыдущему находим:
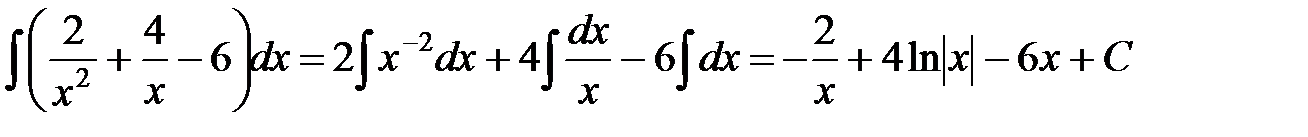 .
.
д) В числителе дроби прибавим и отнимем 1, затем почленно поделим числитель на знаменатель и применим табличные интегралы 1 и 11:
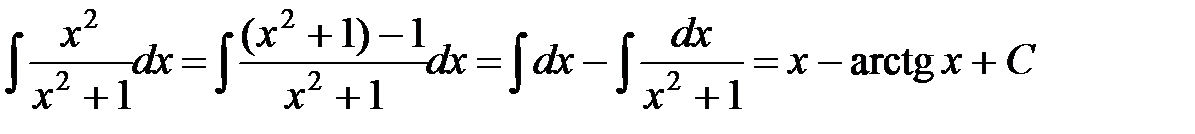 .
.
е) 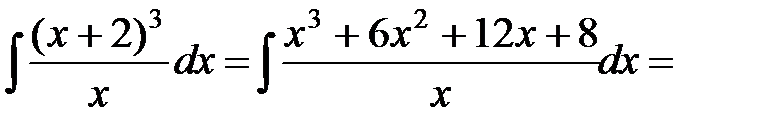
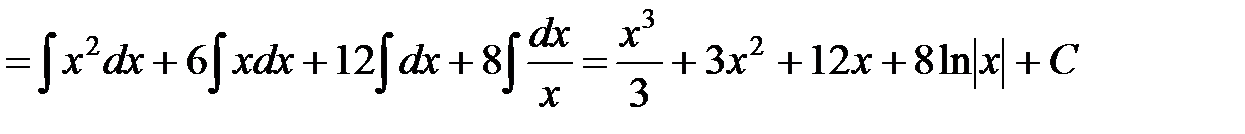 .
.
ж) Подынтегральное выражение запишем в виде:
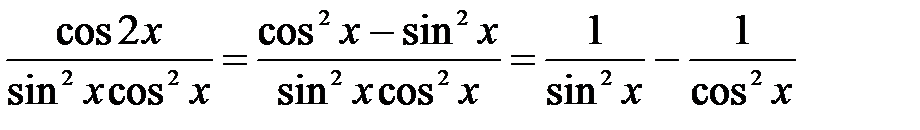 .
.
Согласно табличным интегралам 8 и 7 имеем:
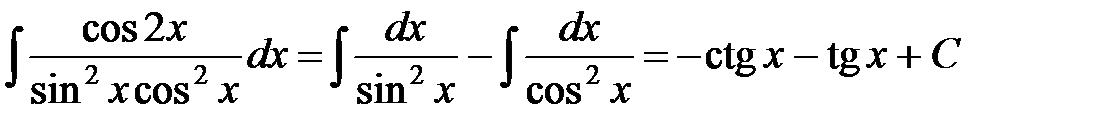 .◄
.◄
2. Вычислить интегралы методом подстановки:
а) 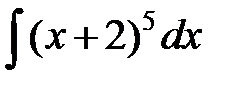 ; б)
; б) 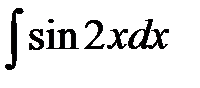 ; в)
; в) 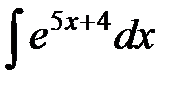 ;
;
г) 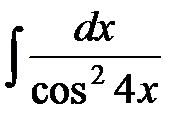 ; д)
; д) 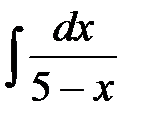 ; е)
; е) 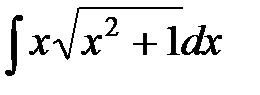 ;
;
ж) 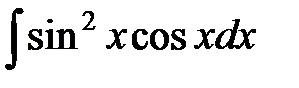 ; з)
; з) 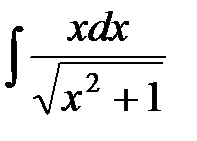 ; и)
; и) 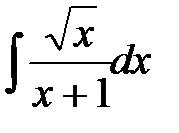 .
.
►а) Пусть 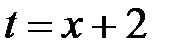 , тогда
, тогда 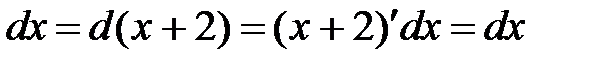 . Подставим эти значения в подынтегральное выражение:
. Подставим эти значения в подынтегральное выражение:
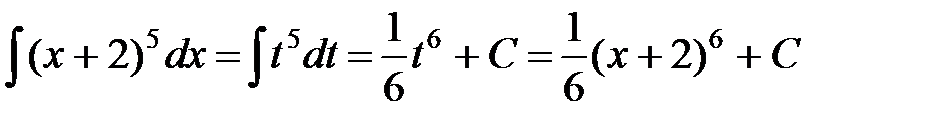 .
.
Данный интеграл можно вычислить следующим способом:
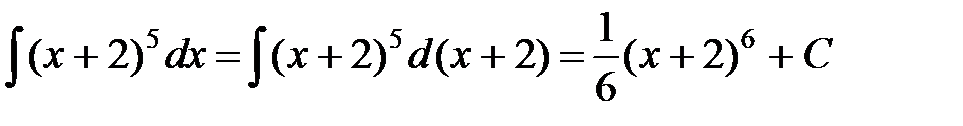 .
.
б) Аналогично предыдущему примеру имеем:
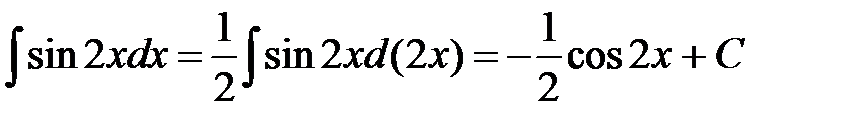 .
.
в) Пусть 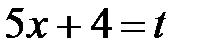 , тогда
, тогда 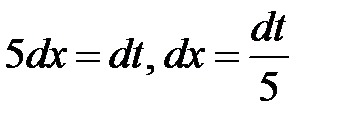 , и
, и
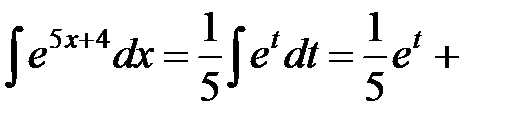
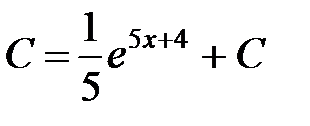 .
.
г) 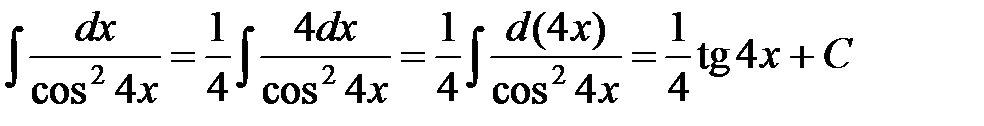 .
.
Рассмотренные выше интегралы легко вычислить по общей формуле
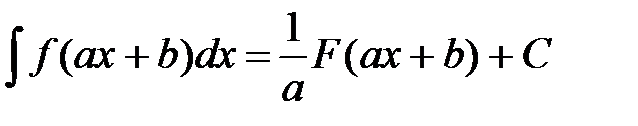 , (1.1)
, (1.1)
где 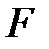 − первообразная функции
− первообразная функции 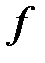 .
.
д) Данный интеграл приводится к табличному, если положить 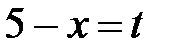 . Тогда
. Тогда 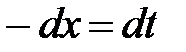 и
и 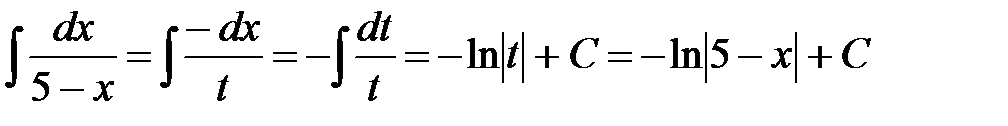 .
.
Приведем еще одну общую формулу:
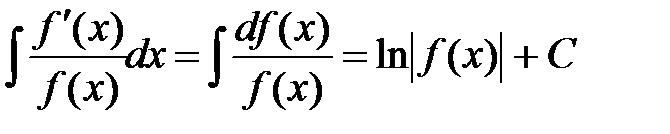 (1.2)
(1.2)
е) Так как 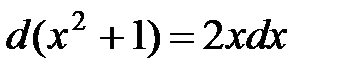 , то, умножив и поделив интеграл на 2 и внеся множитель 2 под знак интеграла, а затем под знак дифференциала, получим:
, то, умножив и поделив интеграл на 2 и внеся множитель 2 под знак интеграла, а затем под знак дифференциала, получим:
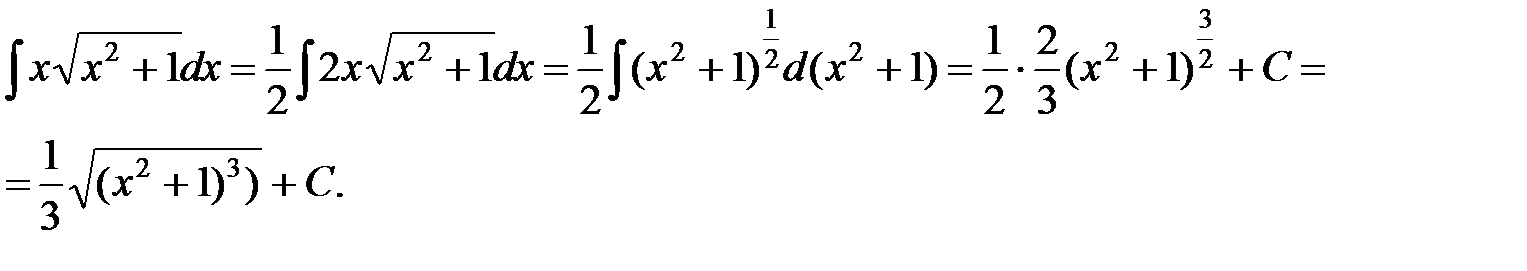
ж) Пусть 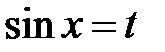 , поскольку
, поскольку 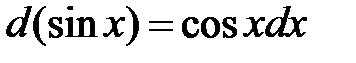 . Имеем
. Имеем
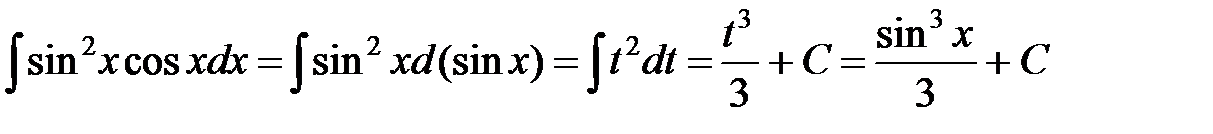 .
.
з) Если числитель подынтегрального выражения умножить на 2, то он будет равен производной подкоренного выражения. Тогда
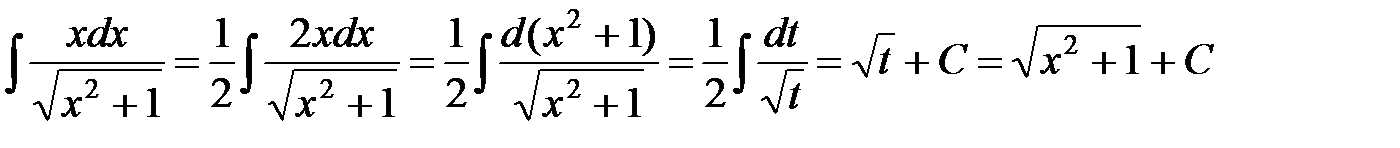 .
.
Полезно запомнить общую формулу, которая фактически применялась при вычислении данного интеграла, а именно
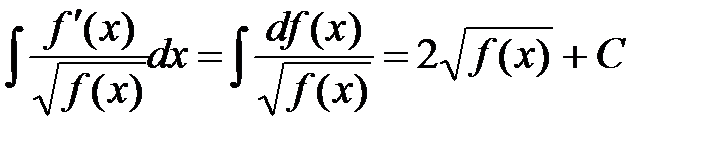 (1.3)
(1.3)
и) Пусть 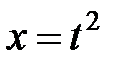 . Тогда
. Тогда 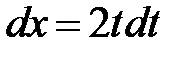 и
и
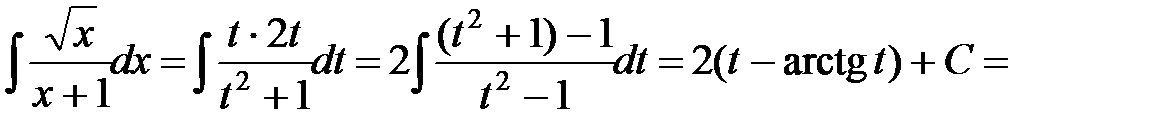
= 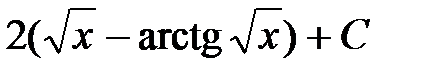 .◄
.◄
3. Вычислить интегралы методом интегрирования по частям:
а) 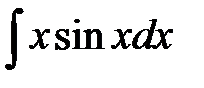 ; б)
; б) 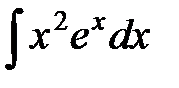 ; в)
; в) 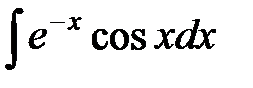 ;
;
г) 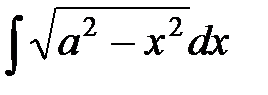 ; д)
; д) 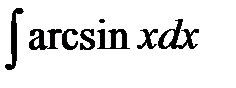 .
.
► Для применения метода интегрирования по частям необходимо подынтегральное выражение представить в виде произведения двух множителей 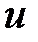 и
и 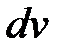 , причем через
, причем через 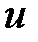 обозначить функцию, которая упрощается при дифференцировании (например,
обозначить функцию, которая упрощается при дифференцировании (например, 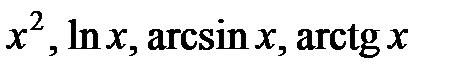 ), а через
), а через 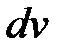 − выражение, из которого непосредственным интегрированием несложно определить
− выражение, из которого непосредственным интегрированием несложно определить 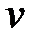 (например,
(например, 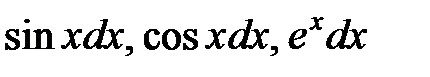 ).
).
а) Пусть 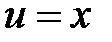 ,
, 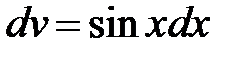 , тогда
, тогда 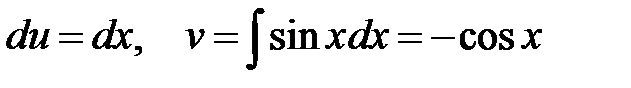 .
.
Подставляя эти значения в формулу интегрирования по частям
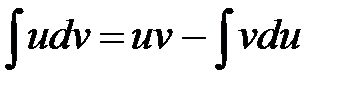 (1.4)
(1.4)
получим:
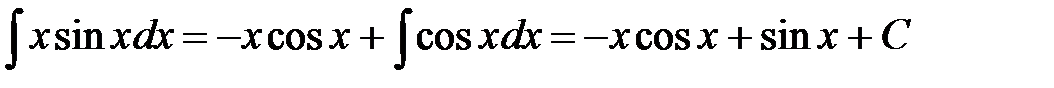 .
.
б) Пусть 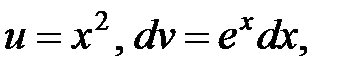 тогда
тогда 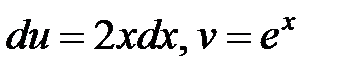 . Тогда
. Тогда
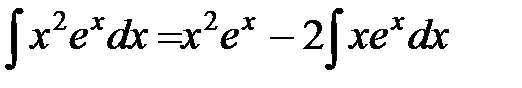 .
.
К последнему интегралу снова применим метод интегрирования по частям, полагая 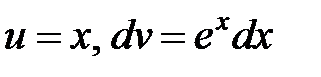 , откуда
, откуда 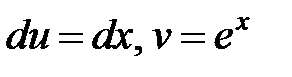 . Итак, имеем
. Итак, имеем 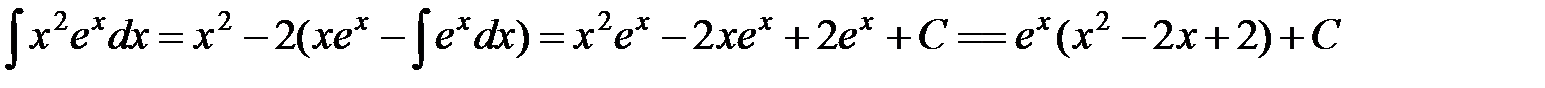 .
.
в) Пусть 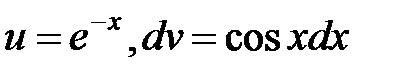 , тогда
, тогда 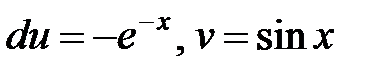 . Имеем:
. Имеем:
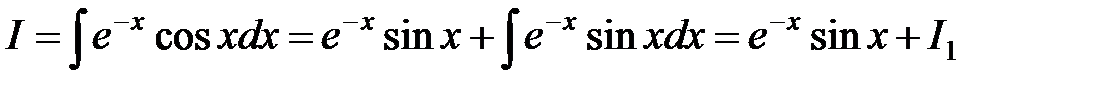 . (1.5)
. (1.5)
Применим формулу интегрирования по частям к интегралу 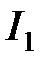 , полагая
, полагая 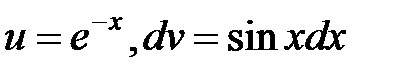 , откуда
, откуда 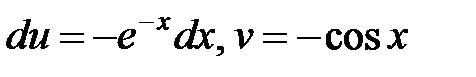 . Тогда
. Тогда
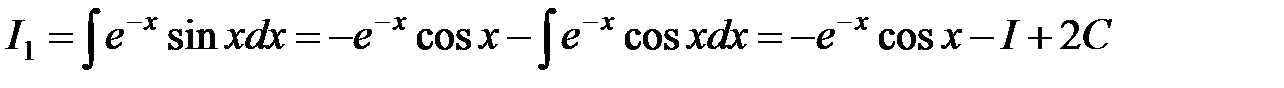 .
.
Подставляя этот результат в (1.5), получаем уравнение с неизвестным интегралом 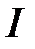 , т.е.
, т.е. 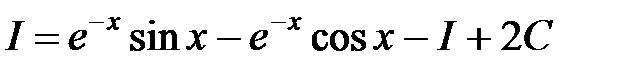 , отсюда
, отсюда
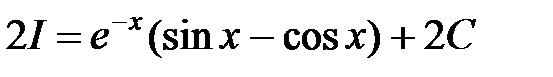 ,
,
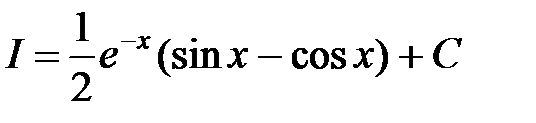 .
.
г) Пусть 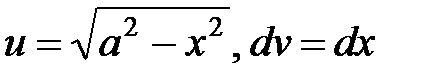 . Тогда
. Тогда 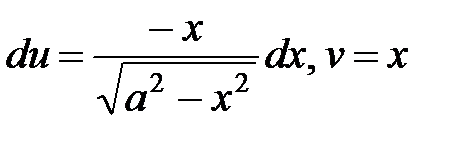 и
и
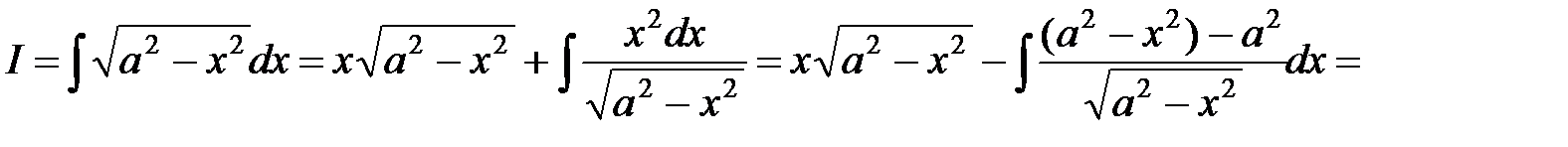
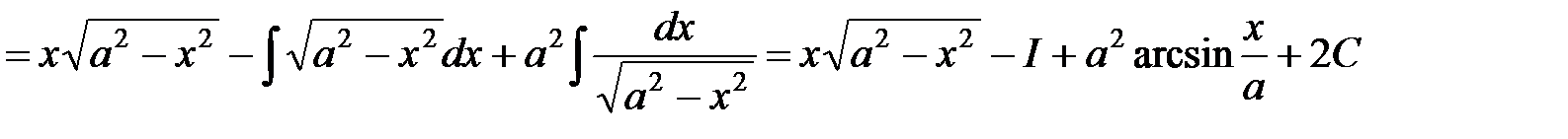 .
.
Аналогично предыдущему примеру
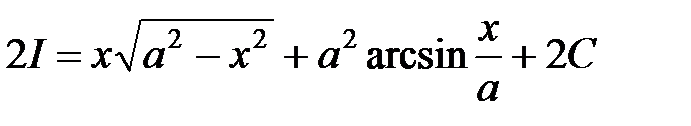 ,
,
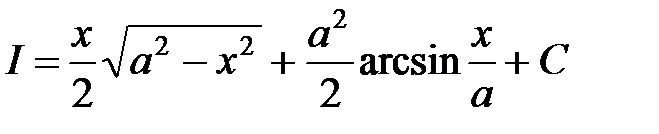 .
.
д) Пусть 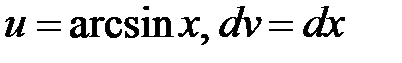 . Тогда
. Тогда 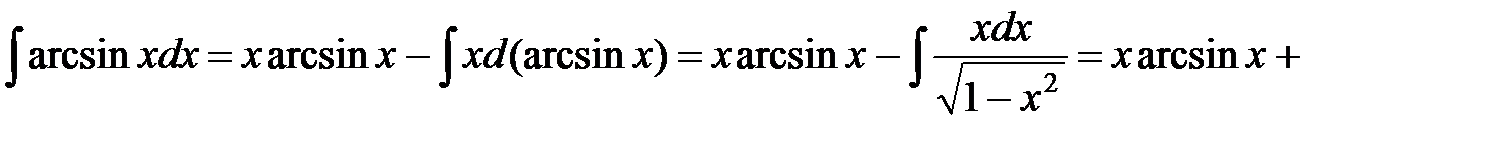
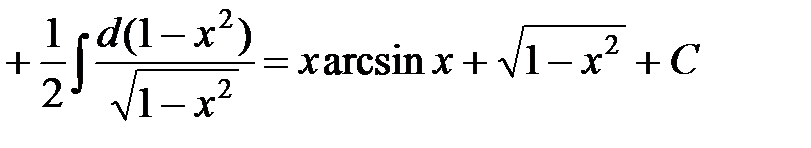 .◄
.◄
Дата добавления: 2016-04-14; просмотров: 999;
