Примеры решения задач. 1. Вычислить интегралы от рациональных функций:
1. Вычислить интегралы от рациональных функций:
а) 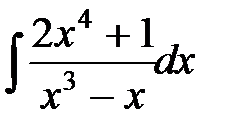 ; б)
; б) 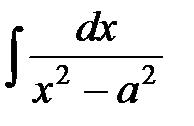 ; в)
; в) 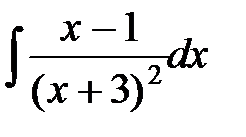 ;
;
г) 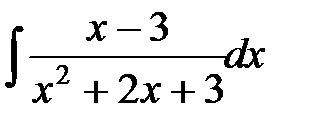 ; д)
; д) 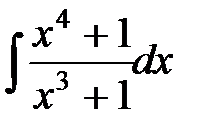 ; е)
; е) 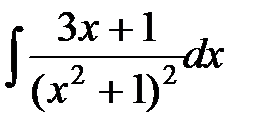 .
.
►а) Выделим целую часть подынтегральной дроби:
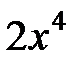 +1 +1
| 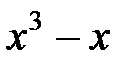
| |
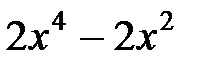
| 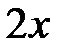
| |
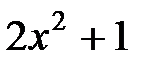
|
Тогда 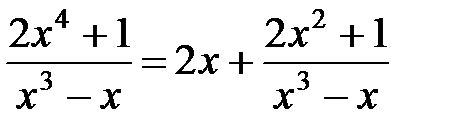 .
.
Разложим знаменатель на множители:
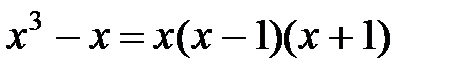
Представим дробь 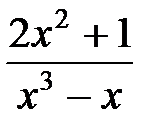 в виде суммы элементарных дробей:
в виде суммы элементарных дробей:
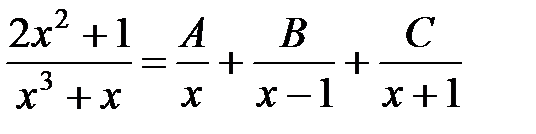 .
.
Правую часть последнего равенства приведем к общему знаменателю и приравняем числители:
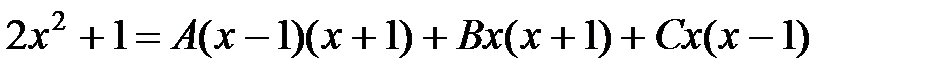 .
.
Поскольку числа 0, 1, 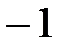 являются корнями знаменателя, то коэффициенты А, В и С удобно вычислить, подставляя именно эти значения
являются корнями знаменателя, то коэффициенты А, В и С удобно вычислить, подставляя именно эти значения 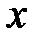 в последнее равенство.
в последнее равенство.
При 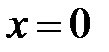
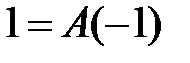 , т.е.
, т.е. 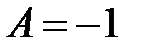 ;
;
при 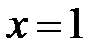
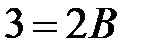 , т.е.
, т.е. 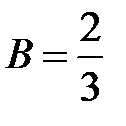 ;
;
при 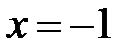
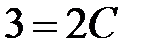 , т.е.
, т.е. 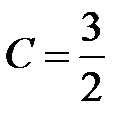 .
.
Вычислим данный интеграл, учитывая значения найденных коэффициентов и предыдущее разложение:
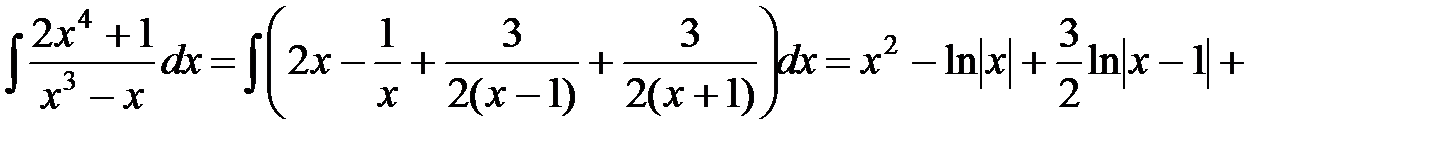
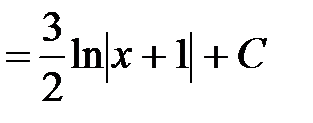 .
.
б) Имеем 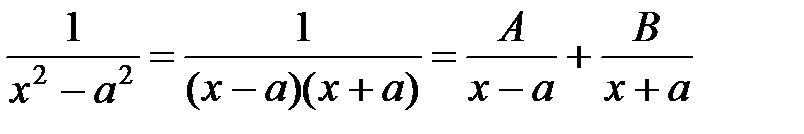 .
.
Аналогично предыдущему примеру получаем табличный интеграл 13:
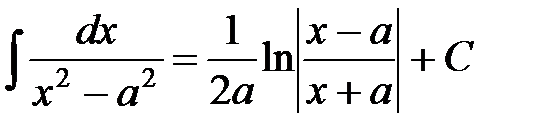 .
.
в) Дробь правильная. Знаменатель имеет двукратный корень – 3. Тогда дробь представима в виде 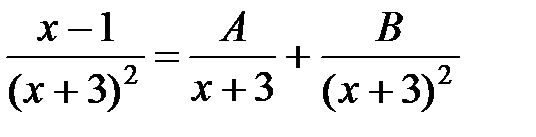 .
.
Приведем к общему знаменателю это равенство и приравняем числители:
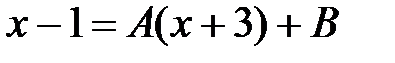 . При
. При 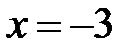 имеем
имеем 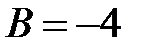 , при
, при 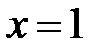 получаем
получаем 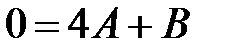 , откуда
, откуда 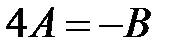 ,
, 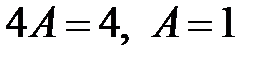 . Подставляя значения А и В в предыдущее разложение, находим:
. Подставляя значения А и В в предыдущее разложение, находим:
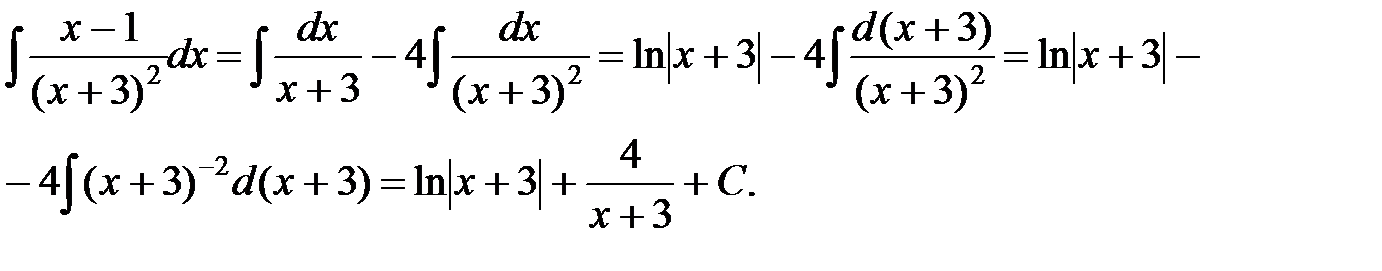
г) Имеем интеграл вида 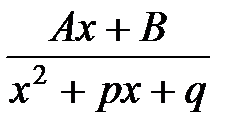 .
.
Выделяя в числителе производную знаменателя и представляя интеграл в виде суммы двух интегралов, к которым последовательно применяем формулу (1.2) и табличный интеграл (12), будем иметь:
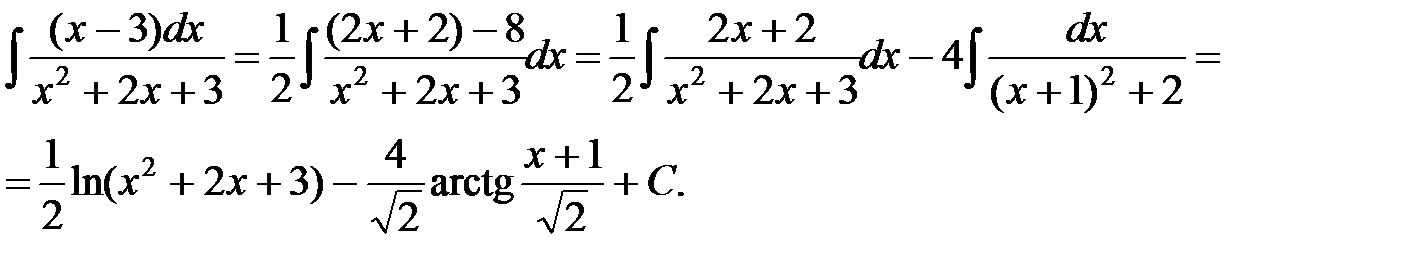
Указанным методом можно вычислить интегралы вида 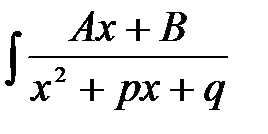 и в случае, если знаменатель имеет действительные корни
и в случае, если знаменатель имеет действительные корни 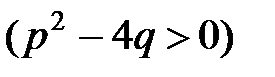 . Тогда вместо формулы 12 таблицы интегралов используют формулу (13).
. Тогда вместо формулы 12 таблицы интегралов используют формулу (13).
д) Знаменатель дроби имеет один действительный корень 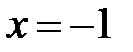 и два мнимых, т.к.
и два мнимых, т.к. 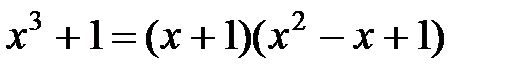 .
.
Выделив целую часть 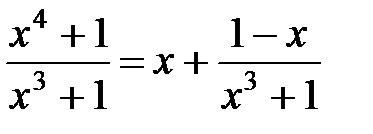 , разложим последнюю дробь на элементарные:
, разложим последнюю дробь на элементарные: 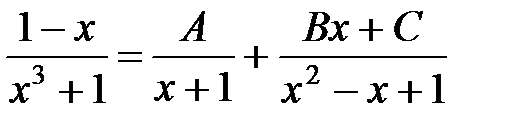 .
.
Коэффициенты А, В и С определяем из равенства 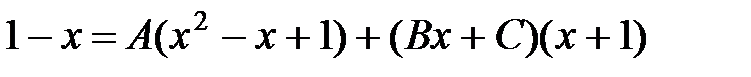 комбинированным способом. При
комбинированным способом. При 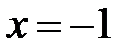 имеем
имеем 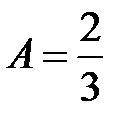 . Для вычисления В и С приравняем коэффициенты при одинаковых степенях:
. Для вычисления В и С приравняем коэффициенты при одинаковых степенях:
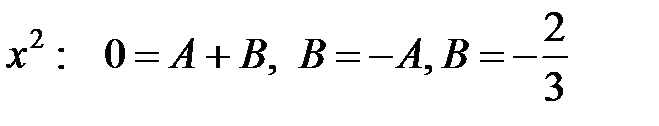 ;
;
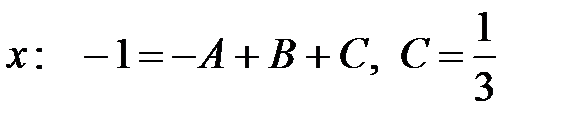 .
.
Тогда
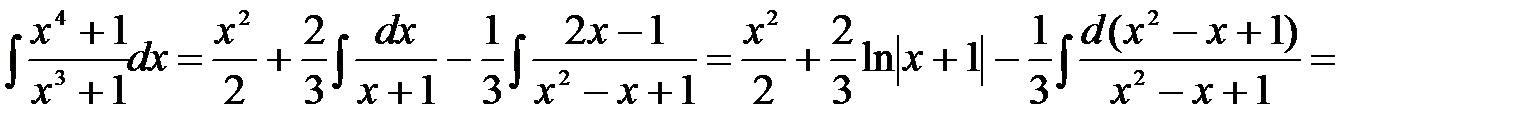
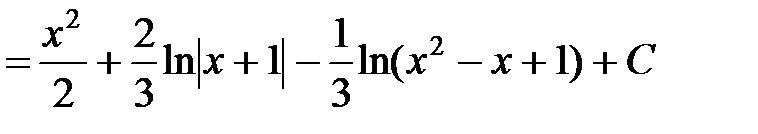 .
.
е) Подынтегральная функция – элементарная дробь вида
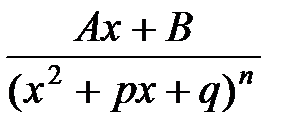 .
.
Имеем 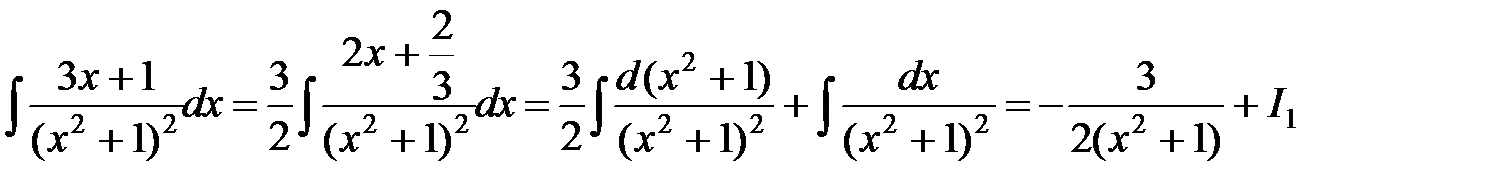 .
.
Последний интеграл вычисляем по формуле 25 (см. приложение) при 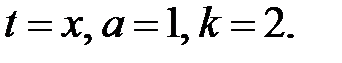
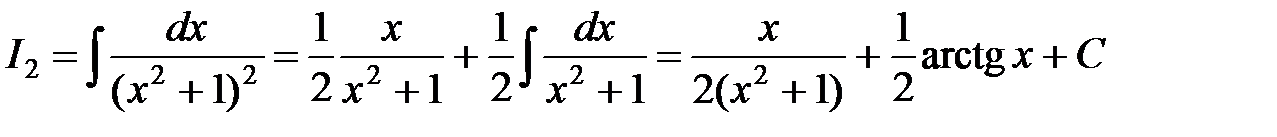 .
.
Тогда
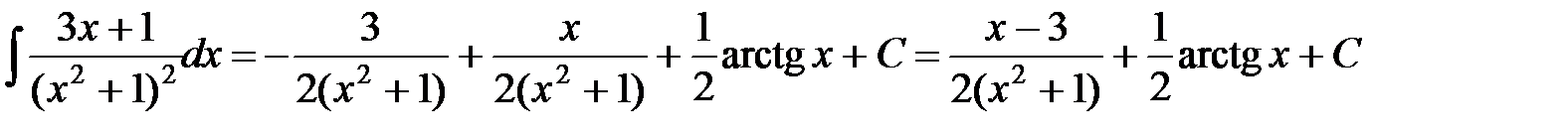 .◄
.◄
Дата добавления: 2016-04-14; просмотров: 948;
