Примеры решения задач. 1. Вычислить трехкратный интеграл .
1. Вычислить трехкратный интеграл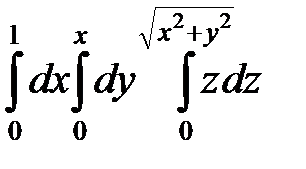 
.
► 
.◄
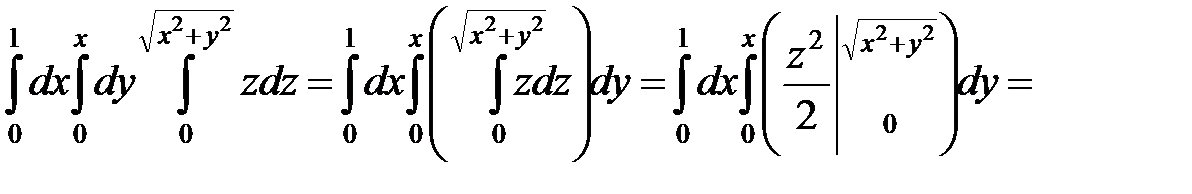
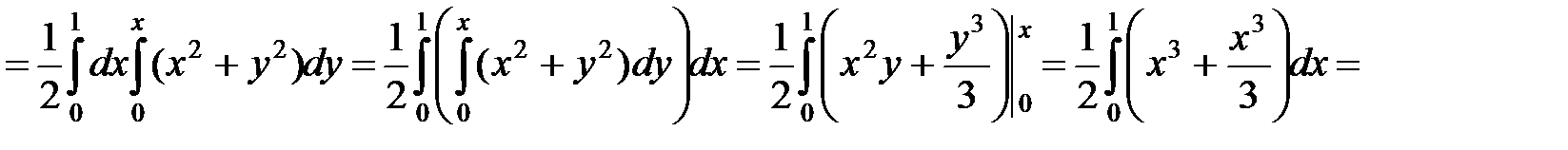
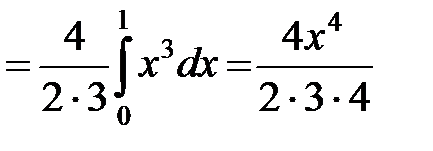
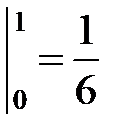2. Вычислить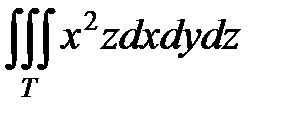 
, если область Т ограничена плоскостями
.
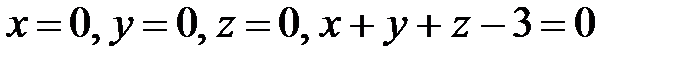| z |
| x |
| y |
| T |
| Рис. 8 |
| Рис. 9 |
| x |
| y |
| D |
► Область Т ограничена сверху плоскостью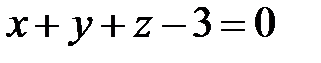 
, снизу − плоскостью 
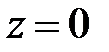, с боковых сторон − плоскостями 
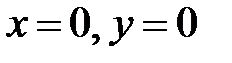. Изобразим эту область и ее проекцию D на плоскость 
:
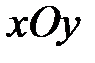При вычислении тройной интеграл приводится к двойному интегралу по проекции D области Т на плоскость 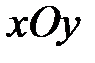и однократному интегралу по переменной z, а затем последовательно вычисляется трехкратный интеграл.
.◄
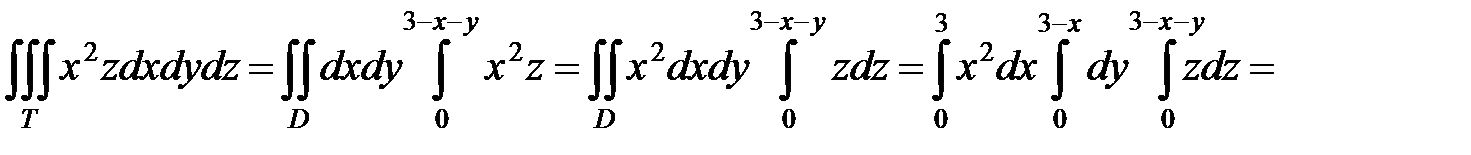
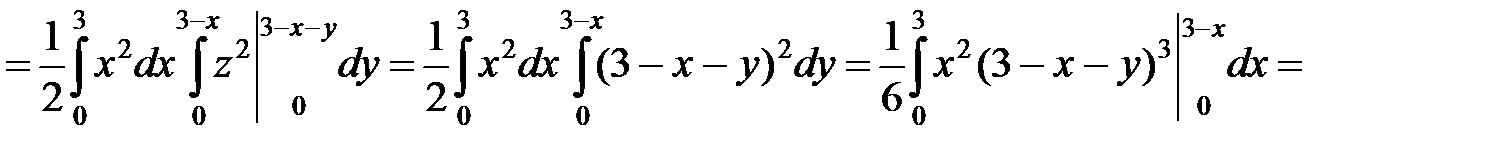
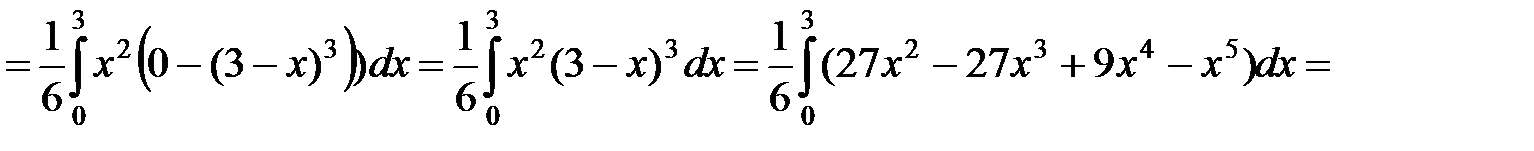
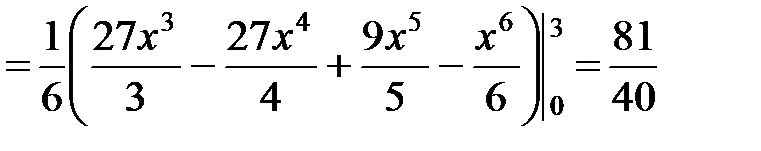3. Вычислить тройной интеграл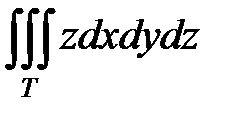 
, где Т − область, ограниченная сферой 
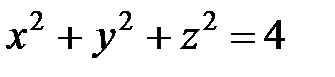и параболоидом вращения 
.
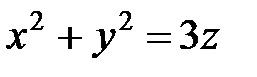| y |
| x |
|
|
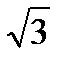
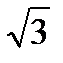
| D |
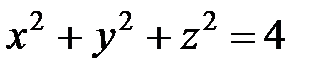определяет сферу с центром в начале координат и радиусом R=2, поверхность 
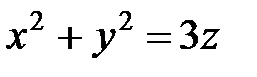− параболоид вращения вокруг оси 
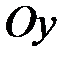. Построим проекциюD области Т на плоскость 
:
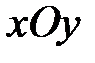| Рис. 10 |
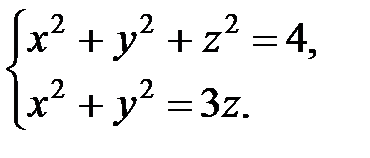
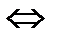
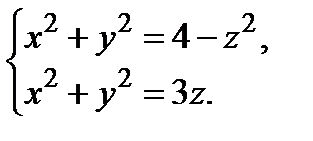
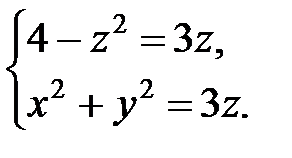
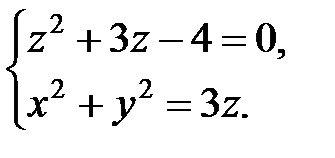
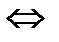
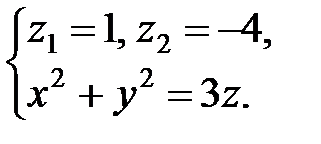
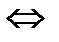
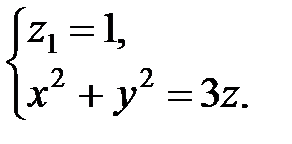
Отсюда получаем область D − круг радиуса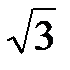 
, центр которого совпадает с началом координат, т.е. D: 
.
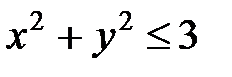Перейдем в тройном интеграле к цилиндрическим координатам. В цилиндрических координатах уравнение сферы: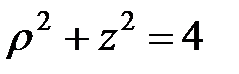 
или 
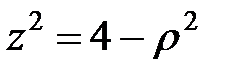; уравнение параболоида вращения: 
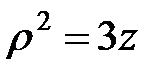или 
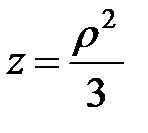; уравнение окружности 
.
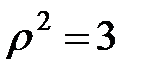Итак,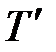 
: 
, 
.
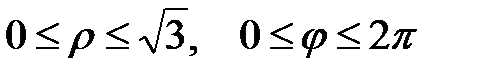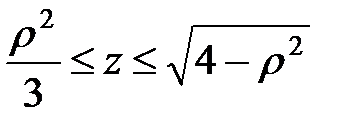По формуле тройного интеграла в цилиндрических координатах
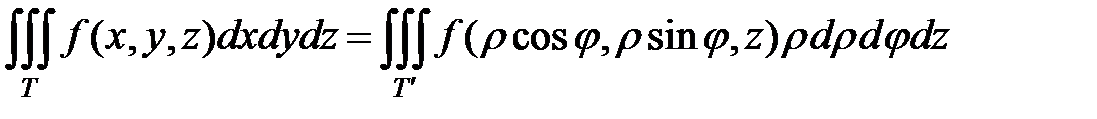(5.3)
имеем:
.◄
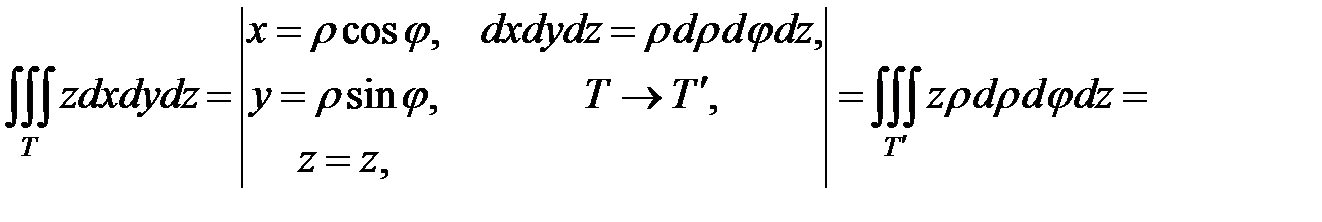
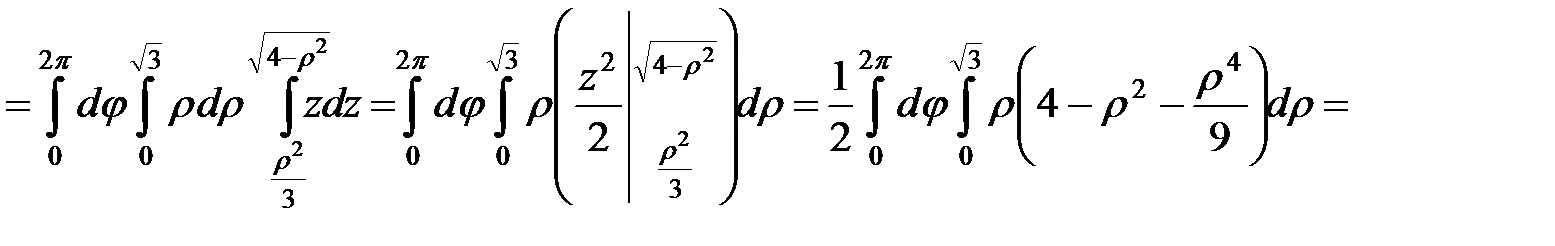
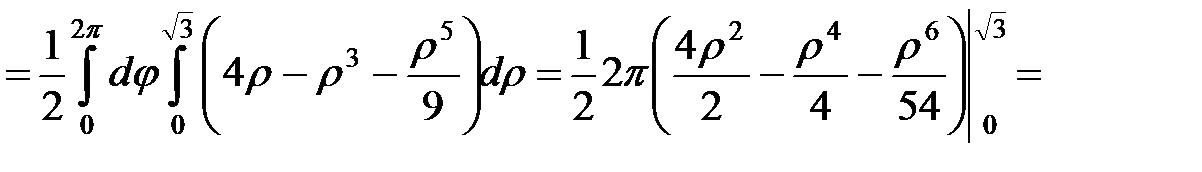
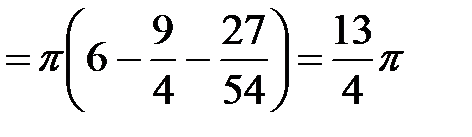Дата добавления: 2016-04-14; просмотров: 1312;