Примеры решения задач. 1. Исследовать на сходимость интеграл:
1. Исследовать на сходимость интеграл:
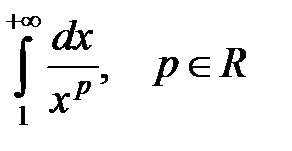 .
.
►Рассмотрим случаи 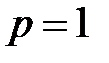 и
и 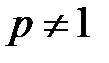 .
.
а) 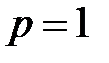 ;
; 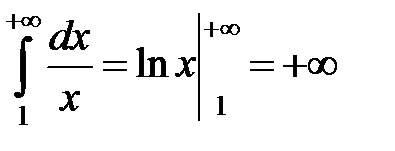 − интеграл расходится;
− интеграл расходится;
б) 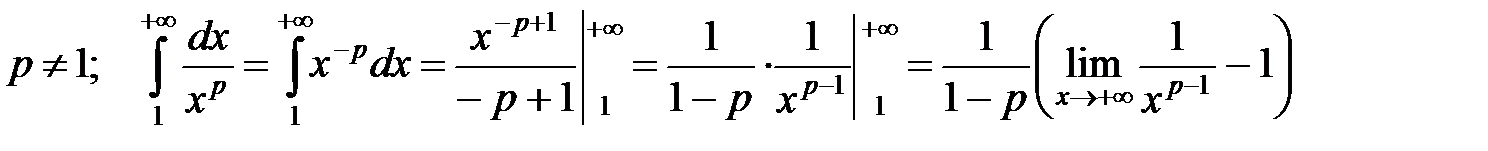 .
.
Далее рассмотрим случаи 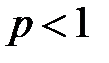 и
и 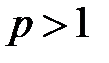 .
.
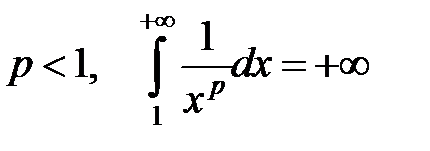 − интеграл расходится;
− интеграл расходится;
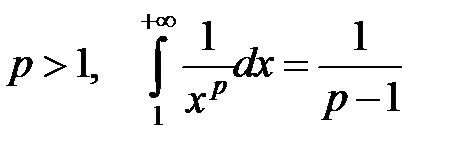 − интеграл сходится.
− интеграл сходится.
Итак, несобственный интеграл
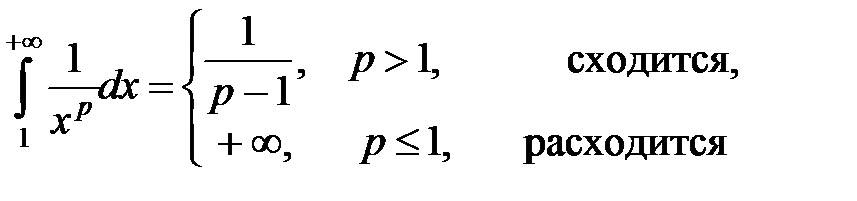 ◄
◄
2. Вычислить несобственные интегралы:
а) 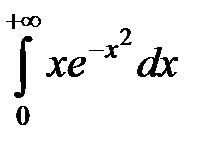 ; б)
; б) 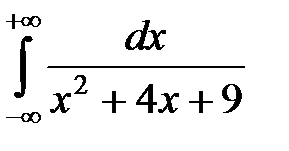 .
.
►а) Используем формулу Ньютона-Лейбница (см. приложение):
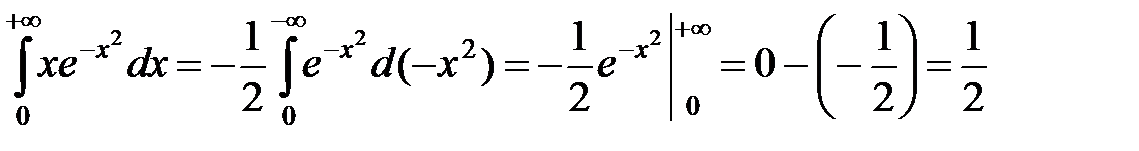 .
.
б) По формуле Ньютона-Лейбница имеем:
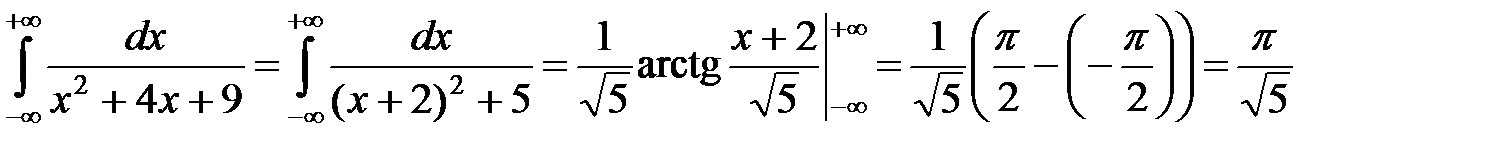 .◄
.◄
3. Исследовать на сходимость интегралы:
а) 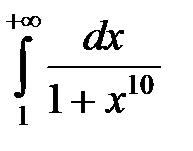 ; б)
; б) 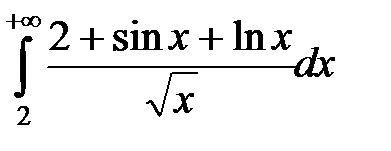 ; в)
; в) 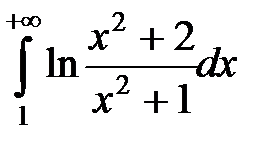 .
.
►а) Подынтегральная функция 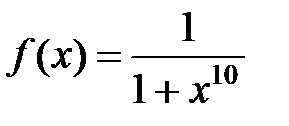 в промежутке интегрирования меньше, чем функция
в промежутке интегрирования меньше, чем функция 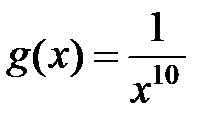 , т.е.
, т.е. 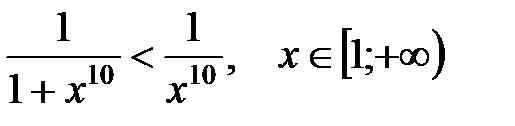 и интеграл
и интеграл
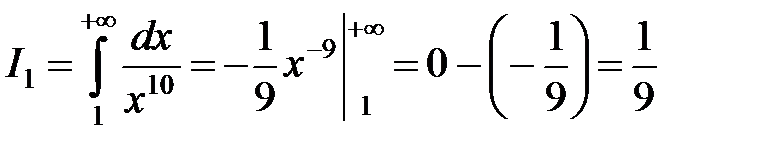 , т.е. сходящийся.
, т.е. сходящийся.
Тогда и интеграл 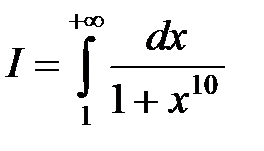 по признаку сравнения также сходящийся, причем
по признаку сравнения также сходящийся, причем 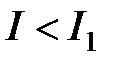 .
.
б) Для сравнения с подынтегральной функцией
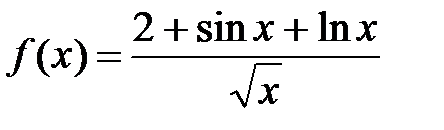
возьмем функцию 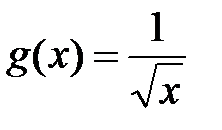 .
.
Имеем 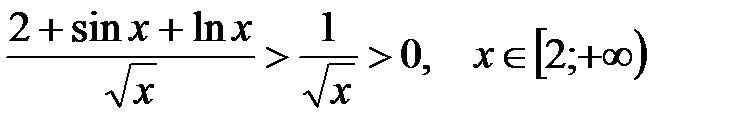 ,
,
а интеграл 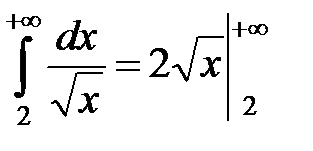 расходится, тогда и данный интеграл также расходится.
расходится, тогда и данный интеграл также расходится.
в) Подынтегральную функцию
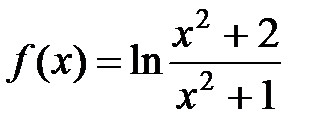
сравним с функцией 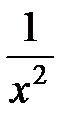 , т.е. рассмотрим
, т.е. рассмотрим
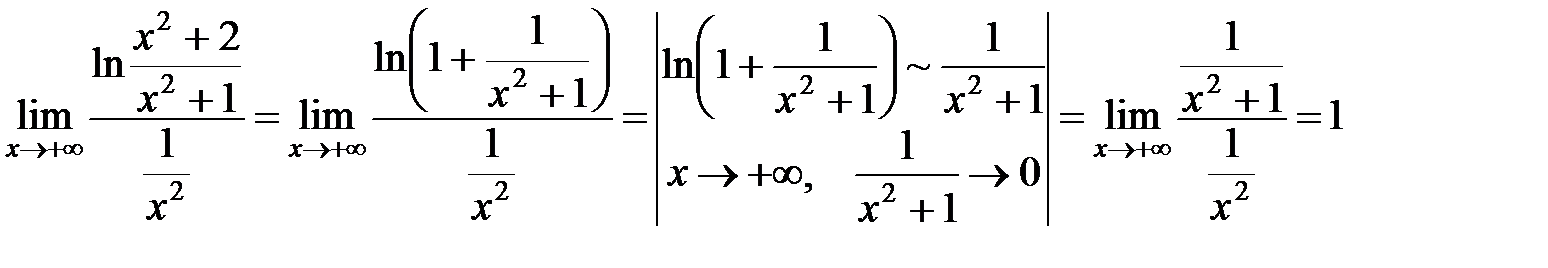 .
.
Согласно предельному признаку сравнения получаем, что, так как интеграл 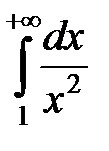 сходится, то данный интеграл также сходится.◄
сходится, то данный интеграл также сходится.◄
4. Исследовать на сходимость интеграл
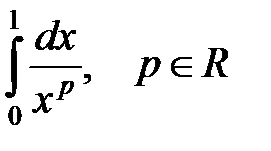 .
.
►Если 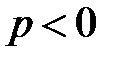 , то интеграл не является несобственным.
, то интеграл не является несобственным.
Если 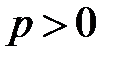 , то имеем несобственный интеграл второго рода; точка
, то имеем несобственный интеграл второго рода; точка 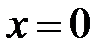 − особая точка подынтегральной функции на промежутке интегрирования.
− особая точка подынтегральной функции на промежутке интегрирования.
При 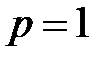 имеем
имеем
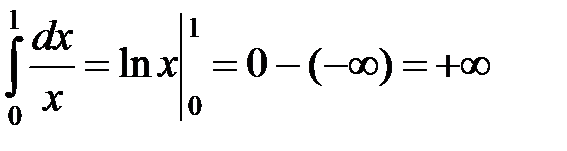 − интеграл расходится.
− интеграл расходится.
При 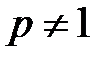 имеем
имеем
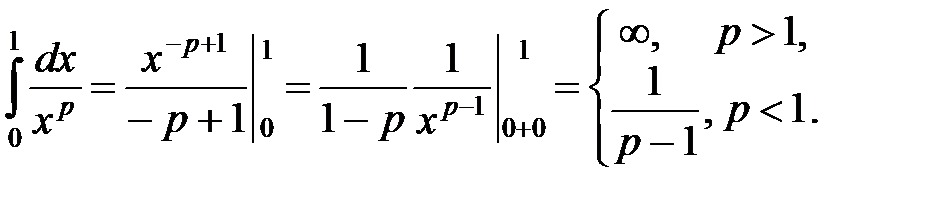
Итак,
 ◄
◄
5. Вычислить интегралы:
а) 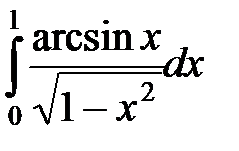 ; б)
; б) 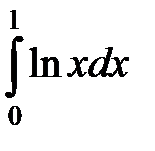 .
.
►а) Точка 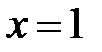 − особая точка подынтегральной функции на промежутке
− особая точка подынтегральной функции на промежутке 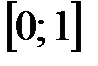 .
.
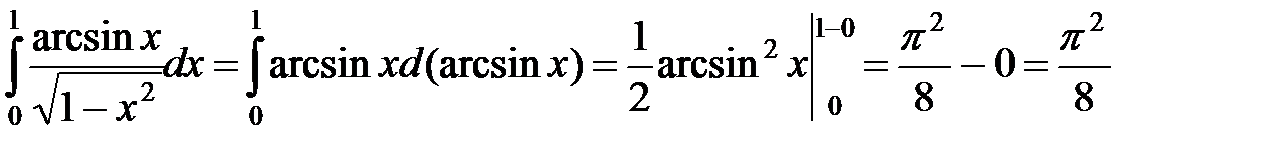 .
.
б) Точка 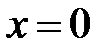 − особая точка подынтегральной функции на промежутке
− особая точка подынтегральной функции на промежутке 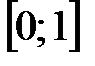 .
.
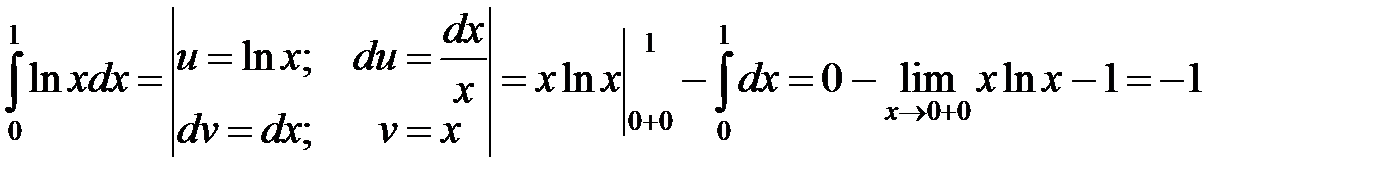 .
.
Здесь
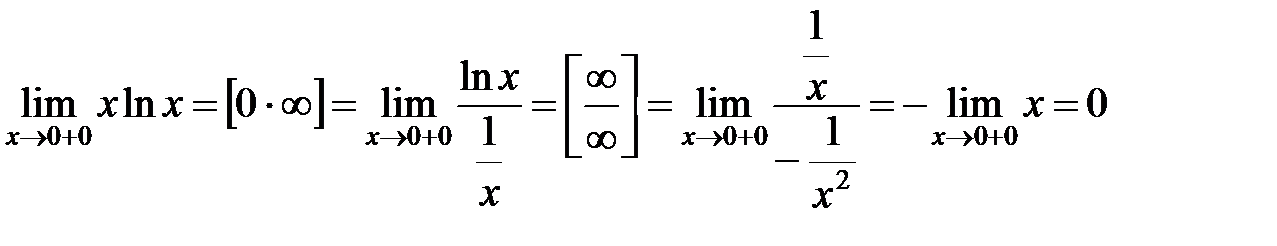 .◄
.◄
6. Исследовать на сходимость интегралы:
а) 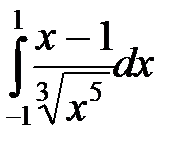 ; б)
; б) 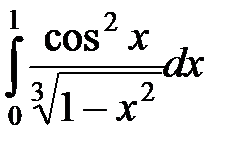 ; в)
; в) 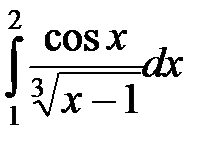 .
.
►а) На данном промежутке интегрирования точка 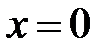 − особая, функция
− особая, функция 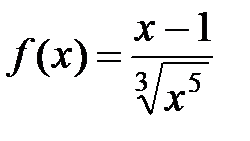 в этой точке неограниченна. Имеем несобственный интеграл второго рода:
в этой точке неограниченна. Имеем несобственный интеграл второго рода:
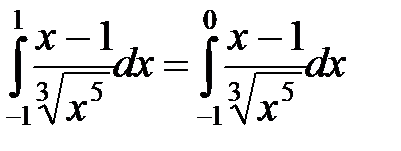 .
.
Рассмотрим первый интеграл:
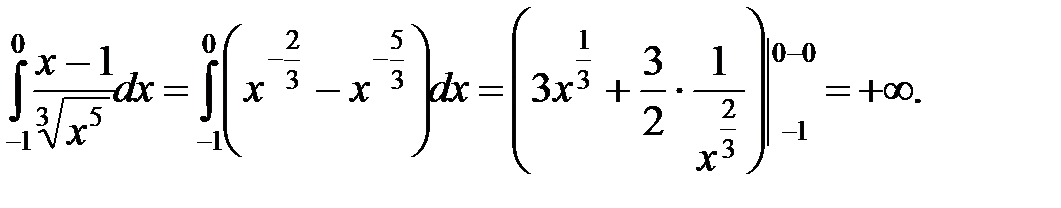
Этот интеграл расходящийся. Следовательно, и данный интеграл расходящийся.
б) Особая точка 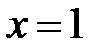 . Подставим подынтегральную функцию в виде:
. Подставим подынтегральную функцию в виде:
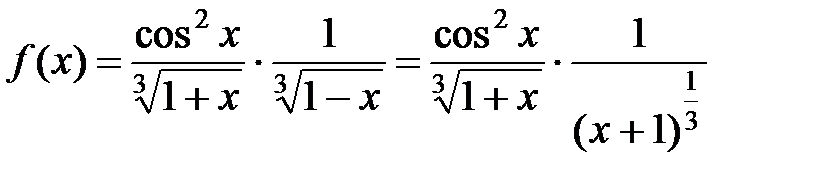 .
.
Сравним данный интеграл с интегралом вида
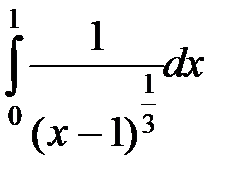 , который является сходящимся, т.к.
, который является сходящимся, т.к. 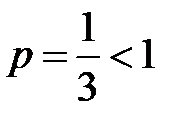 (см. пример 4).
(см. пример 4).
Сформулируем предельный признак сравнения.
Пусть 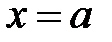 − особая точка функций
− особая точка функций 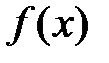 и
и 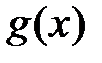 на
на 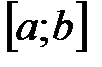 и
и 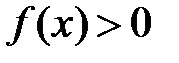 ,
, 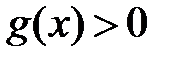 на
на 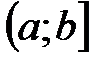 . Тогда, если существует конечный предел
. Тогда, если существует конечный предел
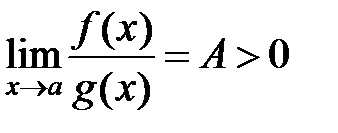 ,
,
то оба интеграла 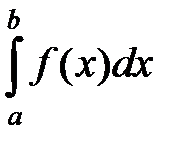 и
и 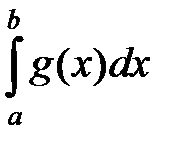 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Согласно данному признаку , исходный интеграл также сходящийся, т.к.:
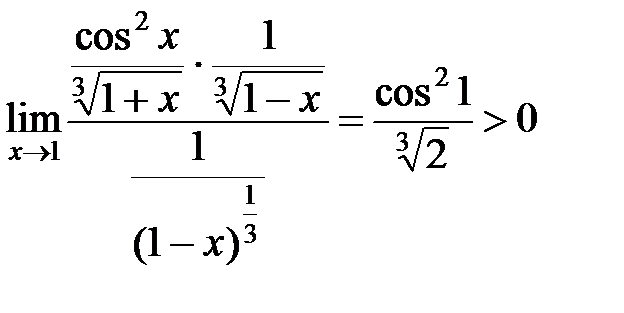 .
.
в) Особая точка 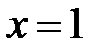 . Данный интеграл абсолютно сходящийся, т.к.:
. Данный интеграл абсолютно сходящийся, т.к.:
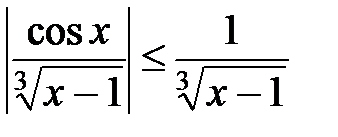 и интеграл
и интеграл 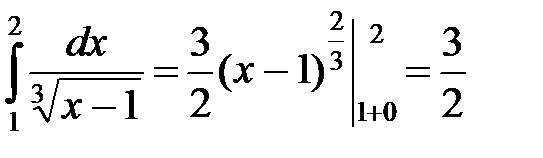 сходится.◄
сходится.◄
Дата добавления: 2016-04-14; просмотров: 3651;
