Примеры решения задач. 1. Вычислить криволинейный интеграл первого рода , где L − дуга плоской кривой при .

1. Вычислить криволинейный интеграл первого рода 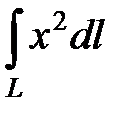, где L − дуга плоской кривой 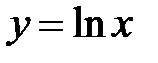при .

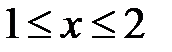► Найдем дифференциал длины дуги 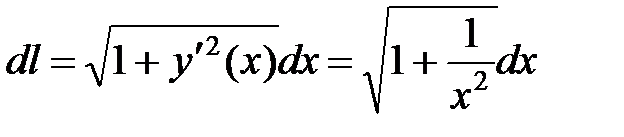и применим формулу

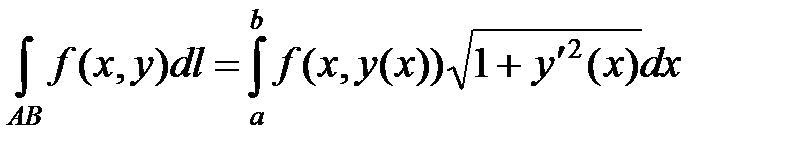(5.1)

.◄

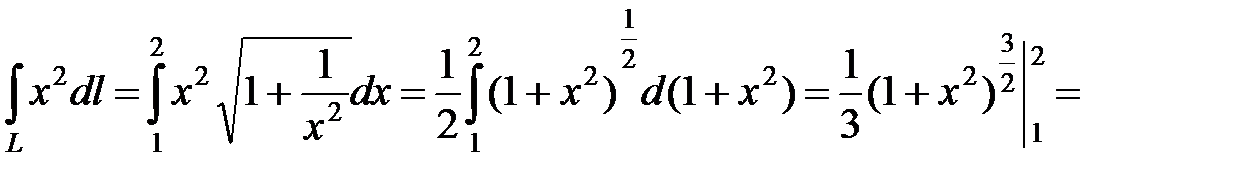
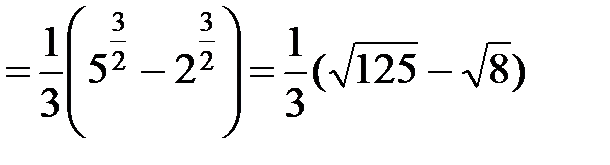2. Вычислить криволинейный интеграл первого рода 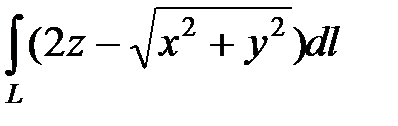, где L − первый виток конической винтовой линии

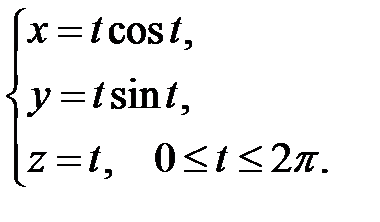
► Так как 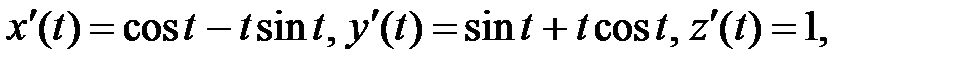то

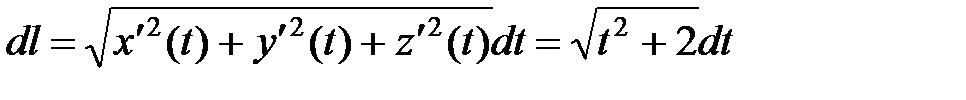и по формуле вычисления криволинейного интеграла для кривой, заданной в параметрическом виде,

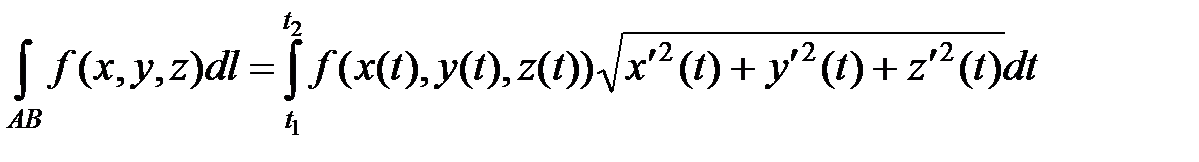(5.2)

имеем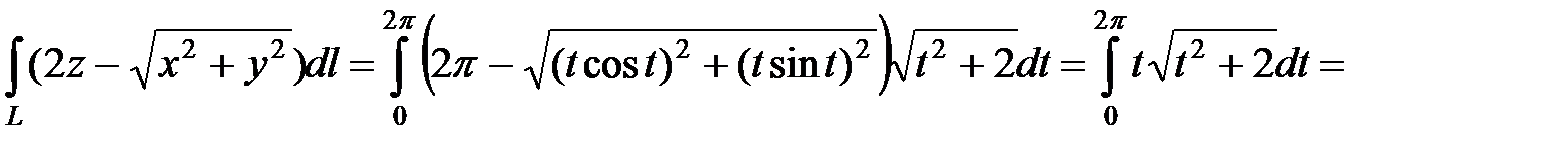

.◄

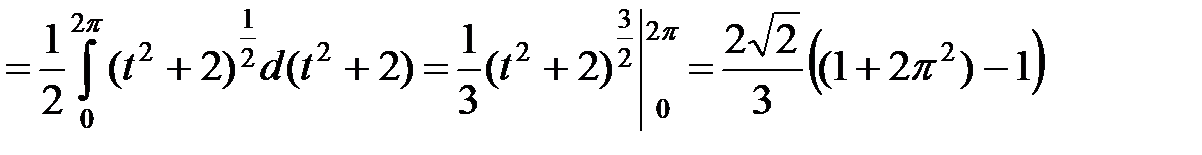3. Вычислить криволинейный интеграл первого рода 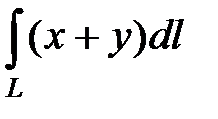, где L − лепесток лемнискаты Бернулли 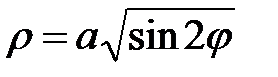, расположенной в I координатной четверти.

► Используем формулу

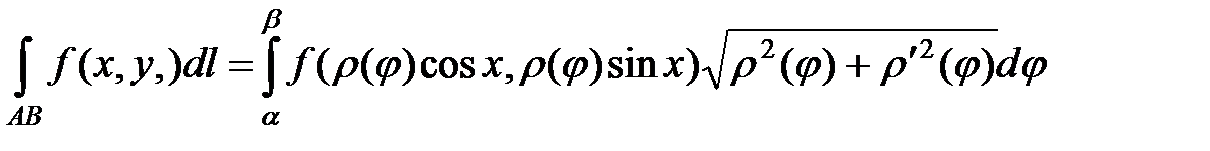, (5.3)

если кривая АВ задана в полярной системе координат.

; ;

.

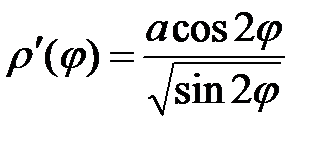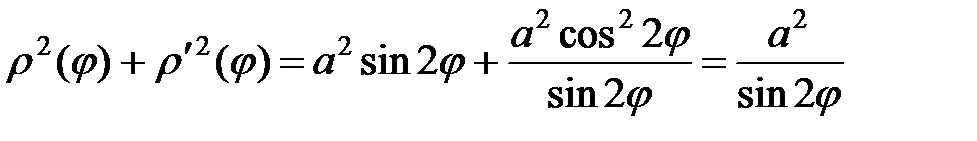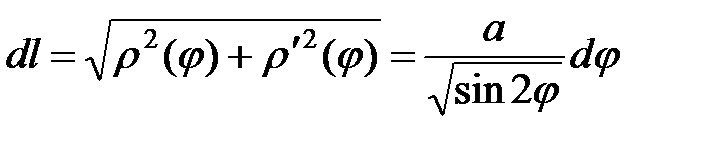В I координатной четверти полярная координата 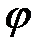меняется от 0 до 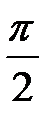, тогда

.◄

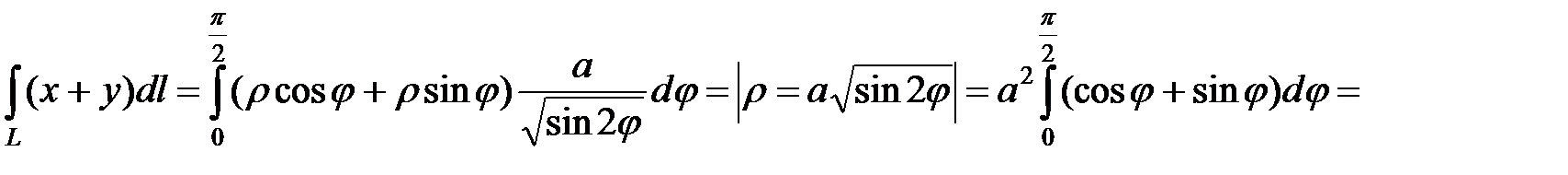
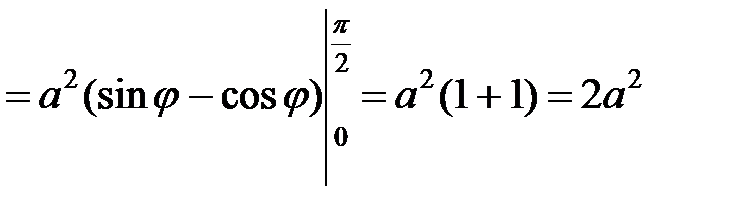Задания для самостоятельной работы

5.1. Вычислить криволинейные интегралы первого рода:

1) 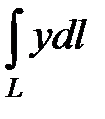, где L − дуга параболы от точки А (0; 0) до точки В (1;1);

2) 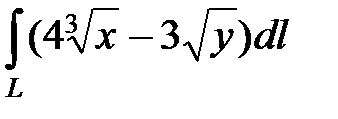, где L − отрезок прямой от точки А (-1; 0) до точки В (0; 1);

3) 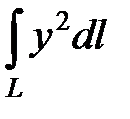, где L − четверть круга ;

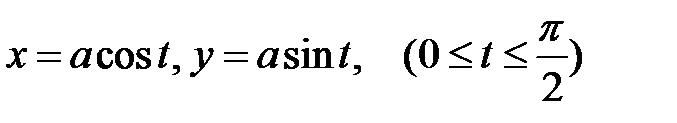4) 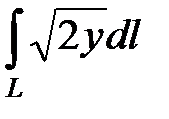, где L − первая арка циклоиды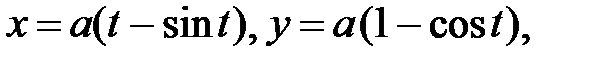

;

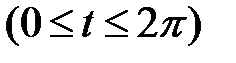5) 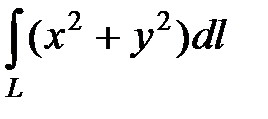, где L − дуга логарифмической спирали 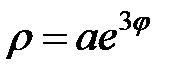от точки

А (а; 0) до точки О (0; 0).

Криволинейный интеграл второго рода по координатам