Примеры решения задач. 1. Вычислить площадь фигуры, ограниченной прямой и кривой .
1. Вычислить площадь фигуры, ограниченной прямой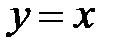 
и кривой 
.
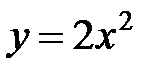| Рис.1 |
| у |
| х |
|
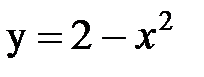
| -2 |
|
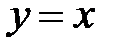
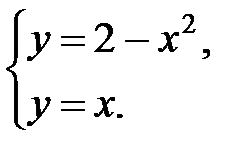
Получим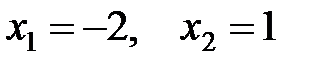 
. Это и есть пределы интегрирования. Тогда, по формуле
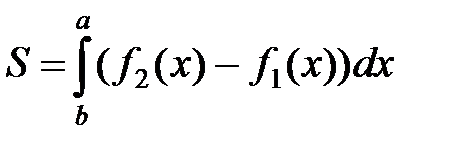. (2.1)
находим площадь:
.◄
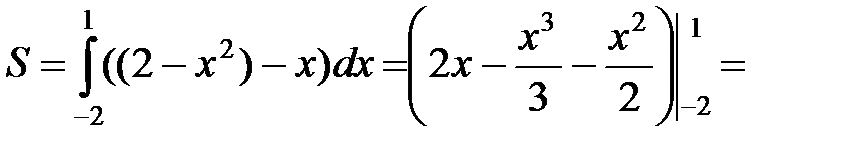
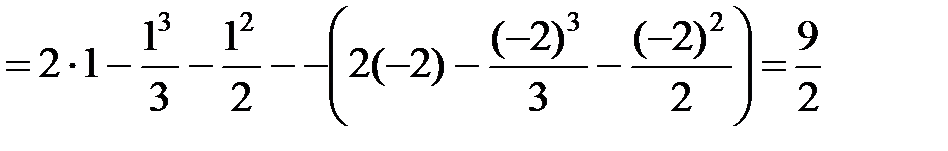| y |
| x |
|
.
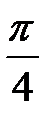
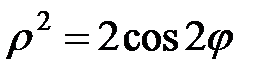►Кривая задана в полярной системе координат.
Имеет место формула:
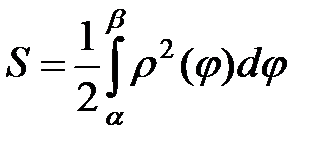. (2.2)
| Рис. 2 |
При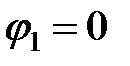 
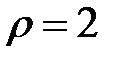, при 
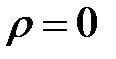
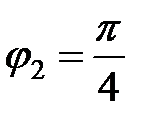, т.е. 
.
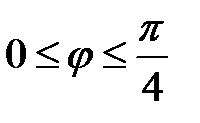Имеем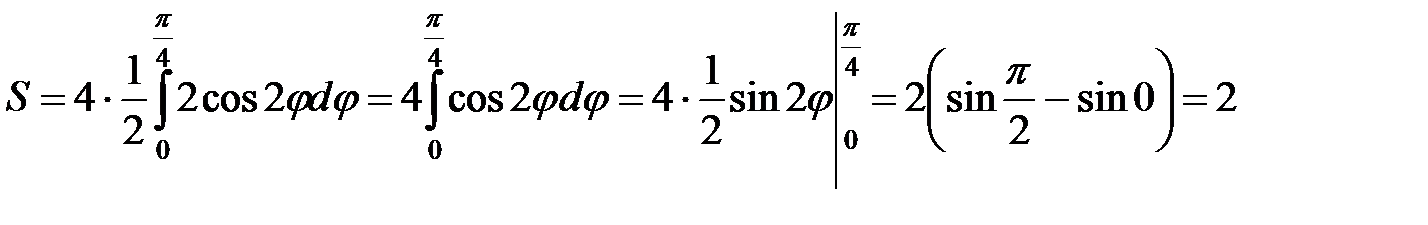 
.◄
3. Вычислить объем тела, полученного вращением вокруг оси Оx криволинейной трапеции, ограниченной линиями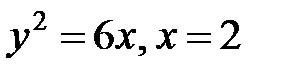 
и оси Оx.
►Для нахождения объема будем использовать формулу
.
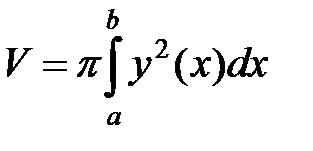В пределах данной трапеции х меняется от 0 до 2, значит,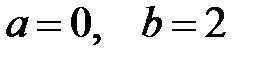 
. Тогда
.◄
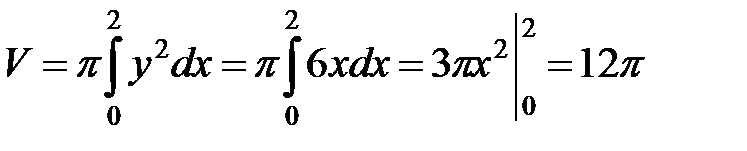4. Найти длину дуги кривой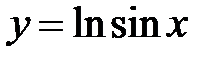 
, заключенной между точками с абсциссам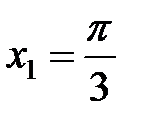и 
и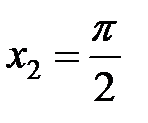 
.
►Для вычисления длины дуги 
применим формулу:
.
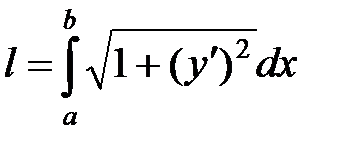В данном случае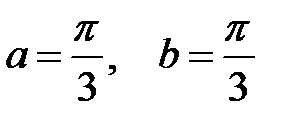 
, 
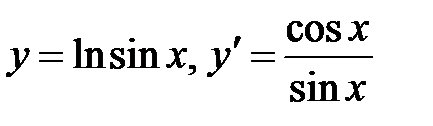. Тогда
◄
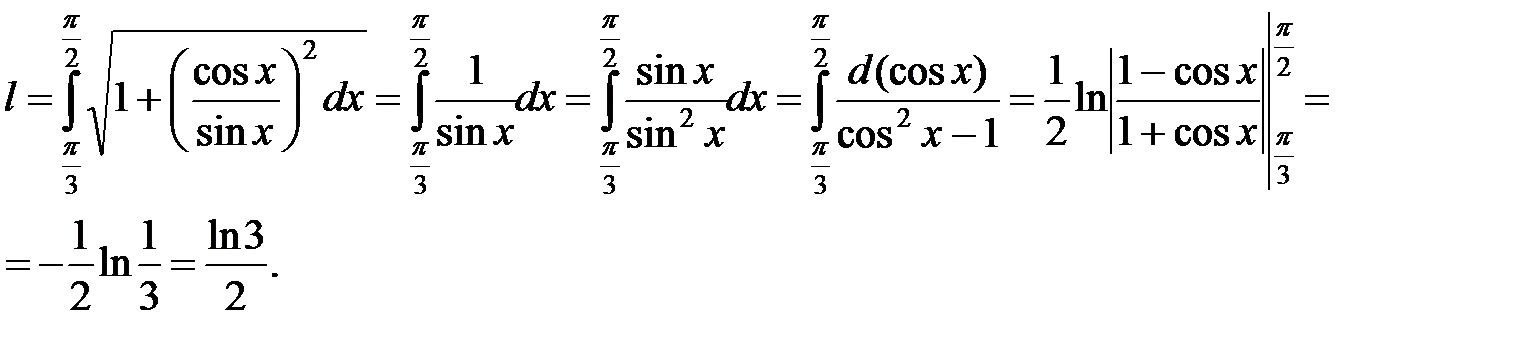5. Найти работу, затраченную на выкачивание жидкости из конического резервуара, обращенного вершиной вниз, если высота резервуара равна Н, радиус основания R.
►Вычислим вес элементарного слоя жидкости, находящейся на глубине х.
Высоту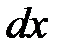 
этого слоя выберем таким образом, чтобы сделать этот слой цилиндром радиуса 
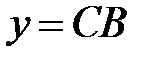. Тогда вес 
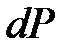этого слоя равен:
| y |
| х |
|
|
|
|
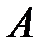
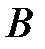
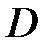
| y |
| х |
|
,
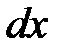
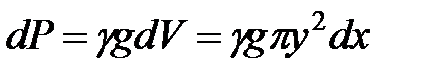где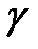 
− плотность жидкости, 
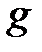− ускорение свободного падения, 
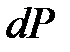− объем цилиндра.
Из подобия треугольников АОD и СВD находим у:
.
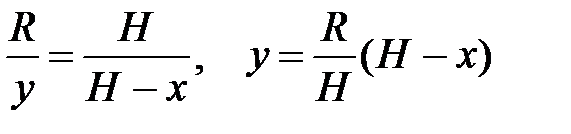| Рис. 3 |
.
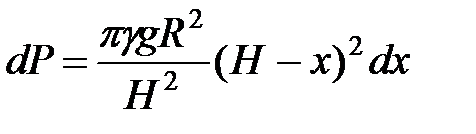Элементарная работа, затраченная на поднятие этого слоя жидкости на высоту х, равна
,
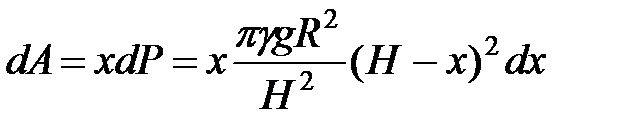поэтому
.◄
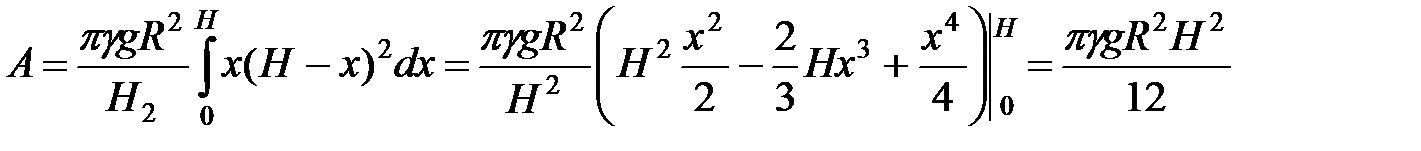6. Найти силу давления воды на вертикальную стенку в форме полукруга, радиус которого R=3м.
►По закону Паскаля сила давления жидкости на площади вычисляется по формуле:
,
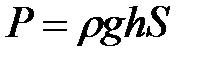где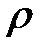 
− плотность жидкости, 
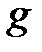− ускорение силы тяжести, 
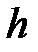− глубина погружения, 
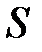− площадь площадки.
| y |
| х |
|
|
|
|
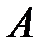
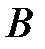
| y |
| х |
|
|
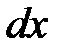
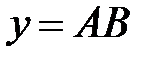и высоты 
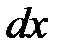. Из треугольника 
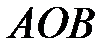имеем:
.
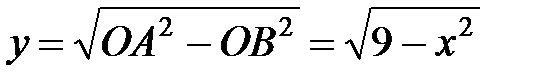| Рис. 4 |
.
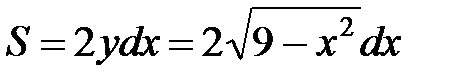Найдем дифференциал давления на элементарную площадку:
.
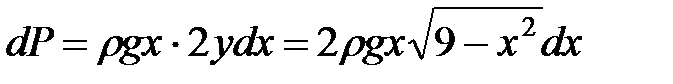Итак,
.◄
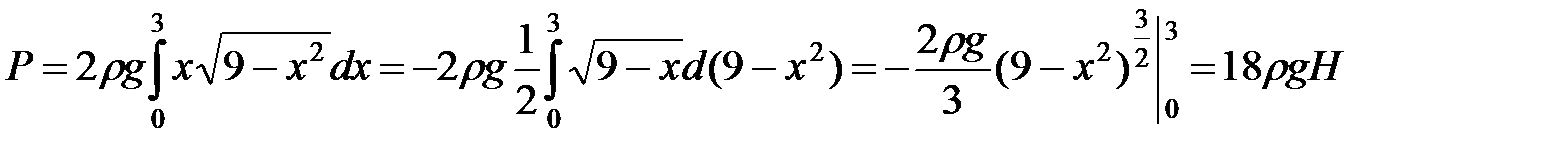Дата добавления: 2016-04-14; просмотров: 1325;