Закон радиоактивного распада. Радиоактивный распад – это случайное событие в «жизни» атома, можно сказать, несчастный случай

Радиоактивный распад – это случайное событие в «жизни» атома, можно сказать, несчастный случай. Попробуем исходя из этого весьма общего соображения вывести закон, по которому должна изменяться концентрация радиоактивных атомов со временем.

Пусть в некоторый момент времени t концентрация радиоактивного изотопа была равна п(t), а через малое время Dt стала равна п(t + Dt). Ясно, что за время Dt распалось п(t) – п(t + Dt) атомов.

Если радиоактивный распад – процесс случайный, то вполне логично предположить, что количество распадов за время Dt будет тем больше, чем больше концентрация атомов п(t) и чем больше промежуток времени Dt:

п(t) – п(t + Dt) ~ п(t) × Dt

или

п(t) – п(t + Dt) = lп(t)Dt, (1)

где l – коэффициент пропорциональности. Понятно, что у каждого изотопа этот коэффициент свой: если изотоп распадается быстро, то коэффициент l большой, если медленно, то маленький.

Перепишем равенство (1) в виде:

п(t + Dt) – п(t) = –lп(t)Dt. (2)

А теперь устремим Dt к нулю и заметим, что п(t + Dt) – п(t) – это приращение функции п(t) за время Dt, получим:

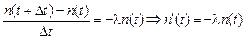. (3)

Мы получили дифференциальное уравнение. Ясно, что если в начальный момент концентрация изотопа была равна п₀, то п(0) = = п₀. «Угадаем» решение уравнения (3):

п(t) = п₀е^–lt. (4)

Проверим, подставив выражение (4) в уравнение (3):

л.ч.: (п₀е^–lt)¢ = п₀е^–lt(–l);

п.ч.: –lп₀е^–lt.

Очевидно, что левая часть тождественно равна правой, кроме того, выполняется и начальное условие:

п(0) = п₀е^–l×0 = п₀е⁰ = п₀×1 = п₀.

Итак, мы получили закон радиоволнового распада:

п(t) = п₀е^–lt. (25.1)

Величину l называют постоянной радиоактивного распада.

Период полураспада

При изучении радиоактивного распада вместо постоянной распада как характеристики скорости процесса часто пользуются другой величиной – периодом полураспада.

Период полураспада Т – это время, в течение которого распадается половина первоначального количества данного радиоактивного изотопа. Найдем связь между Т и l.

Воспользуемся тем математическим фактом, что для любого числа а справедливо равенство .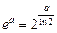

В самом деле,

lne^a = alne = a×1 = a и .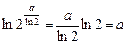

Тогда перепишем формулу (25.1) в виде

.

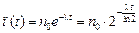Введем обозначение

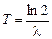. (25.2)

Тогда

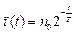. (25.3)

Если в формулу (25.3) подставить значение t = T, получим

.

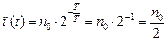Таким образом, 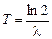– этот период полураспада данного изотопа.

Надо сказать, что у разных изотопов периоды полураспада могут принимать самые разные значения. Например:

₉₂U²³⁸ (a-распад): Т = 4,5×10⁹ лет;

₉₄Pu²³⁹ (a-распад): Т = 24400 лет;

₈₉Ra²³⁶ (a-распад): Т = 1600 лет;

₉₁Ас²³³ (b^–-распад): Т = 27 сут.;

₉₀Th²³³ (b^–-распад): Т = 22 мин.

Существуют изотопы, у которых период полураспада составляет десятитысячные доли секунды (некоторые изотопы полония ₈₄Ро).

Задача 25.2. Радиоактивный изотоп углерода 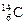в старом куске дерева составляет 0,0416 массы этого изотопа в живых растениях. Каков возраст этого куска дерева? Период полураспада изотопа 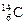равен 5570 годам.

т(t) = 0,0416т0 Т = 5570 лет	Решение. Поскольку масса изотопа прямо пропорциональна концентрации его атомов: ,
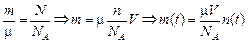t = ?

то масса изменяется по такому же закону, что и концентрация

m(t) = m₀ 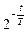. (1)

Выразим из уравнения (1) неизвестную t:

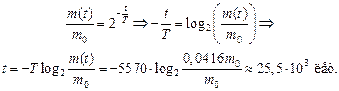
Ответ: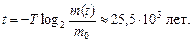

СТОП! Решите самостоятельно: А6, В3, С2.

Задача 25.3. Определить период полураспада радона, если за 1 сут из 1 млн. атомов распадается 175000 атомов.

убыли числа атомов радона к исходному числу атомов:

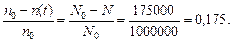
Воспользуемся формулой (25.3), получим

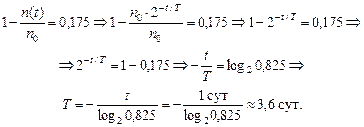
Ответ: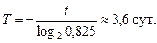

СТОП! Решите самостоятельно: В2, В4, С3, D1.