Массы некоторых изотопов
| Изотоп | Масса нейтрального атома, а.е.м. | Изотоп | Масса нейтрального атома, а.е.м. |
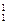 Н (водород) Н (водород)
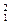 H (дейтерий) H (дейтерий)
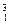 H (тритий) H (тритий)
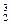 Нe (гелий) Нe (гелий)
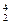 Не (гелий) Не (гелий)
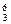 Li(литий) Li(литий)
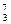 Li(литий) Li(литий)
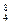 Ве (бериллий) Ве (бериллий)
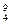 Ве (бериллий) Ве (бериллий)
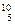 B (бор) B (бор)
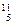 В (бор) В (бор)
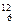 C (углерод) C (углерод)
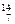 N (азот) N (азот)
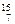 N (азот) N (азот)
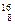 О(кислород) О(кислород)
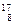 О (кислород) О (кислород)
| 1,00783 2,01410 3,01605 3,01602 4,00260 6,01513 7,01601 8,00531 9,01219 10,01294 11,00931 12,00000 14,00307 15,00011 15,99491 16,99913 | 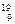 F (фтор) F (фтор)
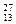 Al (алюминий) Al (алюминий)
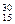 P (фосфор) P (фосфор)
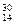 Si (кремний) Si (кремний)
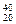 Ca (кальций) Ca (кальций)
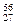 Co (кобальт) Co (кобальт)
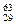 Cu (медь) Cu (медь)
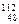 Cd (кадмий) Cd (кадмий)
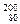 Hg (ртуть) Hg (ртуть)
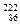 Rn (родон) Rn (родон)
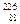 Ra (радий) Ra (радий)
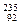 U (уран) U (уран)
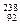 U (уран) U (уран)
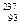 Np (нептуний) Np (нептуний)
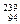 Pu (плутоний) Pu (плутоний)
| 18,99843 26,98153 29,97867 29,97377 39,96257 55,93984 62,92960 111,90276 199,96832 222,01922 226,02435 235,04299 238,05006 237,04706 239,05122 |
Находим в табл. 26.1 и 26.2 значения:
масса атома 1Н2: 2,01410 а.е.м.,
масса протона: 1,00728 а.е.м.,
масса нейтрона: 1,00866 а.е.м.,
масса электрона: 0,00055 а.е.м.
Масса ядра 1Н2 = (масса атома1Н2) – (масса электрона) =
=2,01410 – 0,00055 = 2,01355 а.е.м.;
(масса протона + масса нейтрона) = 1,00728 + 1,00866 =
= 2,01594 а.е.м.
Как видим, 2,01594 > 2,01355!
Разницу между массами нуклонов, составляющих ядро, и массой самого ядра называют дефектом массы.
Для дейтерия, как нетрудно подсчитать, дефект массы составляет 2,01594 – 2,01355 = 2,39×10–3 а.е.м. А зная дефект массы, нетрудно подсчитать и энергию связи в ядре: Есв = Dтс2.
Задача 26.4. Вычислить дефект массы, энергию связи и удельную энергию связи ядра гелия 2Не4 (в МэВ).
| 2Не4 | Решение. Пусть тр – масса протона, тп – масса нейтрона, те – масса электрона, та – масса атома, тя – масса ядра, А – массовое число, Z – заряд ядра. В ядре содержится Z протонов и (A – Z) нейтронов, их суммарная масса равна Zmp + (A – Z)mn. |
| Dт = ? Есв = ? Еуд = ? | |
Масса атома складывается из массы ядра и массы Z электронов:
та = тя + Zme Þ тя = та – Zmе.
Тогда дефект массы ядра равен:
Dт = Zmp + (A – Z)mn – (та – Zmе) =
= Z(mp + те) + (A – Z)mn – та.
Учтем, что атом водорода 1Н1 – это как раз «протон+электрон», поэтому можно считать, что mp + те = тН, где тН – масса атома водорода 1Н1. Тогда формула для дефекта масса примет вид:
Dт = Zmн + (A – Z)mn – та. (26.3)
Применим формулу (26.3) к нашему случаю: Z = 2, А = 4, получим
Dт = 2mн + (4 – 2)mn – та.
Значение массы атомов водорода 1Н1 и 2Не4 находим в табл. 26.2, а значения массы нейтрона в табл. 26.1. Подставим в формулу численные значения и получим
Dт = 2×1,00783 + (4 – 2)×1,00866 – 4,00260 » 0,03038 а.е.м.
Вспомним, что 1 а.е.м. = 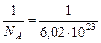 (г) =
(г) = 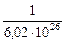 кг.
кг.
Переведем Dт в килограммы: Dт = 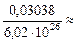 5,05×10–29 кг.
5,05×10–29 кг.
Теперь найдем энергию связи по формуле:
Есв = Dтс2, (26.4)
Есв = 5,05×10–29 кг × (3,0×108 м/с)2 » 4,55×10–12 Дж.
Переведем джоули в электрон-вольты:
Есв = 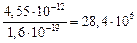 эВ » 28,4 МэВ.
эВ » 28,4 МэВ.
По формуле (26.2) найдем удельную энергию связи:
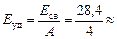 7,1 МэВ.
7,1 МэВ.
Ответ: Dт » 0,03038 а.е.м.; Есв » 28,4 МэВ; Еуд » 7,1 МэВ.
СТОП! Решите самостоятельно: А5–А7, В6–В8.
Задача 26.5. Выделяется или поглощается энергия в ядерной реакции 7N14 + 2Не4 ® 8О17 + 1Н1?
Решение. Чтобы ответить на вопрос задачи, необходимо выяснить, увеличивается или уменьшается масса системы в результате реакции. Масса атомов до реакции равна
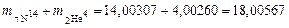 а.е.м.
а.е.м.
Масса атомов после реакции:
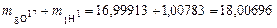 а.е.м.,
а.е.м.,
18,00696 > 18,00567.
Значит, энергия увеличилась: Е2 > Е1, поэтому чтобы реакция прошла, надо добавить «внешнюю» энергию. А в ходе реакции эта добавленная энергия будет поглощена: она пойдет на увеличение массы системы.
Ответ: энергия поглощается.
СТОП! Решите самостоятельно: В9.
Задача 26.6. Сколько энергии поглотится в ядерной реакции 7N14 + 2Не4 ® 8О17 + 1Н1?
Решение. Поглощенная энергия – это та энергия, которая пошла на увеличение массы системы: Е = Dтс2.
Величину Dт можно найти, воспользовавшись результатом предыдущей задачи:
Dт = 18,00696 – 18,00567 » 1,29×10–3 а.е.м.
Переведем а.е.м. в килограммы:
Dт = 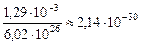 кг.
кг.
Тогда
Е = Dтс2 = 2,14×10–30×(3,0×108 м/с)2 » 1,93×10–13 Дж.
Переведем эту энергию в электрон-вольты:
Е = 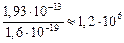 эВ = 1,2 МэВ.
эВ = 1,2 МэВ.
Ответ: Е = Dтс2 » 1,2 МэВ.
СТОП! Решите самостоятельно: В10, С1, С2.
Задача 26.7. Найти минимальную кинетическую энергию Wк протона, способного «разбить» ядро дейтерия на протон и нейтрон.
Решение.
Читатель: Это просто: Wк = Dтс2, где Dт – дефект массы ядра дейтерия.
Автор: Не совсем так. Ведь «осколки» деления – протон и нейтрон – будут иметь какие-то скорости, а значит, они будут обладать кинетической энергией. Кроме того, и «налетающий» протон после соударения будет иметь какую-то скорость.
Пусть начальная скорость протона υ0. Разобьем процесс его взаимодействия с ядром на два этапа: сначала ядро захватывает протон и составляет с ним одно целое, а затем распадается на три осколка: 2 протона и 1 нейтрон.
На первом этапе происходит неупругий удар. Считая массы протона и нейтрона примерно равными, можем записать закон сохранения импульса:
тυ0 = 3тu Þ 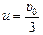 ,
,
где и – скорость ядра дейтерия с захваченным протоном.
Ясно, что если мы хотим вычислить минимальную энергию протона, то после распада составного ядра «осколки» должны иметь минимальные скорости относительно друг от друга, т.е. все они должны двигаться со скоростью υ0/3 на небольшом расстоянии друг от друга. Тогда их общая кинетическая энергия будет равна
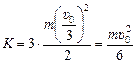 .
.
Итак, кинетическая энергия «налетающего» протона идет: 1) на увеличение массы системы; 2) на сообщение «осколкам», в число которых входит и сам протон, суммарной кинетической энергии 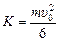 . Закон сохранения энергии запишется в виде:
. Закон сохранения энергии запишется в виде:
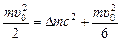 . (1)
. (1)
Учитывая, что 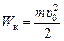 , получим
, получим 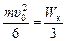 , тогда равенство (1) можно переписать в виде
, тогда равенство (1) можно переписать в виде
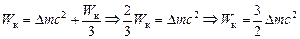 .
.
Дефект массы для ядра дейтерия мы уже подсчитывали раньше:
Dт = 2,39×10–3 а.е.м. = 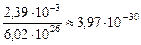 кг,
кг,
тогда
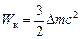 =
= 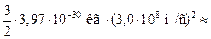
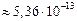 Дж.
Дж.
При желании можем перевести джоули в электрон-вольты:
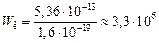 эВ = 3,3 МэВ.
эВ = 3,3 МэВ.
Ответ: 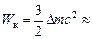 3,3 МэВ.
3,3 МэВ.
СТОП! Решите самостоятельно: В11, С3–С5.
Дата добавления: 2016-04-11; просмотров: 4475;
