Что может произойти, если в ядро попадет нейтрон?
1. Реакция захвата. Ее принято обозначать (п; g). Ядро захватывает нейтрон, при этом приходит в возбужденное состояние и испускает один или несколько g-квантов. Например, так:
(п; g): 92U235 + 0п1 ® 92U236 + g0.
Захватывать нейтроны «умеют» ядра всех изотопов.
2. Гораздо реже после захвата нейтрона ядро испускает протон или a-частицу. На это «способны» ядра очень немногих изотопов. Вот примеры таких реакций, которые называются реакциями (п; a) и (п; р) соответственно:
(п; a): 5В10 + 0п1 ® 2Не4 + 3Li7 (2Не4 – это a-частица);
(п; р): 7N14 + 0п1 ® 6С14 + 1Н1 (1Н1 – это протон).
3. Иногда после захвата нейтрона ядро испускает два нейтрона. Эта реакция называется реакцией (п; 2п). Эта реакция происходит только на тяжелых изотопах (z > 90) и при очень больших энергиях налетающих нейтронов (Е > 1 МэВ). Вот пример такой реакции:
(п; 2п): 94Pu240 + 0п1 ® 94Pu239 + 0п1 + 0п1.
4. Но самой важной для современного человечества является реакция деления (п; f)[4]. В этом случае после захвата нейтрона ядро распадается на два осколка примерно равной массы и, кроме того, испускаются еще 2–3 нейтрона. Но сразу заметим, что делятся под действием нейтронов только ядра тяжелых изотопов, у которых заряд ядра z ³ 90: Th, U, Pu и т.д.
Вот пример такой реакции:
(п; f): 92u235 + 0п1 ® 52Те138 + 40Zr96 + 30п1.
Забегая вперед, отметим, что в реакции деления тяжелых изотопов выделяется очень большая энергия, примерно 200 МэВ на один акт деления.
Как мы уже говорили, протоны и a-частицы, если их хорошенько разогнать и направить точно в ядро, тоже способны вступать с ядром в различные реакции: «выбивать» из ядра нейтроны, протоны, a-частицы и g-кванты.
Приведем два примера таких реакций:
(a; п): 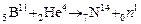 ;
;
(a; р): 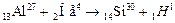 .
.
Задача 26.1. В результате захвата нейтрона ядром изотопа 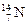 образуется неизвестный элемент и a-частица. Написать реакцию и определить неизвестный элемент.
образуется неизвестный элемент и a-частица. Написать реакцию и определить неизвестный элемент.
0п1; 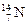 ; ; 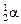
| Решение. Запишем ядерную реакцию
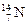 + 0п1 ® + 0п1 ® 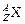 + + 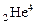 ,
где Х – неизвестный элемент, Z – заряд; А – массовое число. ,
где Х – неизвестный элемент, Z – заряд; А – массовое число.
|
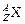 = ? = ?
| |
Электрический заряд в ходе реакции сохраняется, поэтому
7 + 0 = Z + 2 Þ Z = 7 – 2 = 5.
В таблице Менделеева пятый номер имеет бор (В). Сумма массовых чисел до реакции равна сумме массовых чисел после реакции, поэтому
14 + 1 = А + 4 Þ А = 11.
Следовательно, в результате реакции получаем изотоп 5В11. Итак, искомая реакция: 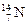 + 0п1 ®
+ 0п1 ® 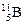 +
+ 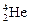 .
.
СТОП! Решите самостоятельно: А1–А3, В1.
Задача 26.2. Ядро изотопа урана 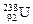 , захватив один нейтрон, разделилось на два осколка. При этом освободились два нейтрона. Один из осколков оказался ядром изотопа ксенона
, захватив один нейтрон, разделилось на два осколка. При этом освободились два нейтрона. Один из осколков оказался ядром изотопа ксенона 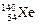 . Каким был второй осколок? Написать уравнение реакции.
. Каким был второй осколок? Написать уравнение реакции.
Решение. Запишем реакцию:
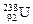 + 0п1 ®
+ 0п1 ® 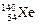 + 20п1 +
+ 20п1 + 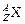 .
.
Действуя так же, как и в предыдущей задаче, найдем Z и А:
92 + 0 = 54 + 2×0 + Z Þ Z = 38.
Под 38-м номером в таблице Менделеева стоит элемент стронций (Sr). Найдем массовое число
235 + 1 = 140 + 2×1 + А Þ А = 94.
Значит, искомый изотоп – 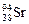 . Искомая реакция имеет вид
. Искомая реакция имеет вид
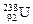 + 0п1 ®
+ 0п1 ® 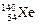 +
+ 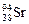 + 20п1.
+ 20п1.
СТОП! Решите самостоятельно: В2, В3.
Масса и энергия
Одним из важнейших выводов специальной теории относительности А. Эйнштейна было утверждение о том, что масса тела и его энергия связаны соотношением
Е = тс2. (26.1)
Эту энергию еще называют энергией покоя, т.е. сам факт наличия у тела массы означает наличие у него энергии. Более того, уменьшая массу тела, можно получить энергию в виде энергии излучения или в виде кинетической энергии.
Мы уже с вами говорили о позитроне – частице с массой электрона и положительным элементарным зарядом. Экспериментально установлено, что «при встрече» электрона с позитроном эти частицы аннигилируют (взаимно уничтожают друг друга), а вместо них появляется g-квант с энергией, равной сумме кинетических энергий частиц и их суммарной энергии покоя 2тес2 (где те – масса электрона). Наблюдается и обратный процесс: при определенных условиях g-квант может превратиться в пару частиц «электрон+позитрон». И тогда энергия g-кванта Е = hn пойдет на создание энергии покоя двух масс 2 тес2 и каких-то кинетических энергий образовавшихся частиц.
Задача 26.3. Фотон с энергией 3,0 МэВ превратился в пару электрон–позитрон. Найти кинетическую энергию каждой частицы в предположении, что она у обеих частиц одинакова.
| Е = 3,0 МэВ | Решение. Энергия фотона пошла на то, чтобы: 1) обеспечить двум появившимся частицам их энергии покоя тес2 каждой; 2) сообщить им одинаковые |
| K = ? | |
кинетические энергии 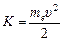 . Закон сохранения энергии можно записать в виде
. Закон сохранения энергии можно записать в виде
Е = 2тес2 + 2K Þ 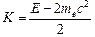 . (1)
. (1)
Масса электрона – табличная величина: те = 9,1×10–31 кг. Вспомним, что 1 эВ = 1,6×10–19 Дж, переведем энергию фотона из МэВ в джоули: 3 МэВ = 3×106 × (1,6×10–19) Дж » 4,8×10–13 Дж и подставим в формулу (1) численные значения:
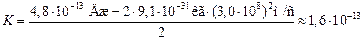 Дж.
Дж.
При желании можно перевести джоули в электрон-вольты:
1 эВ = 1,6×10–19 Дж Þ 1 Дж = 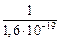 эВ.
эВ.
Получим 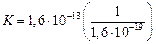 эВ » 1,0×106 эВ = 1,0 МэВ.
эВ » 1,0×106 эВ = 1,0 МэВ.
Ответ: 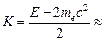
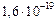 Дж = 1,0 МэВ.
Дж = 1,0 МэВ.
СТОП! Решите самостоятельно: А4, В4, В5.
Энергия связи
Нуклоны в ядре связаны между собой мощными силами ядерного взаимодействия. Поэтому чтобы вырвать нуклон из ядра, внешним силам надо совершить работу. А ядерные силы, сопротивляясь, будут совершать отрицательную работу.
Вспомним, что аналогичная ситуация происходит при удалении электрона от ядра: тогда силы кулоновского притяжения тоже совершают отрицательную работу. И, наоборот, при захвате нуклона ядерные силы совершают положительную работу. За счет этой работы ядро получает дополнительную энергию и может испускать g-кванты.
Точно так же при переходе электрона с более высоких «боровских» орбит на более низкие в атоме водорода освобождается энергия, за счет которой испускаются фотоны. Разница здесь только в количестве выделенной энергии: энергия g-кванта примерно в 105–106 раз превосходит энергию фотонов видимого света.
Назовем энергией связи атомного ядра работу, которую необходимо совершить внешним силам, чтобы удалить друг от друга все нуклоны, составляющие ядро, на бесконечно большое расстояние.
А удельной энергией связи назовем отношение энергии связи ядра данного изотопа к числу нуклонов в его ядре:
Еуд = Есв/А, (26.2)
где А – массовое число изотопа.
Читатель: Тогда получается, что энергия двух отдельных нуклонов, протона и нейтрона будет больше, чем энергия ядра 1Н2 – ядра дейтерия? Ведь чтобы «растащить» это ядро на протон и нейтрон, придется совершить положительную работу.
Автор: Совершенно верно! Энергия отдельных нуклонов больше энергии ядра, составленного из эти нуклонов на величину энергии связи.
Читатель: Но тогда, если формула Эйнштейна (26.1) верна в данном случае, то масса ядра должна быть меньше суммы масс со-
| Таблица 26.1 Массы основных элементарных частиц | |
| Частица | т, а.е.м. |
| Электрон Протон Нейтрон | 0,00055 1,00728 1,00866 |
ставляющих его нуклонов на Есв/с2.
Автор: Так оно и есть! И это подтверждено многочисленными экспериментами. Значения масс (в атомных единицах массы) для основных элементарных частиц приведены в табл. 26.1, а для некоторых изотопов – в табл. 26.2.
Давайте убедимся, что масса ядра дейтерия действительно меньше суммарной массы протона и нейтрона.
Таблица 26.2
Дата добавления: 2016-04-11; просмотров: 2059;
