Полного внутреннего отражения?

Для луча, падающего на границу раздела среда–вакуум, спра­ведлива формула 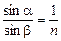, где п – абсолютный показатель пре­ломления среды. При падении луча на границу раздела под предель­ным углом a_пр угол преломления b = 90^о. Тогда:

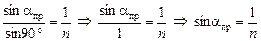Þ

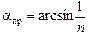. (4.7)

При углах падения a > a_пр преломленного луча просто не существует, то есть все лучи, падающие на границу раздела среда–вакуум с угла­ми падения a > a_пр полностью отражаются обратно. Поэтому-то за границей светлого пятна на воде поверхность воды совершенно тем­ная.

Задача 4.10.Вычислите предельный угол полного внутреннего отражения для грани­цы сероуглерод-воздух.

Решение. Абсолютный показатель преломления сероуглерода (табл. 4.1): п = 1,63. Согласно формуле (4.7)

= .

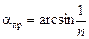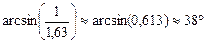Ответ: 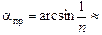38^о.

СТОП! Решите самостоятельно: А21–А24, В30–В32, С16, С19.

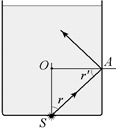Рис. 4.13

Задача 4.11. Прямоугольный стеклянный сосуд наполнен жидкостью и освещается снизу лампочкой, расположенной под сосудом вблизи дна (рис. 4.13). Каково минимальное значение абсолютного показателя преломления жидкости п_мин, при котором лампочку нельзя увидеть сквозь боковые стенки сосуда? Известно, что абсолютный показатель преломления стекла больше абсолютного показателя преломления жидкости.

Решение. Лампочку нельзя увидеть сквозь боковые стенки сосуда в том случае, когда все лучи от лампочки, падающие на эти стенки, испытывают полное внутреннее отражение.

Полное внутреннее отражение при условии, что стекло имеет бóльшую оптическую плотность, чем жидкость, луч может испытать только на границе «стекло–воздух».

Читатель: Но мы же ничего не знаем о показателе преломления стекла!

Автор: В данной задаче он нам не понадобится. Заметим, что стекло представляет собой тонкую плоскопараллельную пластинку. Пусть абсолютный показатель преломления стекла равен п_ст, а жидкости п_ж, по условию п_ст > п_ж.

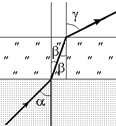Рис. 4.14

Рассмотрим луч, падающий на стекло из жидкости под углом a (рис. 4.14). Пусть угол преломления на границе «жидкость–стекло» равен b. Тогда, как видно из рисунка, этот же угол b будет углом падения на границе «стекло–воздух». И пусть угол преломления на границе «стекло–воздух» равен g. Тогда для границы «жидкость–стекло» справедливо

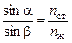. (1)

Для границы «стекло–воздух» справедливо

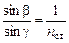. (2)

Перемножив почленно равенства (1) и (2), получаем

.

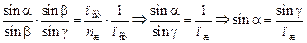При полном внутреннем отражении

g₀ = 90° Þ sing₀ = 1 Þ sina₀ = .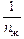

То есть угол полного внутреннего отражения на границе «стекло–воздух» будет точно таким же, как если бы никакого стекла вообще не было, а луч шел бы непосредственно из жидкости в воздух.

Заметим, что при обратном ходе луча из воздуха в жидкость можно точно так же вообще не рассматривать стекло, а считать, что преломление происходит непосредственно на границе «воздух–жидкость».

Вернемся к задаче. Условие полного внутреннего отражения на боковой стенке (см. рис. 4.13) имеет вид

,

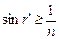где п – показатель преломления жидкости, а r¢ – угол падения луча на боковую стенку. Рассмотрим теперь лучи от источника S, проникающие в жидкость через дно сосуда. Поскольку жидкость по сравнению с воздухом является средой оптически более плотной, угол преломления лучей r не может быть больше некоторого предельного угла r₀, соответствующего скользящему падению луча от источника на дно сосуда. Предельный угол r₀ определяется из условия .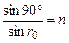

Из DSOA следует, что r¢ = 90° – r. Предельному углу r₀ соответствует минимальное значение угла падения лучей 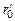на боковую грань, равное 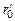= 90° – r₀.

Ясно, что все остальные лучи, попадающие в жидкость из точки S, будут образовывать с нормалью к нижней грани сосуда углы, меньшие, чем r₀ (см. рис. 4.13), а значит, на боковую грань они будут падать под углом, бóльшим, чем 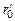= 90° – r₀. Поэтому если луч, упавший на боковую грань под углом 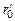, испытает полное внутреннее отражение от границы «стекло–воздух», то и все остальные лучи от источника S также испытают полное внутреннее отражение на этой границе.

Итак, мы имеем: 1) условие полного внутреннего отражение на боковой грани:

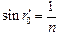, (1)

2) связь между углами r₀ и :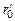

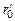= 90° – r₀, (2)

3) закон преломления «скользящего» луча, падающего от источника на нижнюю грань сосуда:

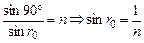. (3)

Подставляя (2) в (3), получим

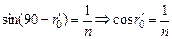. (4)

Используя основное тригонометрическое тождество, из (4) получим

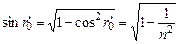. (5)

Подставляя (5) в (1), получим

,

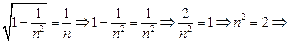
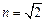то есть свет не выйдет через боковую грань, если абсолютный показатель жидкости будет равен .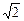

Читатель: Но нам надо найти минимальное значение п!

Автор: Найденное нами значение п = 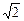и есть минимальное! В самом деле, мы установили, что при п = 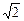ни один луч от лампочки через боковую стенку не выйдет. Если мы возьмем жидкость с абсолютным показателем преломления п > 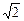, то максимально возможный угол r₀ (см. рис. 4.13) станет меньше, а угол падения на боковую стенку 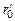– больше. Ясно, что в этом случае также будет происходить полное внутреннее отражение на боковой стенке.

Ответ: п_мин = .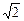

СТОП! Решите самостоятельно: С17, С18, D1.

Задача 4.12. В жидкости с показателем преломления п = 1,8 помещен точечный источник света. На каком максимальном расстоянии h над источником надо поместить диск диаметром D = = 2,0 см, чтобы свет не вышел из жидкости в воздух?

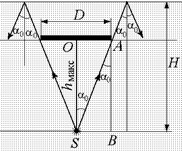Рис. 4.15

предельному углу падения a₀:

.

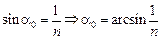С другой стороны, из DSOA следует

,

=

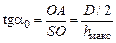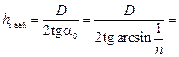
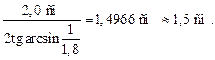
Читатель: В нашем случае диск расположен внутри жидкости, то есть глубина погружения источника Н > h_макс. А если Н < h_макс?

Автор: В этом случае, если диск расположить на поверхности жидкости, то все лучи, падающие на поверхность жидкости, будут иметь углы падения, большие 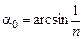. Поэтому в этом случае искомая величина h_макс будет равна глубине водоема.

Ответ: а) 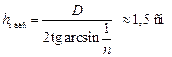, если глубина погружения источника больше 1,5 см; б) на поверхности, если глубина погружения меньше 1,5 см.

СТОП! Решите самостоятельно: С21, С22.

Задача 4.13. Каким должен быть внешний радиус изгиба световода, сделанного из прозрачного вещества с показателем преломления п = 4/3, чтобы при диаметре световода, равном d = 1 мм, свет, вошедший в световод перпендикулярно плоскости сечения (рис. 4.16), распространялся, не выходя наружу через боковую поверхность?

п = 4/3 d = 1 мм	Рис. 4.16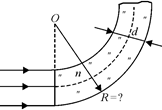
R = ?

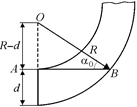Рис. 4.17

Решение. Луч АВ (рис. 4.17) образует наименьший угол падения a₀ на внешнюю поверхность. Условие невыхода света: угол a₀ больше предельного угла полного внутреннего отражения, т.е. .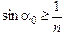

Из DОАВ имеем: 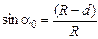, откуда

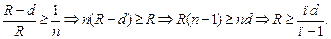
Подставим численные значения:

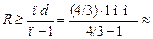4 мм.

Ответ: 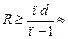4 мм.

СТОП! Решите самостоятельно: С20, D2, D3.

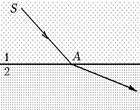Рис. 4.18