Как преломляется луч, падающий из среды
на границу с вакуумом?
Пусть луч падает из вакуума на границу раздела с прозрачной средой, абсолютный показатель преломления которой равен п, под углом i и преломляется под утлом i¢ (рис. 4.7, а).
Тогда справедлива формула:
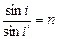 . (1)
. (1)
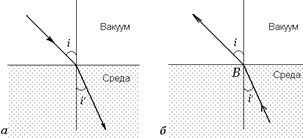
Рис. 4.7
Воспользуемся принципом обратимости световых лучей для того, чтобы определить показатель преломления вакуума относительно среды. Пустим луч из среды в вакуум в обратном направлении так, чтобы угол i¢ был углом падения. Так как траектория света при движении в обратном направлении не меняется, то i будет углом преломления.
Если обозначать угол падения буквойa, а угол преломления – буквой b, то в данном случае a = i¢ , b = i. Тогда
 , (2)
, (2)
где п¢ – искомый показатель преломления вакуума относительно среды. Перемножим почленно равенства (1) и (2) и получим
 .
.
Если вернуться к привычным нам обозначениям (a – угол падения, b – угол преломления), то при падении луча, идущего из среды на границу с вакуумом, справедливо
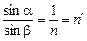 , (4.3)
, (4.3)
Задача 4.5.Световой луч падает на границу с вакуумом из воды (рис. 4.8, а) и из стекла (рис. 4.8, б). Постройте примерный ход преломленных лучей с учетом показателей преломления. Показатель преломления для воды п = 1,33, для стекла п = 1,6.

а б
Рис. 4.8
Решение. Согласно формуле (4.3) 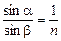 . Отсюда
. Отсюда 
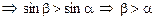 . То есть угол преломления в обоих случаях будет больше угла падения. При этом в случае б угол преломления будет больше, чем в случае а, так как у стекла абсолютный показатель преломления больше, чем у воды. Ход лучей показан на рис. 4.9.
. То есть угол преломления в обоих случаях будет больше угла падения. При этом в случае б угол преломления будет больше, чем в случае а, так как у стекла абсолютный показатель преломления больше, чем у воды. Ход лучей показан на рис. 4.9.

а б
Рис. 4.9
СТОП! Решите самостоятельно: А8–А10, В11–В13.
Задача 4.6.Луч света идет из глицерина в вакуум. Угол паденияa= 30о. Определите угол преломления.
| a = 30о | Решение. Из табл. 4.1 находим абсолютный показатель преломления глицерина: п = 1,47. Согласно формуле (4.3) |
| b = ? |

Подставим численные значения:
 .
.
Ответ: 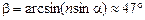 .
.
СТОП! Решите самостоятельно: А11, А12, В14, С4, С5.
Как преломляется луч на границе двух прозрачных сред
с абсолютными показателями преломления п1 и п2?
Договоримся первой средой называть ту, из которой идет луч, а второй средой — ту, в которую идет луч.
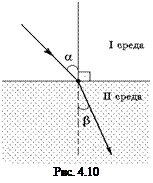 Пусть луч падает на границу первой и второй сред под некоторым углом a (рис. 4.10). Экспериментально установлено, что в этом случае справедливо соотношение:
Пусть луч падает на границу первой и второй сред под некоторым углом a (рис. 4.10). Экспериментально установлено, что в этом случае справедливо соотношение:
 , (4.4)
, (4.4)
где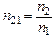 – относительный показатель преломления второй среды (т.е. той в которую идет луч) относительно первой (т.е. той, из которой идет луч). Заметим, что величина п может быть как больше, так и меньше единицы.
– относительный показатель преломления второй среды (т.е. той в которую идет луч) относительно первой (т.е. той, из которой идет луч). Заметим, что величина п может быть как больше, так и меньше единицы.
Отметим еще один важный экспериментальный факт: если свет идет из среды с абсолютным показателем преломления п1 в среду с абсолютным показателем преломления п2, то при п1 » п2 на границе между средами свет почти не отражается.
Если же, напротив, п1 и п2 существенно различаются, то значительная часть световой энергии на границе раздела сред отражается обратно.
СТОП! Решите самостоятельно: А13–А16, В16, С6–С8.
Задача 4.7.Свет падает из стекла (тяжелый флинт) в жидкий водород под некоторым углом. Известно, что угол преломления b = 60о. Определите угол падения.
| b = 60о | Решение. Из табл. 4.1 находим абсолютные показатели преломления для первой среды, из которой идет свет, – стекла (тяжелый флинт) п1= 1,80 и для второй среды, в которую идет свет, – жидкий водород п2 = 1,12. |
| a = ? | |
Согласно формуле (4.4):
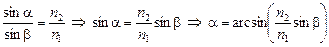 .
.
Подставим численные значения:
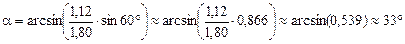 .
.
Ответ: 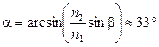 .
.
СТОП! Решите самостоятельно: А17, А18, В18–В21, С10, С11.
Дата добавления: 2016-04-11; просмотров: 2128;
