Закон преломления света
Преломление света на плоской границе
Что происходит с лучом света, падающим на границу раздела двух прозрачных сред, например, воздуха и воды?
Как мы знаем, часть световой энергии отражается от поверхности раздела, а часть проходит внутрь. При этом направление падающего луча определенным образом меняется. Например, при падении луча из воздуха на стеклянную пластину луч пойдет так, как показано на рис. 4.1.
| Изменение направления световых лучей при переходе из одной прозрачной среды в другую называется преломлением света. А угол, который луч, пересекший границу раздела сред, составляет с перпендикуляром, восстановленным к границе раздела сред, называется углом преломления. На рис. 4.1 a – это угол падения, а b – это угол преломления. Из рисунка видно, что угол падения явно не равен углу | 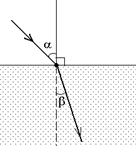 Рис. 4.1
Рис. 4.1
| 1 2 |
преломления. Возникает вопрос: какая существует зависимость между углом падения a и углом преломления b? Над этим вопросом думали ученые еще в античные времена, но впервые закон преломления света был сформулирован голландским физиком Виллебрордом Снеллиусом (1580–1626).
Закон преломления света
Падающий луч, преломленный луч и перпендикуляр, восстановленной к границе раздела двух сред в точке падения луча, лежат в одной плоскости, при этом выполняется соотношение:
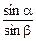 = п21, (4.1)
= п21, (4.1)
где a– угол падения; b – угол преломления; п21 – показатель преломления второй среды относительно первой.
В случае, когда свет падает из вакуума на какое-либо прозрачное вещество, величина п21 называется показателем преломления среды относительно вакуума или абсолютным показателем преломления.
В дальнейшем абсолютный показатель преломления будем обозначать буквой п без индексов.
В табл. 4.1 приведены абсолютные показатели преломления различных веществ.
Т а б л и ц а 4.1
| Вещество | п | Вещество | п |
| Воздух при нормальных условиях | 1,003 | Бензол | 1,5 |
| Жидкий гелий | 1,028 | Сахар | 1,56 |
| Жидкий водород | 1,12 | Стекло (легкий крон) | 1,57 |
| Лед | 1,31 | Сероуглерод | 1,63 |
| Вода | 1,33 | Рубин | 1,76 |
| Спирт этиловый | 1,36 | Стекло (тяжелый флинт) | 1,80 |
| Глицерин | 1,47 | Алмаз | 2,42 |
Заметим, что для всех прозрачных веществ величина абсолютного показателя преломления больше единицы. Из формулы (4.1) следует, что для луча света, падающего из вакуума в прозрачную среду, справедливо
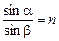 . (4.2)
. (4.2)
Отсюда следует, что 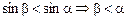 , то есть когда луч света попадает из вакуума в какое-либо прозрачное вещество, угол преломления всегда меньше угла падения, причем угол преломления будет тем меньше, чем больше абсолютный показатель преломленияп.
, то есть когда луч света попадает из вакуума в какое-либо прозрачное вещество, угол преломления всегда меньше угла падения, причем угол преломления будет тем меньше, чем больше абсолютный показатель преломленияп.
СТОП! Решите самостоятельно: А1, А2, В1, В2.
Задача 4.1.Постройте примерный ход преломленного луча по данному падающему лучу (рис. 4.2) с учетом показателей преломления веществ.
а 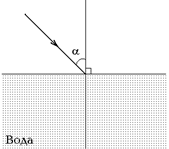
| б 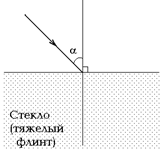
|
Рис. 4.2
Решение.
1. В обоих случаях угол преломления меньше угла падения: b < a.
2. Так как для стекла п = 1,8, а для воды п = 1,33, то в случае на рис. 4.3, б угол преломления будет меньше, чем в случае на рис. 4.3, а.
а 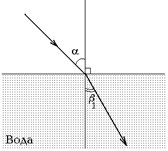
| б 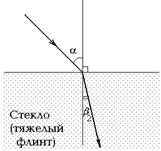
|
Рис. 4.3
СТОП! Решите самостоятельно: А3, А4, В3.
В дальнейшем, если не оговорено особо, во всех задачах будем считать, что для воздуха п = 1, т.е. не будем делать разницы между воздухом и вакуумом.
Задача 4.2.Луч света падает из воздуха на грань алмаза под некоторым углом. Определите угол падения, если угол преломления оказался равным b = 20о.
| b = 20о | Решение. Из табл. 4.1 находим значение абсолютного показателя преломления алмаза: п = 2,42. |
| a = ? |
Согласно формуле (4.1) 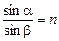 . Отсюда
. Отсюда
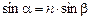 Þ
Þ 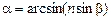 .
.
Подставим численные значения:
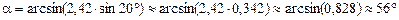 .
.
Ответ: 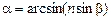 » 56о.
» 56о.
СТОП! Решите самостоятельно: А5, А6, В4–В6.
Задача 4.3. Под каким углом должен падать луч на поверхность стекла, чтобы угол преломления был в 2 раза меньше угла падения? Луч падает из вакуума, п = 1,6.
| п = 1,6 a = 2b | Решение. Согласно закону преломления
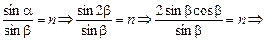
|
| a = ? |
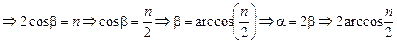 .
.
Подставим численные значения
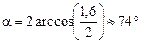 .
.
Ответ: 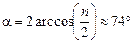 .
.
СТОП! Решите самостоятельно: В7–В9, С1.
Задача 4.4. На поверхности водоема, имеющего глубину Н = = 5,3 м, плавает фанерный круг радиусом r = 1,0 м, над центром которого на некоторой высоте расположен точечный источник света (рис. 4.4). Какова должна быть эта высота h, чтобы радиус R тени от круга на дне водоема был максимальным? Найти этот максимальный радиус. Показатель преломления воды п = 1,33.
| Н = 5,3 м п = 1,33 r = 1,0 м | Решение. Читатель: По-моему, радиус тени R будет максимален, когда угол преломления b будет максимален. |
| h = ? R = ? |
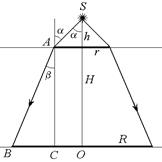 Рис. 4.4
Рис. 4.4
|
Автор: Верно. А из закона преломления следует, что b будет максимален тогда, когда максимален угол падения a. Кстати, каково максимально возможное значение a?
Читатель: Я думаю, 90°. То есть падающий луч должен идти как бы по касательной к поверхности воды.
Автор: Вы правы. А на какой же высоте h надо расположить источник света S, чтобы луч, идущий от него к краю фанерного круга, шел по направлению к поверхности воды?
Читатель: Наверное, h = 0.
Автор: Да. Значит, на первый вопрос задачи мы уже ответили. Теперь найдем радиус тени R, считая угол падения a = 90°.
Читатель: 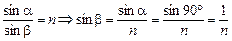 . Из DАВС (см. рис. 4.4) находим: R = BC + CO = Htgb + r. Поскольку
. Из DАВС (см. рис. 4.4) находим: R = BC + CO = Htgb + r. Поскольку 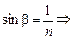
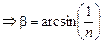 , то получаем окончательно
, то получаем окончательно
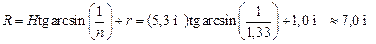 .
.
Ответ: h = 0; 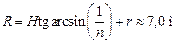 .
.
СТОП! Решите самостоятельно: В10, С2, С3.
Дата добавления: 2016-04-11; просмотров: 3468;
