Экспериментальные факты

Рис. 11.1

1. Если катушку, состоящую из большого числа витков проволоки, быстро надевать на магнит или сдергивать с него, то в ней возникает кратковременный ток, называемый индукционным. То же происходит, если магнит быстро вдвигать в катушку или выдвигать из нее.

На рис. 11.1 показано, как при относительном перемещении катушки и магнита в катушке возникает индукционный ток: а – катушка надевается на магнит, б – магнит вдвигается в катушку.

Индукционный ток прекращается, как только прекращается относительное движение магнита и катушки.

Чтобы детально разобраться с данным явлением, рассмотрим серию опытов.

Первая серия опытов: изменение магнитной индукции поля, в котором находится индукционный контур (катушка или рамка).

Катушка помещена в магнитное поле, например внутрь соленоида (рис. 11.2, а)или между полюсами электромагнита (рис. 11.2, б).

Рис. 11.2

Установим катушку так, чтобы плоскость ее витков была перпендикулярна к линиям магнитного поля соленоида или электромагнита. Будем изменять магнитную индукцию поля, быстро изменяя силу тока в обмотке (спомощью реостата) или просто выключая и включая ток (ключом). При каждом изменении магнитного поля стрелка гальванометра дает резкий отброс; это указывает на возникновение в цепи катушки индукционного электрического тока. При усилении (или возникновении) магнитного поля возникнет ток одного направления, при его ослабления (или исчезновении) – обратного.

Рис. 11.3

Проделаем теперь тот же опыт, установив катушку так, чтобы плоскость ее вит­ков была параллельна направлению линий магнитного поля (рис. 11.3). Опыт даст отрицательный результат: как бы мы ни изменяли магнитную индукцию поля, мы не обнаружим в цепи катушки индукционного тока.

Вторая серия опытов: изменение положения катушки, находящейся в неизменном магнитном поле.

Рис. 11.4

Поместим катушку внутрь соленоида, где магнитное поле однородно, и будем быстро поворачивать ее на некоторый угол вокруг оси, перпендикулярной к направлению поля (рис. 11.4, б). При всяком таком повороте гальванометр, соединенный с катушкой, обнаруживает индукционный ток, направление которого зависит от начального положения катушки и от направления вращения. При полном оборо­те катушки на 360° направление индукционного тока изме­няется дважды: всякий раз, когда катушка проходит положение, при котором плоскость ее перпендикулярна к направлению магнитного поля.

Если, однако, перемещать катушку так, чтобы она не поворачивалась относительно направления поля, а лишь перемещалась параллельно самой себе в любом направле­нии вдоль поля, поперек его или под каким-либо углом к направлению поля, то индукционный ток возникать не будет.

Если поле неод­нородно (например, вблизи полюса магнита или электромагнита), то всякое перемещение катушки может сопровождаться появлением индукционного тока, за исключением одного случая: индукционный ток не возникает, если катушка движется так, что плоскость ее все время остается параллельной направлению поля (т. е. сквозь катушку не прохо­дят линии магнитного поля).

Третья серия опытов: изменение площади контура, находящегося в неизменном магнитном поле.

Подобный опыт можно осуществить по следующей схеме (рис. 11.5). В магнитном поле, например между полюсами большого электромагнита, поместим контур, сделанный из гибкого провода. Пусть первоначально контур имел форму окружности (рис. 11.5, а). Быстрым движением руки можно стянуть контур в узкую петлю, значительно уменьшив таким образом охватываемую им площадь (рис. 11.5, б). Гальванометр покажет при этом возникновение индукционного тока.

Рис. 11.5

Еще удобнее осуществление опыта с изменением площади контура по схеме, изображенной на рис. 11.6.

Рис. 11.6

В магнитном поле расположен контур abсd, одна из сторон которого (bс на рис. 11.6) сделана подвижной. При каждом ее передвижении гальванометр обнаруживает возникновение в контуре индукционного тока. При этом при передвижении bс влево (увеличение площади abсd)индукционный ток имеет одно направление, а при передвижении bс вправо (уменьшение площади abсd)– противоположное. Однако и в этом случае изменение площади контура не дает никакого индукционного тока, если плоскость контура параллельна направлению магнитного поля.

Сопоставляя все описанные опыты, мы можем сформулировать условия возникновения индукционного тока в общей форме. Во всех рассмотренных случаях мы имели контур,помещенный в магнитное поле, причем плоскость контура могласоставлять тот или иной угол с направлением маг­нитной индукции. Обозначим площадь, ограниченную кон­туром, через S, магнитную индукцию поля через 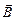,а угол между направлением магнитной индукции и нормалью к контуру через j. В таком случае составляющая магнитной индукции, перпендикулярная к пло­скости контура, будет равна по мо­дулю (рис. 11.7)

Рис. 11.7

В_^ = Вcosj.

Произведение B_^S мы будем назы­вать потоком магнитной индукции или, короче, магнитным потоком через контур; эту величину мы будем обозначать буквой Ф. Таким образом,

Ф = B_^S = ВScosj. (11.1)

В системе СИ магнитный поток измеряется в веберах[2] (Вб). Один вебер представляет собой поток через поверхность, площадь которой равна одному квадратному метру, пересекаемую перпендикулярными к ней линиями однородного поля с магнитной индукцией, равной одному тесла:

1 Вб = 1 Тл × 1 м².

Во всех рассмот­ренных случаях индукционный ток возникал тогда, когда мы тем или иным способом изменяли магнитный поток Ф. В одних случаях мы осуществля­ли это путем изменения магнитной индукции В (см. рис. 11.2); в других – изменяли угол j (см. рис. 11.4);в третьих – площадь S (рис. 11.5). В об­щем случае, конечно, возможно одновременное изменение всех этих величин, определяющих магнитный поток через контур. Внимательное рассмотрение самых разнообразных индукционных опытов, показывает, что индукционный ток возникает тогда и только тогда, когда изменяется магнитный поток Ф; индукционный ток никогда не возникает, если магнитный поток Ф через данный контур остается неизменным.

Итак: при всяком изменении магнитного потока через проводящий контур в этом контуре возникает электрический ток.

В этом и заключается один из важнейших законов природы – закон электромагнитной индукции, открытый Фарадеем[3] в 1831 г.

Задача 11.1. Вычислите магнитный поток через рамку площадью S = 100 см², если магнитная индукция В = 2,0 Тл, а положение рамки показано на рис. 11.8.

В = 2,0 Тл S = 100 см2
Ф = ?
Рис. 11.8

Решение. Прежде всего, определим угол a, который вектор 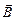составляет с нормалью 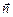к рамке: а) a = 0; б) a = 30°; в) a = 90°; г) a = 180°; д) a = 180 – 30 = 150°. Теперь воспользуемся формулой (11.1), получим:

а) Ф = BScosa = 2,0 Тл × 1,00×10^–2 м² × cos0 = 2,0×10^–2 Вб;

б) Ф = BScosa = 2,0 Тл × 1,00×10^–2 м² × cos30° » 1,7×10^–2 Вб;

в) Ф = BScosa = 2,0 Тл × 1,00×10^–2 м² × cos90° = 0;

г) Ф = BScosa = 2,0 Тл × 1,00×10^–2 м² × cos180° = –2,0×10^–2 Вб;

д) Ф = BScosa = 2,0 Тл × 1,00×10^–2 м² × cos150° = –1,7×10^–2 Вб.

Ответ: а) 2,0×10^–2 Вб; б) 1,7×10^–2 Вб; в) 0; г) –2,0×10^–2 Вб; д) –1,7×10^–2 Вб.

СТОП! Решите самостоятельно: А1–А3, В1.

Итак, для того чтобы в контуре возник индукционный ток, необходимо, чтобы изменялся магнитный поток, пронизывающий этот контур: Ф = BScosa.

А изменять магнитный поток можно одним из трех способов: 1) изменяя В; 2) изменяя S; 3) изменяя a. (Конечно, можно одновременно изменять все три величины или любые две из трех.)

Если все три величины (В, S, cosa) в опыте неизменны, то индукционный ток не возникает. Не возникает он и в том случае, если одна из этих величин равна нулю, а две другие как-то меняются. Например, если В = 0 (магнитное поле отсутствует), то как бы мы не крутили катушку, никакого тока в ней не возникнет. И если cosa = 0 (a = 90°, т.е. нормаль к рамке 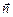перпендикулярна вектору 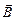), то как бы мы не изменяли величину В, индукционный ток не возникнет.

СТОП! Решите самостоятельно: А4–А7, В2, В3, С1–С3.

Правило Ленца[4]

 

Теперь попробуем разобраться, в каком направлении течет индукционный ток.

Для этого проследим внимательно за направлением тока в каком-нибудь индукционном опыте, например в опыте изображенном на рис. 11.2, а. Схема этого опыта показана на рис. 11.9, причем каждая из катушек I и II изображена виде одного витка, а стрелки I_перв и I_инд указывают соответственно направление первичного тока в катушке I и направление индукционного тока в катушке II.

Рис. 11.9

Рис. 11.9, а относится к случаю, когда ток I_перв усиливается, а рис. 11.9, б – к случаю, когда он ослабляется. Мы видим, что в первом случае, т. е. при усилении магнитного поля, и следовательно, при увеличении магнитного потока, токи в катушках I и II имеют противоположные направления; напротив, в случае, когда индукция происхо­дит вследствие ослабления магнитного поля, т. е. при умень­шении магнитного потока, оба тока I_перв и I_инд имеют одинаковые направления. Иначе можно сказать, что когда причиной индукции является усиление магнитного потока, пронизывающего площадь контура, то возникающий индук­ционный ток направлен так, что он ослабляет первоначаль­ный магнитный поток. Напротив, когда индукция происходит вследствие ослабления магнитного потока, магнитное поле индукционного тока усиливает первоначальный маг­нитный поток.

Полученный нами результат можно сформулировать в виде общего правила:

Индукционный ток всегда имеет такое направление, при котором его магнитное поле уменьшает (компенсирует) изменение магнитного потока, являющееся причиной возник­новения этого тока.

Рис. 11.10

Это общее правило соблюдается во всех без исключения случаях индукции. Рассмотрим, в частности, случай, когда индукция вызывается перемещением контура или части его относительно магнитного поля. Такой опыт изображен на рис. 11.1, а схема его показана на рис. 11.10, причем стрелки навитке указывают направление тока, индуцируемого в катушке при ее приближении к северному полюсу магнита N (рис. 11.10, а)или при ее удалении от этого полюса (рис. 11.10, б). Пользуясь правилом буравчика, легко определить направление магнитного поля индукционного тока и убедиться, что оно соответствует сформулированному выше правилу.

В самом деле, когда магнит движется вниз (см. рис. 11.10, а), магнитный поток в направлении «вниз» возрастает. Значит, индукционный ток в контуре должен создавать магнитное поле, ослабляющее этот поток, т.е. вектор 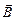поля контура должен быть направлен вверх. Зная направление 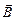, по правилу буравчика определяется направление тока в контуре.

Когда магнит движется вверх (см. рис. 11.10, б), магнитный поток в направлении «вниз» убывает. Значит, индукционный ток в контуре должен создавать магнитное поле, усиливающее этот поток, т.е. вектор 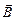поля контура должен быть направлен вниз. Зная направление 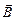, по правилу буравчика определяется направление индукционного тока.

Обратим теперь внимание на такой факт. Когда в катушке возникает индукционный ток, она становится эквивалентной магниту, положение северного и южного полюсов которого можно определить по правилу буравчика. На рис. 11.10 показано, что в случае а на верхнем конце катушки возникает северный полюс, а в случае б – южный полюс. Из этого рисунка мы видим, что когда мы приближаем к индукционной катушке, скажем, северный полюс магнита N, то на ближайшем к нему конце катушки возникает также северный полюс, а когда мы удаляем от катушки северный полюс магнита, то на ближайшем конце катушки возникает южный полюс. Но, как мы знаем, магниты, обращенные друг к другу одноименными полюсами, отталкиваются, а разноименными – притягиваются. Поэтому, когда индукция происходит вследствие приближения магнита к катушке, то силы взаимодействия между магнитом и индукционным током отталкивают магнит от катушки, а когда индукция происходит при удалении магнита от катушки, то они притягиваются друг к другу. Таким образом, для случаев, когда индукция происходит вследствие движения магнита или всего индукционного контура в целом, мы можем установить следующее общее правило, по существу равносильное правилу, сформулированному выше, но для этих случаев более удобное:

Индукционный ток всегда имеет такое направление, что взаимодействие его с первичным магнитным полем противодействует тому движению, вследствие которого происходите индукция.

Это правило носит название правила Ленца.

Правило Ленца стоит в тесной связи с законом сохранения энергии. В самом деле, представим себе, например, что при приближении север­ного полюса магнита N к соленоиду ток в нем имел бы направление, про­тивоположное тому, какого требует правило Ленца, т. е. что на ближай­шем к магниту конце соленоида возникал бы не северный, а южный по­люс. В этом случае между соленоидом и магнитом возникли бы не силы отталкивания, а силы притяжения. Магнит продолжал бы самопроиз­вольно и со все большей скоростью приближаться к соленоиду, созда­вая в нем все большие индукционные токи и тем самым все более уве­личивая силу, притягивающую его к соленоиду. Таким образом, без всякой затраты внешней работы мы получили бы, с одной стороны, не­прерывное ускоренное движение магнита к соленоиду, а с другой, все более возрастающий ток в соленоиде, способный производить работу. Ясно, что это невозможно и что индукционный ток не может иметь дру­гого направления, чем то, которое указывается правилом Ленца. В том же можно убедиться, рассматривая и другие случаи индукции.

Рис. 11.11

На рис. 11.11 показан очень простой и наглядный опыт, иллюстрирующий правило Ленца. Алюминиевое кольцо, служащее индукционной катушкой, подвешено вблизи полюсов сильного магнита или электромагнита, который можно передвигать по рельсу. Отодвигая магнит от кольца, увидим, что кольцо следует за ним. Напротив, придвигая магнит к кольцу, обнаружим, что кольцо уходит от магни­та. В обоих случаях при движении магнита изменяется магнитный поток сквозь кольцо, и в кольце возникает ин­дукционный ток. По правилу Ленца этот ток направлен так, что взаимодействие его сперемещающимся магнитом тормозит движение магнита; согласно третьему закону Ньютона силы противодействия приложены к кольцу и вызывают его перемещение.

СТОП! Решите самостоятельно: А8, А9, В4–В6, С4, С5.

<3456789>

---

Дата добавления: 2016-04-11; просмотров: 1551;

---