Поле кругового тока
Попробуем, используя закон Биó–Савара–Лапласа, вычислить значение вектора В в центре кругового витка провода радиусом R. по которому течет ток I (рис. 10.7).
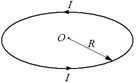 Рис. 10.7
Рис. 10.7
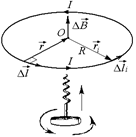 Рис. 10.8
Рис. 10.8
|
Рассмотрим малый участок проводника длиной Dl (рис. 10.8). Согласно формуле (10.2) он создает в центре кольца индукцию
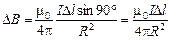 .
.
Если вращать буравчик так, чтобы его ручка поворачивалась из положения, совпадающего с вектором 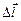 , в положение, совпадающее с вектором
, в положение, совпадающее с вектором 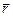 , то буравчик будет двигаться вверх, поэтому вектор
, то буравчик будет двигаться вверх, поэтому вектор 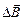 направлен вверх.
направлен вверх.
Поскольку в силу симметрии задачи любой участок провода с током такой же длины создает в точке О точно такое же поле 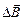 , то легко найти результирующее значение вектора
, то легко найти результирующее значение вектора 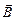 в точке О, разбив это кольцо с током на N одинаковых элементов тока
в точке О, разбив это кольцо с током на N одинаковых элементов тока 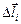 и просуммировав значения DBi, созданные каждым из этих элементов:
и просуммировав значения DBi, созданные каждым из этих элементов:
 .
.
Запомним: вектор магнитной индукции в центре кругового тока равен
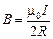 . (10.3)
. (10.3)
Поле прямого тока
 Рис. 10.9
Рис. 10.9
|
Пусть по прямому бесконечному проводу течет ток I. Требуется вычислить вектор магнитной индукции 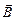 на расстоянии d от провода (рис. 10.9).
на расстоянии d от провода (рис. 10.9).
Мы уже знаем, что линии магнитной индукции прямого тока имеют вид концентрических окружностей, а направление вектора 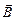 проще всего определить с помощью правила правого кулака.
проще всего определить с помощью правила правого кулака.
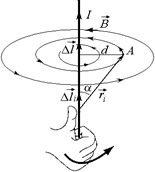 Рис. 10.10
Рис. 10.10
|
Рассмотрим произвольную точку А (рис. 10.10). Каждый элемент тока Dli создает в точке А индукцию 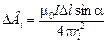 , направленную «от нас». Чтобы найти результирующее значение В, надо просуммировать все DBi.
, направленную «от нас». Чтобы найти результирующее значение В, надо просуммировать все DBi.
Заметим, что в данном случае число элементов тока Dli бесконечно, так как прямая бесконечна. Поэтому подобное суммирование требует уверенного владения методами интегрирования. Если вы уже хорошо владеете высшей математикой, попробуйте самостоятельно вычислить значение В. Мы же ограничимся тем, что приведем окончательный ответ:
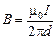 . (10.4)
. (10.4)
| Задача 10.2. Вычислите значение магнитной индукции В в точке О (рис. 10.11). Величины I и R заданы. | 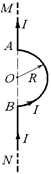 Рис. 10.11
Рис. 10.11
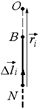 Рис. 10.12
Рис. 10.12
|
| I R | Решение. Вычислим значение 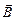 как суперпозицию полей полуокружности и двух лучей АМ и ВN.
1. Индукция поля, созданного током, теку- как суперпозицию полей полуокружности и двух лучей АМ и ВN.
1. Индукция поля, созданного током, теку-
|
| B | |
щим по половине окружности, равна половине индукции поля, созданного полем, текущим по окружности (формула (10.3)):
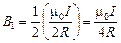 .
2. Рассмотрим произвольный элемент тока .
2. Рассмотрим произвольный элемент тока 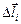 на луче NB (рис. 10.12). Проведем из начала вектора на луче NB (рис. 10.12). Проведем из начала вектора 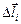 радиус-вектор радиус-вектор 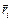 в точку О.
Ясно, что угол a между векторами в точку О.
Ясно, что угол a между векторами 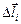 и и 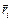 равен 0, поэтому индукция DBi, созданная этим полем, согласно (10.2) равна равен 0, поэтому индукция DBi, созданная этим полем, согласно (10.2) равна
|
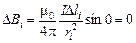 .
.
Значит, и результирующее поле, созданное током каждого из лучей АМ и NB, равно нулю. Следовательно, результирующим полем будет поле, созданное током полуокружности:
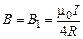 .
.
Ответ: 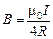 .
.
СТОП! Решите самостоятельно: В5, В6, С1, С2, D1, D2.
Дата добавления: 2016-04-11; просмотров: 1191;
