Созданного этим током?

Пусть по некоторому проводу произвольной формы течет ток I. Спрашивается, чему будет равна магнитная индукция поля, созданная этим током в произвольной точке А (рис. 10.2)?

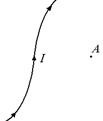Рис. 10.2 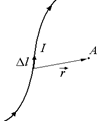Рис. 10.3

Попробуем свести эту задачу к более простой: чему равна индукция магнитного поля, созданного малым участком провода Dl, по которому течет ток I, в точке А, положение которой в пространстве задается вектором 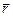(рис. 10.3)?

Если мы сумеем ответить на этот вопрос, то дальше, разбивая провод на маленькие участки Dl_i и используя принцип суперпозиции, мы сможем вычислить индукцию магнитного поля в точке А, созданного током во всем проводе.

В 1820 г. Био и Савар провели большое число экспериментов по измерению магнитной индукции полей, созданных проводниками с током различной формы. Проанализировав эти данные, Лаплас установил закон, который физики назвали законом Биó–Савара–Лапласа.

Пусть по малому участку провода, толщиной которого можно пренебречь, течет ток I. Пусть длина этого участка Dl, а положение в пространстве задается вектором 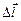(| | 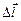= Dl) (рис. 10.4).

Рис. 10.4 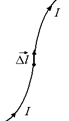Рис. 10.5.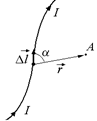

Проведем из начала вектора 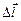в произвольную точку А пространства радиус-вектор 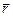, который составляет с вектором 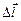угол a (рис. 10.5). Малый прямолинейный участок тока с заданным направлением 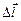будем в дальнейшем называть элементом тока.

Экспериментально установлено, что модуль вектора магнитной индукции 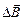поля, созданного участком провода 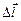, по которому течет ток I, равен

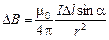, (10.2)

где m₀ = 4p×10^–7 (Тл×м)/А – экспериментально установленный коэффициент пропорциональности, который называется магнитной постоянной.

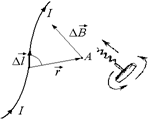Рис. 10.6

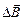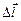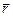Направлен вектор перпендикулярно плоскости, содержащей векторы и . Если вращать рукоятку буравчика от 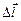к 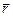в направлении наименьшего угла между этими векторами, то поступательное перемещение буравчика укажет направление вектора 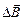. В случае, изображенном на рис. 10.6, вектор 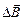направлен перпендикулярно чертежу «от нас».