Задачи с использованием
Телесного угла
Задача 5.1. Определить поток напряженности электрического поля точечного заряда q через поверхность S, которая видна из точки, где находится заряд, под телесным углом W (рис. 5.7).
| q S W |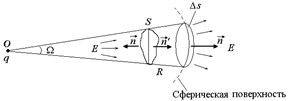 
Рис. 5.7
|
| Ф = ? | |
Решение. Пересечем этот телесный угол W, под которым видна поверхность S, сферой радиуса R так, чтобы получилась замкнутая поверхность, у которой нижнее «основание» – поверхность S(наша), а верхнее «основание» – сферическая поверхность радиуса R. Боковая поверхность образована лучами, исходящими из точки О.
Поток через эту поверхность Ф = 0, так как она не содержит зарядов, поэтому
0
Ф = ФповS + Фпов.сферы + Фбок = 0,
ФповS + Фпов.сферы = 0,
ФповS = – Фпов.сферы.
Здесь Фпов.сферы – поток в направлении из замкнутой поверхности. Интересующий же нас поток через S проходит в направлении нормали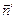 
:
Ф = –ФповS = + Фпов.сферы!
Полный поток через всю сферу радиуса R от заряда q по теореме Гаусса равен
Фполн =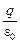 
.
Поскольку поле 
сферически симметрично, то поток через часть сферической поверхности, вырезанной нашим телесным углом, пропорционален площади этой поверхности:
| Фчасть сферы = Фчерез всю сферу × | Площадь части сферы | . |
| Площадь всей сферы |
.
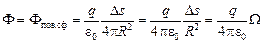Ответ: Ф =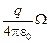 
.
Задача 5.2. Поток напряженности электрического поля через плоскую поверхность, равномерно заряженную с поверхностной плотностью заряда σ равен Ф. Чему равна электрическая сила, действующая на пластину в направлении, перпендикулярном ее плоскости?
| σ Ф | Решение. Разобьем нашу площадку на маленькие участки площадью Dsi каждый (рис. 5.8). Пусть напряженность поля в пределах площадки Dsi не меняется.
|
| F^ = ? |
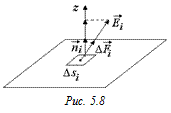Тогда сила, с которой поле действует на площадку Dsi, равна
.
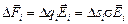Проекция этой силы на вертикальное к площадке направление оси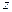 
равна
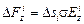
или (если ввести нормаль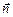 
)
.
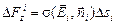Полная проекция силы на направление z равна сумме всех проекций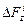 
:
.
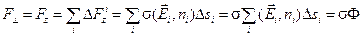Ответ: F^ = σФ.
Вывод: если мы узнаем σ и Ф, то мы узнаем нормальную составляющую силы!
F^ = σФ.
Задача 5.3. В центре куба, грани которого равномерно заряжены с поверхностной плотностью заряда σ, находится точечный заряд q (рис. 5.9). Найти силу, с которой он действует на одну из граней куба.
| σ q |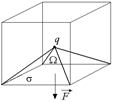 
Рис. 5.9
| Решение. Согласно решению задачи 5.2
 .
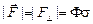Согласно решению задачи 5.1
 .
|
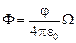| F = ? | ||
В силу симметрии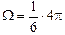 
. Тогда
.
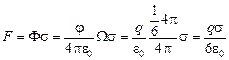Ответ: F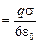 
.
СТОП! Решите самостоятельно: С6.
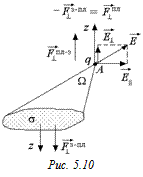
Задача 5.4. Плоская площадка равномерно заряжена с поверхностной плотностью заряда σ. Найти проекцию вектора напряженности поля на направление, нормальное к площадке, созданного площадкой в точке А, из которой данная площадка видна под телесным углом W.
| σ W | Решение. Поместим в точке А точечный заряд q (рис. 5.10). Тогда проекция силы на вертикальное к площадке направление, с которой заряд действует на площадку, равна |
| Е^ = ? | |
.
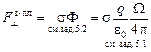По 3-му закону Ньютона площадка будет действовать на заряд в противоположном направлении с силой
.
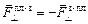Итак, на заряд со стороны площадки действует в вертикальном направлении сила
.
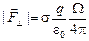Но, с другой стороны,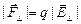 
, где Е^ – вертикальная составляющая напряженности поля, созданного площадкой. Отсюда
= 
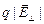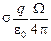Þ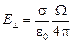 
.
Ответ: .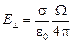
Задача 5.5. Найти напряженность электрического поля в центре куба, пять граней которого заряжены с поверхностной плотностью σ, а одна не заряжена.
| σ | Решение. Представим поле нашего куба как суперпозицию двух полей: 1) куба, у которого все грани заряжены с поверхностной плотностью заряда +σ; 2) одной грани с поверхностной плотностью заряда (–σ). |
| Е = ? | |
Напряженность поля, созданного кубом, у которого все грани заряжены, в силу симметрии равна нулю. Значит, достаточно вычислить напряженность только от одной грани:
.
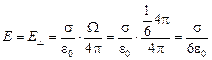(задача 5.4) (задача 5.3)
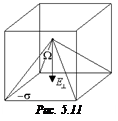
Причем направлена перпендикулярно к незаряженной грани (рис. 5.11).
Ответ: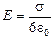 
.
СТОП! Решите самостоятельно: С3.
Дата добавления: 2016-04-11; просмотров: 5146;