Решение задач с помощью
Закона Гаусса
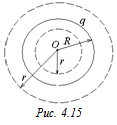
Задача 4.8. Определить напряженность поля равномерно заряженной сферы радиуса R и зарядом q > 0 на расстоянии r от центра сферы (рис. 4.15). Построить график |  |.
|.
 Решение. Рассмотрим два случая.
Решение. Рассмотрим два случая.
1. Пусть r < R. Возьмем сферу радиуса r с центром в точке О и вычислим поток вектора  через нее. Поскольку задача сферически симметрична, то вектор
через нее. Поскольку задача сферически симметрична, то вектор  должен быть направлен по радиусу и иметь одинаковую величину в каждой точке сферы:
должен быть направлен по радиусу и иметь одинаковую величину в каждой точке сферы:
Ф = 4pr2|  |.
|.
По закону Гаусса
Ф = (заряд внутри сферы)/e0.
Поскольку внутри сферы заряда нет, то
Ф = 0/e0 = 0.
Следовательно,
0 = 4pr2|  | Þ |
| Þ |  | = 0.
| = 0.
Итак, внутри равномерно заряженной сферы напряженность равна нулю!
2. Пусть r > R. Возьмем сферу радиуса r с центром в точке О. Тогда Ф = 4pr2|  |, по закону Гаусса
|, по закону Гаусса 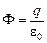 , отсюда
, отсюда
4pr2|  | =
| = 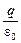 Þ
Þ 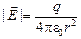 .
.
 Итак, поле вне равномерно заряженной сферы совпадает с полем точечного заряда, помещенного в центре сферы.
Итак, поле вне равномерно заряженной сферы совпадает с полем точечного заряда, помещенного в центре сферы.
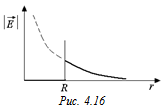
Построим график | 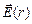 | (рис. 4.16).
| (рис. 4.16).
СТОП! Решите самостоятельно: А4, В5.
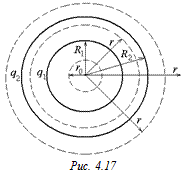
Задача 4.9. Поле создано двумя равномерно заряженными концентрическими сферами с радиусами R1 и R2 (рис. 4.17). Заряд внутренней сферы равен q1, а внешней q2. Построить график зависимости проекции вектора напряженности  на ось
на ось 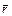 , проходящую через центр сфер для случаев: а) q1 > 0, q2 > 0; б) q1 > 0, q2 < 0, q1 = –q2; в) q1 > 0, q2 < 0, |q1| < |q2|; г) q1 < 0, q2 > 0, |q1| > |q2|. Графики строить только в области r > 0.
, проходящую через центр сфер для случаев: а) q1 > 0, q2 > 0; б) q1 > 0, q2 < 0, q1 = –q2; в) q1 > 0, q2 < 0, |q1| < |q2|; г) q1 < 0, q2 > 0, |q1| > |q2|. Графики строить только в области r > 0.
 Решение.
Решение.
1. 0 < r < R1. Возьмем сферу радиуса r. Тогда
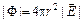 ,
, 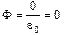 ,
,
|  | = 0, Еr = 0.
| = 0, Еr = 0.
2. R1 < r < R2. Возьмем сферу радиуса r. Поскольку задача сферически симметричная, то вектор  должен быть направлен вдоль радиуса сферы. При этом возможны два случая: либо
должен быть направлен вдоль радиуса сферы. При этом возможны два случая: либо 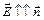 , либо
, либо 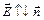 , где
, где 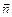 – внешняя нормаль к сфере.
– внешняя нормаль к сфере.
Проекция вектора  на ось r равна
на ось r равна
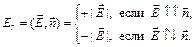
Тогда поток вектора  через сферу можно записать как
через сферу можно записать как 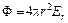 . По теореме Гаусса
. По теореме Гаусса 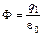 , отсюда
, отсюда
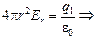
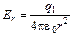 ,
,
где q1 берется с учетом знака.
3. r > R2. Тогда 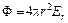 ,
, 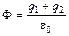 (заряды q1 и q2 берутся с учетом знака). Отсюда
(заряды q1 и q2 берутся с учетом знака). Отсюда
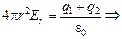
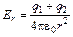 .
.
Построим графики Er(r) для случаев а)–г) (рис. 4.18).
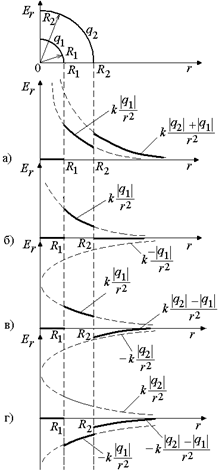
Рис. 4.18
СТОП! Решите самостоятельно: В6.
Задача 4.10. Определитьнапряженность поля равномерно заряженной бесконечной нити с линейной плотностью заряда l на расстоянии r от нее.
Решение. Поскольку задача имеет осевую симметрию, то вектор напряженности  (r)должен быть направлен перпендикулярно нити и иметь одинаковые значения во всех точках цилиндрической
(r)должен быть направлен перпендикулярно нити и иметь одинаковые значения во всех точках цилиндрической 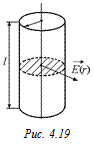 поверхности радиуса r, окружающей нить (рис. 4.19). Вычислим поток вектора
поверхности радиуса r, окружающей нить (рис. 4.19). Вычислим поток вектора  через цилиндр высотой l, окружающий нить.
через цилиндр высотой l, окружающий нить.
Отметим, что поскольку  перпендикулярен нити, то поток через верхнее и нижнее основания равен нулю. Поток через цилиндрическую поверхность равен
перпендикулярен нити, то поток через верхнее и нижнее основания равен нулю. Поток через цилиндрическую поверхность равен 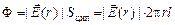 .
.
По закону Гаусса
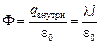 Þ
Þ 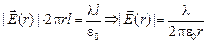 .
.
Ответ: 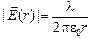 .
.
СТОП! Решите самостоятельно: С2.
Задача 4.11. Определить напряженность поля бесконечной равномерно заряженной плоскости с поверхностной плотностью заряда σна расстоянии r от нее (рис. 4.20).
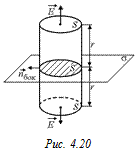 Решение. Возьмем цилиндр с площадью основания S и высотой 2r,среднее сечение которого лежит на заряженной плоскости. Вычислим поток вектора
Решение. Возьмем цилиндр с площадью основания S и высотой 2r,среднее сечение которого лежит на заряженной плоскости. Вычислим поток вектора 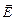 . Из соображений симметрии ясно, что
. Из соображений симметрии ясно, что  перпендикулярен плоскости, а значения |
перпендикулярен плоскости, а значения |  |на верхнем и нижнем основаниях цилиндра равны. Поток через боковую поверхность цилиндра равен нулю, так как
|на верхнем и нижнем основаниях цилиндра равны. Поток через боковую поверхность цилиндра равен нулю, так как 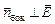 . Отсюда
. Отсюда
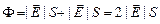 .
.
По закону Гаусса 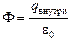 . Поскольку
. Поскольку 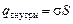 , получаем
, получаем
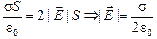 .
.
Ответ: 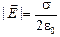 .
.
Отметим, что 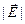 не зависит от расстояния до плоскости!
не зависит от расстояния до плоскости!
СТОП! Решите самостоятельно: А1, А2, А5.
Задача 4.12. Поле создано парой параллельных бесконечных равномерно заряженных плоскостей с плотностями зарядов: а) +σ и +σ; б) +σ и –σ. Определить напряженность поля между плоскостями и снаружи.
Решение. Изобразим векторы напряженности полей, создаваемых плоскостями 1 и 2 внутри и снаружи (рис. 4.21).
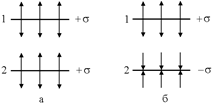 Рис. 4.21
Рис. 4.21
Согласно решению задачи 4.11 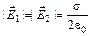 . Тогда:
. Тогда:
а) (рис. 4.21,а) внутри 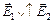 , снаружи
, снаружи 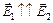 , следовательно,
, следовательно,
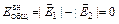 ;
;
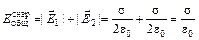 ;
;
б) (рис. 4.21,б) внутри 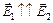 , снаружи
, снаружи 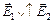 , следовательно,
, следовательно,
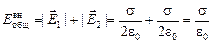 ;
;
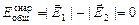 .
.
Ответ: а) 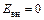 ,
, 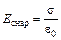 ; б)
; б) 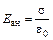 , Еснар = 0.
, Еснар = 0.
CТОП! Решите самостоятельно: А3, В2, С1.
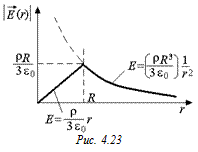
Задача 4.13. Определить напряженность равномерно объемно заряженного шара радиуса R с объемной плотностью заряда ρ на расстоянии r от центра шара (рис. 4.22). Построить график Е(r).
Решение. 1. Возьмем сферу радиуса r < R, тогда
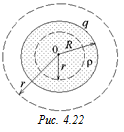
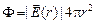 .
.
По закону Гаусса 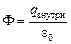 . Так как
. Так как
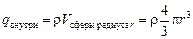 ,
,
то
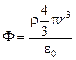 ;
;
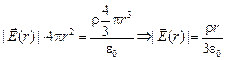 .
.
Таким образом, внутри шара 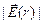 – линейная функция.
– линейная функция.
2. Возьмем сферу радиуса r > R, тогда
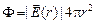 ;
; 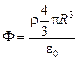 ;
;
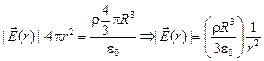 .
.
Учитывая, что полный заряд шара 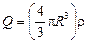 , можно представить выражение для
, можно представить выражение для  в виде
в виде
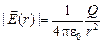 ,
,
т.е. поле такое же, как и у точечного заряда Q, помещенного в центр шара.
График показан на рис. 4.23.
СТОП! Решите самостоятельно: С4, С5, С6.
Дата добавления: 2016-04-11; просмотров: 2285;
